Содержание
- 2. Цели проекта: обеспечить компьютерную поддержку изучения свойств логарифмов и их применения в ходе преобразования выражений, содержащих
- 3. Определение логарифма Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель
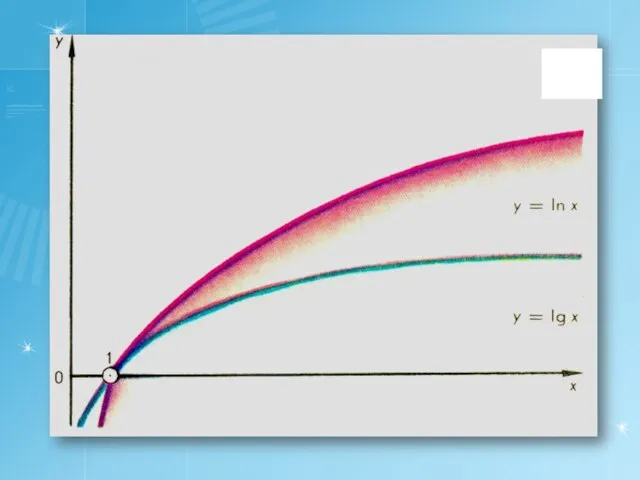
- 4. Десятичные логарифмы Если основание логарифма равно 10, то логарифм называется десятичным: Натуральные логарифмы Если основание логарифма
- 5. Свойства логарифмов, где а и в - положительны а > 0, а ≠ 1
- 6. Пример: 1) 2)
- 7. Логарифмирование алгебраических выражений Если число х представлено алгебраическим выражением, то логарифм любого выражения можно выразить через
- 8. Потенцирование логарифмических выражений Переход от логарифмического выражения к алгебраическому называется потенцированием, то есть, произвести действие, обратное
- 9. Пример: Найти X, если 1 Решение: x = 30
- 10. Частоту любого звука можно выразить формулой
- 11. Логарифмируя эту формулу, получаем
- 12. Принимая частоту самого низкого «до» за единицу n=1 и приводя логарифмы к основанию 2, имеем
- 13. Свойства монотонности логарифмов Если a > 1 и b > c, то Если 0 c, то
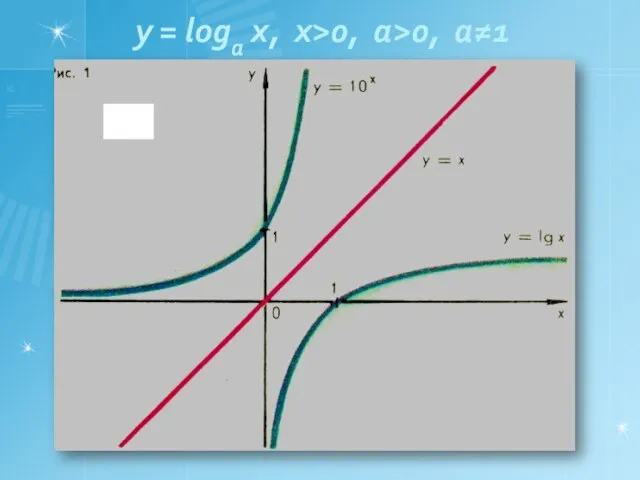
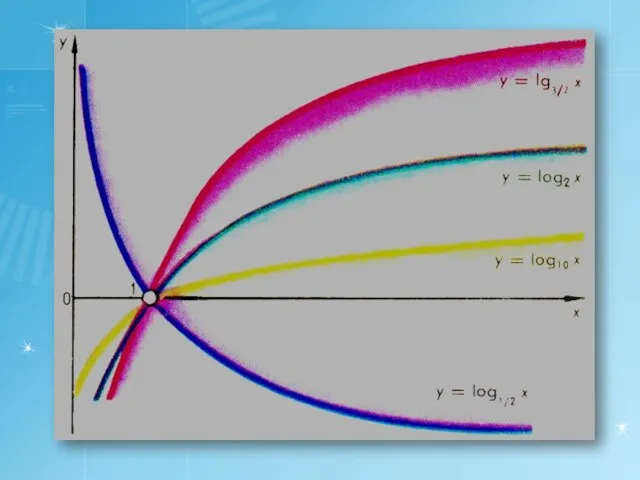
- 14. Логарифмическая функция
- 15. y = loga x, x>0, a>0, a≠1
- 18. Джон Непер Шотландский математик -изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил
- 19. Логарифмы в музыке Даже изящные искусства питаются ею Разве музыкальная гамма не есть - Набор передовых
- 20. Звезды, шум и логарифмы По вертикальной оси отложим блеск звезд в единицах Гиппарха (распределение звезд по
- 21. Логарифм шума Единица измерения децибел используется в звуковой технике. Связано это с тем, что мы реагируем
- 22. На рисунке видно, что эта спираль пересекает все прямые, проходящие через полюс под одним и тем
- 23. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им
- 24. Рога таких животных, как архары, закручены по логарифмической спирали. В подсолнухе семечки расположены по дугам, близким
- 25. По логарифмической спирали формируется и тело циклона
- 26. По логарифмическим спиралям закручены и многие галактики, в частности – Галактика Солнечной системы.
- 27. Литература Колмогоров А.Н. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. Москва. Просвещение. 2008
- 29. Скачать презентацию























 Влияние компьютерной системы с использованием sms-сообщений на контроль АД у больных артериальной гипертонией
Влияние компьютерной системы с использованием sms-сообщений на контроль АД у больных артериальной гипертонией CAREER OR FAMILY
CAREER OR FAMILY  Ремёсла восточных славян
Ремёсла восточных славян Немецкий шоколад торговой марки Lubeca (Германия)
Немецкий шоколад торговой марки Lubeca (Германия) Презентация на тему Технология моделирования в начальной школе
Презентация на тему Технология моделирования в начальной школе Светлое воскресение христово
Светлое воскресение христово М.В. Ломоносов как экономист и статистик
М.В. Ломоносов как экономист и статистик Describing people
Describing people  Дети капитана Гранта
Дети капитана Гранта Багълайыджылар
Багълайыджылар Дидактическое сопровождение и структура занятий с детьми дошкольного возраста.
Дидактическое сопровождение и структура занятий с детьми дошкольного возраста. Презентация на тему Творчество В. П. Крапивина в моем понимании «Какая–то тихая популярность!»
Презентация на тему Творчество В. П. Крапивина в моем понимании «Какая–то тихая популярность!»  Презентация на тему Образ Снегурочки в русском искусстве и литературе
Презентация на тему Образ Снегурочки в русском искусстве и литературе  Необходимые навыки для создания компании 3 волны
Необходимые навыки для создания компании 3 волны Презентация на тему Жизнь вельможи
Презентация на тему Жизнь вельможи Презентация на тему Основы безопасности жизнедеятельности 11 класс
Презентация на тему Основы безопасности жизнедеятельности 11 класс  Нормативно-правовые акты, гарантирующие право получения детям с ограниченными возможностями здоровья адекватного их возможностя
Нормативно-правовые акты, гарантирующие право получения детям с ограниченными возможностями здоровья адекватного их возможностя Фундаментальный курс по стрижкам
Фундаментальный курс по стрижкам О путях развития информационно- вычислительных систем в области внегалактических исследований
О путях развития информационно- вычислительных систем в области внегалактических исследований Леса России
Леса России МОУ Андрейковская средняя школаВяземского района Смоленской области«Внедрение инновационных образовательных проектов в практ
МОУ Андрейковская средняя школаВяземского района Смоленской области«Внедрение инновационных образовательных проектов в практ ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ СОПРОВОЖДЕНИЕ ВВЕДЕНИЯФГОС НОО
ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ СОПРОВОЖДЕНИЕ ВВЕДЕНИЯФГОС НОО Қазіргі замандағы әлемдік діндер
Қазіргі замандағы әлемдік діндер Презентация на тему Ледники
Презентация на тему Ледники  Семинар
Семинар Основы радиосвязи
Основы радиосвязи Exploring space
Exploring space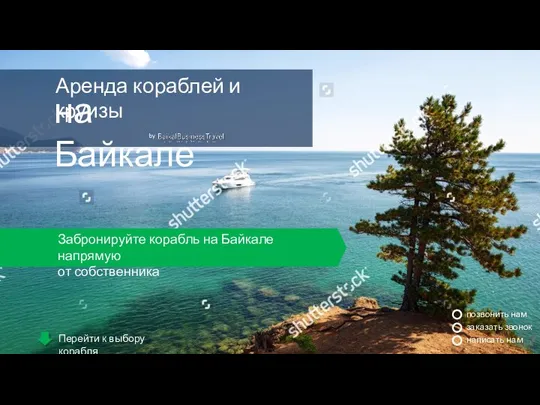 ТЗ на подготовку лендинга для круизов
ТЗ на подготовку лендинга для круизов