Логические основы работы компьютера

Логические основы работы компьютера

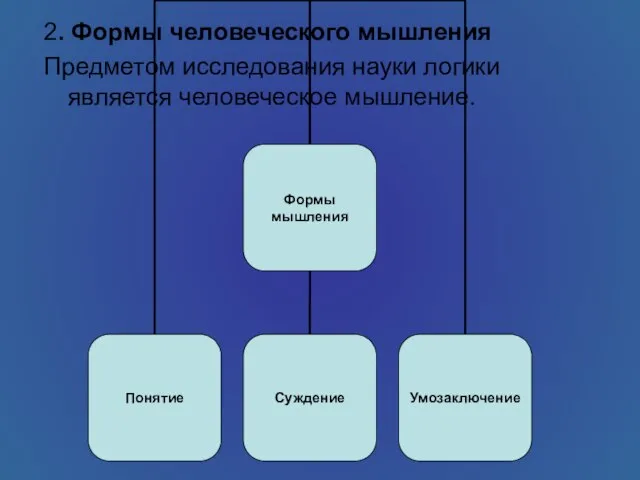
2. Формы человеческого мышления
Предметом исследования науки логики является человеческое мышление.

Понятие – форма мышления, в которой отражаются отличительные существенные признаки предметов.
Примеры понятий: апельсин, трапеция, белизна, река Нил, ураганный ветер, студент медицинского института.
Существенными называются такие признаки, каждый из которых, взятый отдельно, необходим, а все вместе достаточны, чтобы с их помощью отличить (выделить) данный предмет (явление) от всех остальных и сделать обобщение, объединив однородные предметы в множество.
Пример: апельсин – круглый, оранжевый, упругий, сладкий, ароматный.

Основные логические характеристики понятия: содержание и объём.
Содержание понятия – совокупность существенных признаков, отражённых в этом понятии.
Пример: ромб –параллелограмм, у которого все стороны равны.
Объём понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
Пример: объём понятия ученик – люди, которые когда-либо учились, учатся сейчас или будут учиться когда-нибудь.

Наглядная геометрическая иллюстрация объёмов понятий и отношений между ними была предложена математиком, физиком и астрономом
Леонардом Эйлером (1707 – 1781)
и носит название кругов Эйлера.

Суждение (высказывание, утверждение) – форма мышления, в которой что-либо утверждается или отрицается о предмета, их свойствах или отношениях между ними.
Примеры: Этот апельсин вкусный. Если пошёл дождь, то на улице весна.
Суждения бывают простыми и сложными.
Наступила весна – простое суждение.
Наступила весна, и прилетели грачи – сложное суждение.
Всякое суждение может быть истинным или ложным.
Содержание суждения – это то, о чём в нем идёт речь, его смысл.
Логическая форма суждения – это его строение, способ связи его составных частей.
Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определённым правилам вывода получаем суждение-заключение (вывод умозаключения).
Все люди смертны.
Сократ – человек.
Сократ смертен.

Основной принцип формальной логики: правильность рассуждения (умозаключения) определяется только его логической формой (структурой) и не зависит от конкретного содержания входящих в него суждений.
С точки зрения содержания, суждения, входящие в рассуждения могут быть истинными или ложными ( истинно или ложно отражать действительность), а если рассматривать рассуждение со стороны формы, то имеет значение только его логическая правильность ли неправильность.

2. Логика – наука, изучающая законы и формы мышления.
Этапы развития логики
I этап – формальная логика. Основатель – Аристотель (384 – 322 гг. до н.э.), ввел основные формы абстрактного мышления.
II этап – математическая логика. Основатель – немецкий ученый и философ Лейбниц (1642 – 1716), предпринял попытку логических вычислений.
III этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815 – 1864), ввёл алфавит, орфографию и грамматику для математической логики.

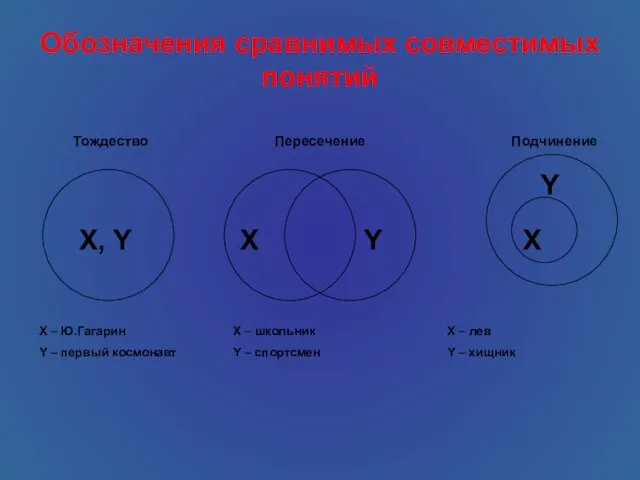
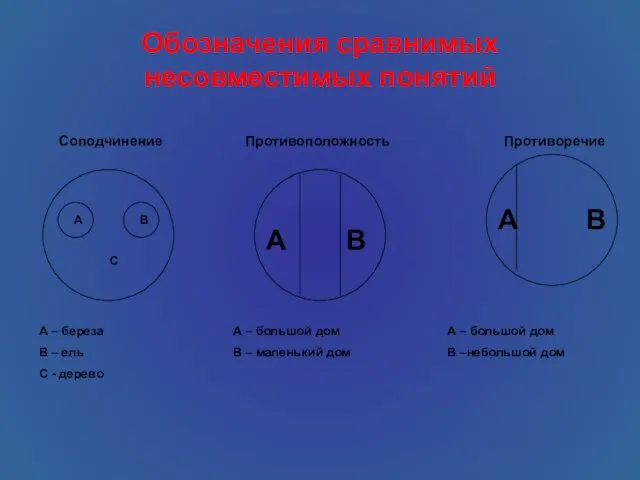
3. Отношения между понятиями
По отношению друг к другу понятия делятся на сравнимые и несравнимые.
Далёкие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми.
Несравнимые понятия: Романс и кирпич.
Сравнимые понятия делятся по объёму на совместимые (объёмы этих понятий совпадают полностью или частично) и несовместимые (объёмы которых не совпадают ни по одному элементу).

Обозначения сравнимых совместимых понятий
X, Y
X
Y
X
Y
Тождество
Пересечение
Подчинение
X – Ю.Гагарин
Y – первый космонавт
X – школьник
Y – спортсмен
X – лев
Y – хищник

Обозначения сравнимых несовместимых понятий
А
А
В
Соподчинение
Противоположность
Противоречие
А – береза
В – ель
С - дерево
А – большой дом
В – маленький дом
А – большой дом
В –небольшой дом
А
В
С
В

Понятие об алгебре высказываний

Алгебра логики – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразуют логические высказывания.
По высказыванием (суждением) будем понимать повествовательное предложение относительно которого можно сказать истинно оно или ложно.

Высказывание может принимать только оно из двух логических значений – истинно (1) или ложно (0).
Обозначать высказывания будем прописными буквами.
А = {Солнце светит для всех} = 1
В = {Все ученики любят информатику} = 0
С = {Некоторые из учеников любят информатику} = 1
D= {А ты любишь информатику?}
Е = {Посмотри в окно}
Ж = {2*x – 5 >0} – не высказывание
З = {x*x <0} = 0

Простое высказывание (логическая переменная) содержит только одну простую мысль.
А = {Квадрат – это ромб}
Сложное высказывание (логическая функция) содержит несколько простых мыслей, соединённых между собой с помощью логических операций.
F(А,В) = {Лил дождь, и дул холодный ветер}
А
В

Значение логической функции можно определить с помощью специальной таблицы .
Таблица истинности – таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.