Содержание
- 2. Логика – наука о законах и формах мышления. Слово «логика» произошло от древнегреческого logos, что означает
- 3. Логические операции. Логические операции над высказываниями выполняются на основе законов и правил булевой алгебры. Логическое умножение
- 4. Логические операции. Импликация (логическое следование) (→) соответствует связке « если …, то …» Если А, то
- 5. Построение таблиц истинности. Таблица истинности – таблица, определяющая значение сложного высказывания при всех возможных значениях простых
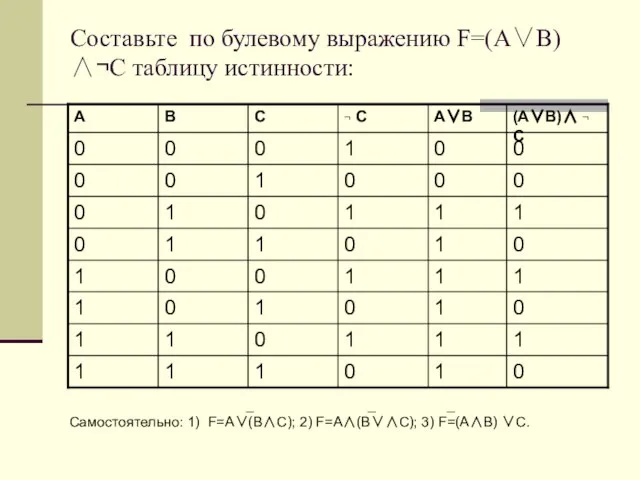
- 6. Составьте по булевому выражению F=(A∨В)∧¬C таблицу истинности: _ _ _ Самостоятельно: 1) F=A∨(В∧C); 2) F=A∧(В∨∧C); 3)
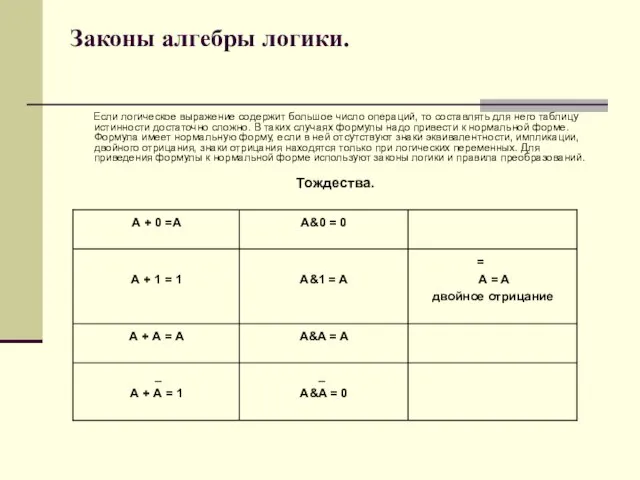
- 7. Законы алгебры логики. Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности
- 8. Законы алгебры логики. Переместительный закон А + В = В + А А & В =
- 9. Задания: 1) Записать формулу, упростить: А или (не А и В) А и (не А или
- 10. Логические схемы. Над возможностями применения логики в технике ученые и инженеры задумывались давно. Американский логик Чарльз
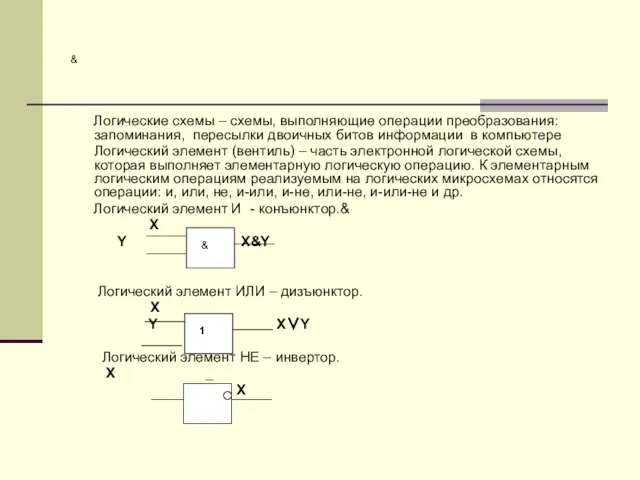
- 11. & Логические схемы – схемы, выполняющие операции преобразования: запоминания, пересылки двоичных битов информации в компьютере Логический
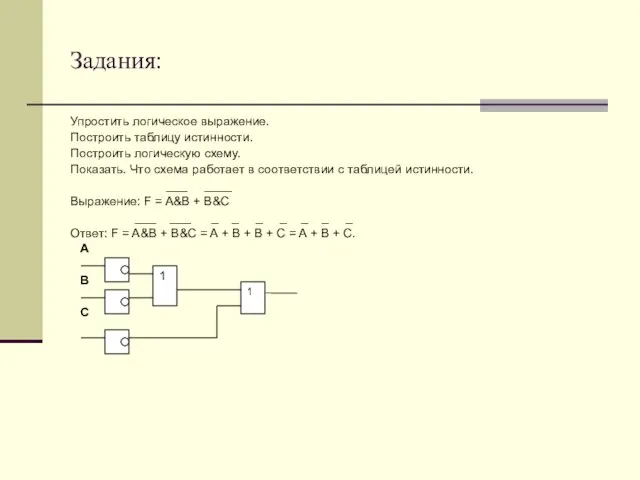
- 12. Задания: Упростить логическое выражение. Построить таблицу истинности. Построить логическую схему. Показать. Что схема работает в соответствии
- 13. Задание для самостоятельной работы: _________ _ ________ __ _____ __ 1) F = X&Y + Y&Z
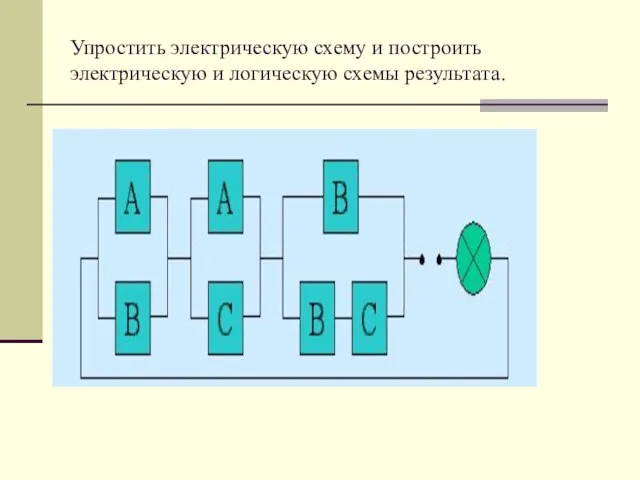
- 14. Упростить электрическую схему и построить электрическую и логическую схемы результата.
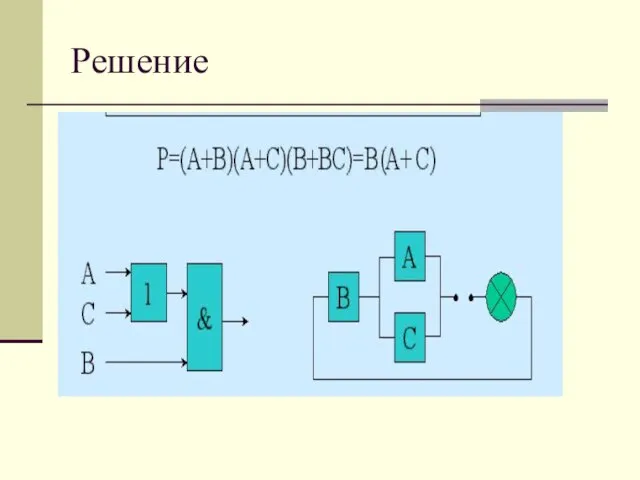
- 15. Решение
- 16. Алгебра логики дала в руки конструктора мощное средство разработки, анализа и совершенствования логических схем. Гораздо проще,
- 17. Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел. В целях максимального упрощения работы компьютера
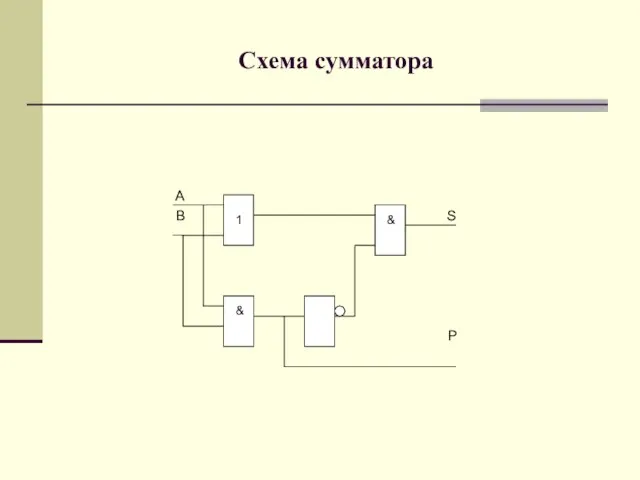
- 18. Схема сумматора A B 1 & S & P 1 & &
- 19. Триггер. Регистры. Триггер – устройство памяти компьютера для хранения одного бита информации. Это устройство позволяет запоминать,
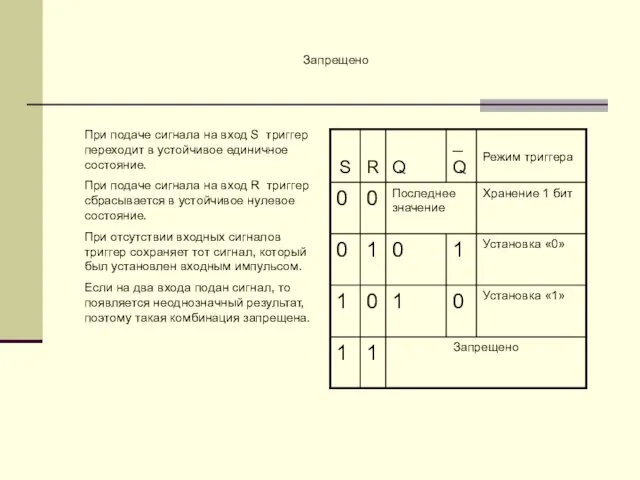
- 20. Запрещено При подаче сигнала на вход S триггер переходит в устойчивое единичное состояние. При подаче сигнала
- 22. Скачать презентацию











 Лесоразведение как альтернатива существующим практикам хозяйствования и адаптация к меняющимся климатическим условиям на приме
Лесоразведение как альтернатива существующим практикам хозяйствования и адаптация к меняющимся климатическим условиям на приме Toys, counting 1-7
Toys, counting 1-7 Формирование критического мышления в процессе обучения истории и обществознанию
Формирование критического мышления в процессе обучения истории и обществознанию Международный день образования
Международный день образования «Дело-КС» Автоматизация делопроизводства
«Дело-КС» Автоматизация делопроизводства Развитие представлений о строении атома
Развитие представлений о строении атома Теория графов
Теория графов ФУНКЦИОНАЛЬНЫЕМОДУЛИ
ФУНКЦИОНАЛЬНЫЕМОДУЛИ Откуда в нашем доме тепло?
Откуда в нашем доме тепло? Корінь. Спільнокореневі слова
Корінь. Спільнокореневі слова Дома бывают разные
Дома бывают разные ув
ув Молоко и кисломолочные продукты
Молоко и кисломолочные продукты Презентация на тему Животные Тундры
Презентация на тему Животные Тундры  ООП ФГОС ДО
ООП ФГОС ДО IX Международный семинар по проблемам ускорителей заряженных частиц памяти В.П.Саранцева
IX Международный семинар по проблемам ускорителей заряженных частиц памяти В.П.Саранцева Управление рисками и контроль выполнения политики безопасности с помощью системы ІР-Guard
Управление рисками и контроль выполнения политики безопасности с помощью системы ІР-Guard Подготовка к сочинению-рассуждению ОГЭ 2016
Подготовка к сочинению-рассуждению ОГЭ 2016 Какие изменения ждут ребенка в 1 классе?
Какие изменения ждут ребенка в 1 классе? ТРЕБОВАНИЯК СТРУКТУРЕ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
ТРЕБОВАНИЯК СТРУКТУРЕ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ Су құбырлы электржетегтерді ауылшаруашылығында пайдыланылуы (водопровод с элетроприводом)
Су құбырлы электржетегтерді ауылшаруашылығында пайдыланылуы (водопровод с элетроприводом) Возможности систем «Трактиръ»
Возможности систем «Трактиръ» Презентация на тему Методы исследования в биологии
Презентация на тему Методы исследования в биологии  Микробиоценоз полости рта. Препараты БактоБЛИС и ДентобЛИС
Микробиоценоз полости рта. Препараты БактоБЛИС и ДентобЛИС Я выбираю здоровый образ жизни
Я выбираю здоровый образ жизни Право. Основные понятия
Право. Основные понятия Фигурное катание
Фигурное катание B2B TRANS
B2B TRANS