Содержание
- 2. ПРОБЛЕМА СКРЫТОЙ ИЛИ ТЕМНОЙ МАССЫ ВОЗНИКЛА ИЗ-ЗА CИЛЬНОГО РАССОГЛАСОВАНИЯ ПРЯМЫХ И КОСВЕННЫХ ОЦЕНОК МАССЫ ГАЛАКТИК (и
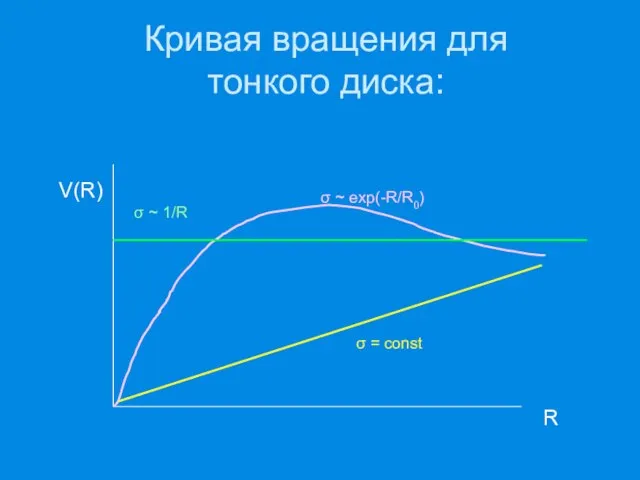
- 3. Кривая вращения для тонкого диска: σ = const σ ~ 1/R σ ~ exp(-R/R0) R V(R)
- 4. Два (исторически) главных аргумента в пользу существования DM в дисковых галактиках: Отношение массы к светимости M/L
- 5. Высокие M/LB в пределах оптического диска Рекордсмены UGC 3303, dIrr, M/LB = 31, Караченцев и др.
- 6. Насколько надежна фотометрическая оценка массы звездного населения?
- 7. ПРОБЛЕМА оценки массы звездного населения по данным фотометрии (яркость + цвет) Оценка чувствительна к функции масс
- 8. ПРОБЛЕМА оценки массы по измерениям скоростей вращения диска Неопределенность самого понятия «масса галактики» Не-круговые движения Необходимость
- 9. МАССА ТЕМНОГО ВЕЩЕСТВА = ДИНАМИЧЕСКИ ОПРЕДЕЛЕННАЯ МАССА – МАССА ЗВЕЗДНОГО НАСЕЛЕНИЯ – МАССА ГАЗА. Чтобы понять,
- 10. ПРЕИМУЩЕСТВА, КОТОРЫЕ ДАЕТ ОЦЕНКА СКОРОСТЕЙ СТАРОГО ЗВЕЗДНОГО НАСЕЛЕНИЯ ДИСКА Сводятся к минимуму влияние некруговых скоростей, связанных,
- 11. Гипотеза об устойчивости: Звездный (звездно-газовый) диск должен быть устойчив к гравитационным возмущениям в плоскости диска и
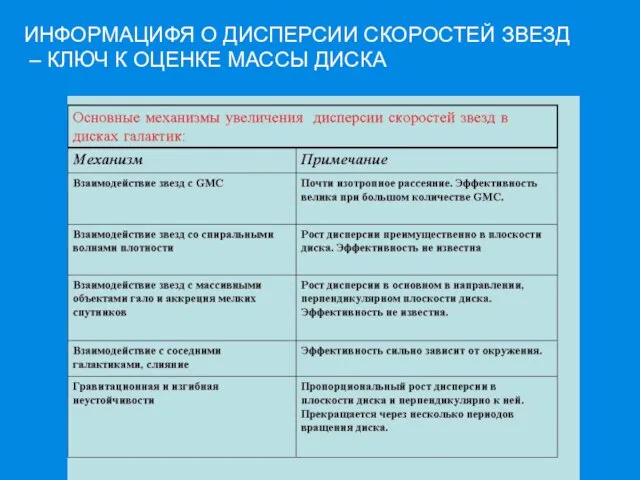
- 12. ИНФОРМАЦИФЯ О ДИСПЕРСИИ СКОРОСТЕЙ ЗВЕЗД – КЛЮЧ К ОЦЕНКЕ МАССЫ ДИСКА
- 13. Дисперсия скоростей звезд диска + кривая вращения (исправленная за асимметричный дрейф) дает возможность оценить : --
- 14. ЧИСЛЕННЫЕ 3D-MOДЕЛИ Диск: N = 20·103 - 100·103, газ не учтен Гало и балдж (не эволюционирующие)
- 15. НАБЛЮДЕНИЯ: BTA, 6m reflector of Special Astrophysical Observatory, Russian Academy of Sciences Device: SCORPIO, long slit
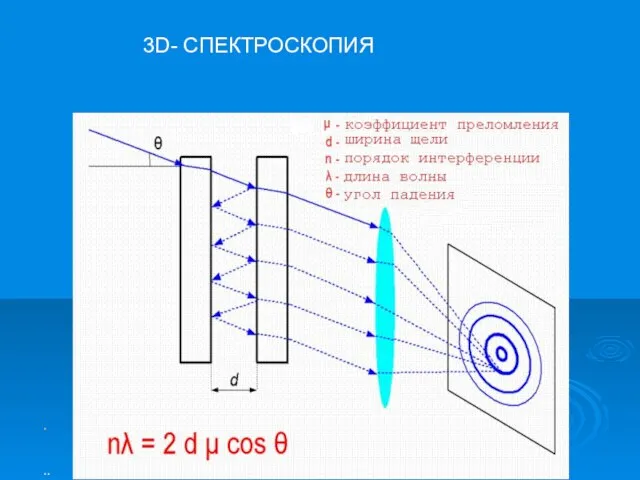
- 16. . .. . 3D- СПЕКТРОСКОПИЯ
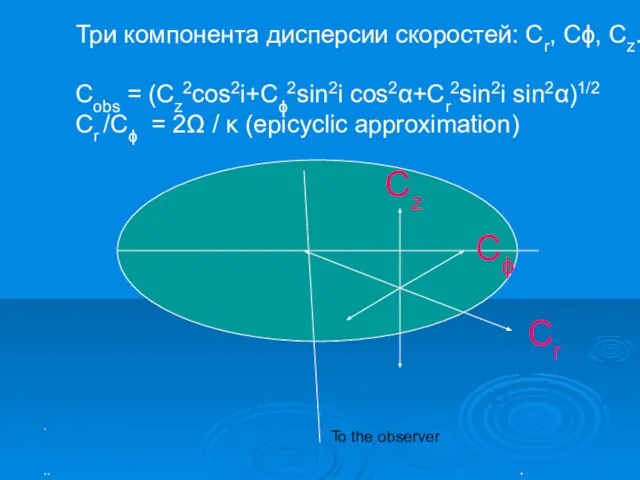
- 17. . .. . Три компонента дисперсии скоростей: Cr, Cϕ, Cz. Cobs = (Cz2cos2i+Cϕ2sin2i cos2α+Cr2sin2i sin2α)1/2 Cr
- 18. . .. .
- 19. ПРОБЛЕМА С ДИСКАМИ ГАЛАКТИК НИЗКОЙ ЯРКОСТИ (LSB- галактик) Принято считать: темная масса доминирует почти от самого
- 20. MAXIMUM DISK AGAINST SUBMAXIMUM DISK: WHO WINS? Let L be disc radial scalelength. Maximum disk :
- 21. To connect the velocity dispersion with the local density of a disc, one may either a)
- 22. NUMERICAL 3D-MODELS of marginally stable discs TREEcode method Disc: N = 2·105 - 106 , no
- 23. NUMERICAL 3D-MODELS Disc: N = 2·105 - 106 , no gas A wide range of radial
- 24. Чтобы связать дисперсию скоростей звезд с плотностью диска, необходимо либо а) считать известным параметр устойчивости Q
- 25. Analytical local criteria of threshold values of radial velocity dispersion Cr: Toomre’ criterion QT = 1,
- 26. AHAЛИТИЧЕСКИЕ локальные критерии устойчивости (пороговые значения радиальной дисперсии скоростей звезд Cr): Let Q = Cr /(Cr)TOOMRE
- 27. , Let Cobs – observed velocity dispersion (LOSVD) Cmin - line-of sight velocity dispersion, expected for
- 28. The example: NGC 4150 – So/a galaxy with a very small disc and practically no bulge
- 30. Скачать презентацию






















 Контрактное производство
Контрактное производство Тригонометрия
Тригонометрия Московский лабиринт
Московский лабиринт Деятельностный подход на современном уроке по развитию речи обучающихся с НОДА и УО
Деятельностный подход на современном уроке по развитию речи обучающихся с НОДА и УО Презентация "Устройство храмов" - скачать презентации по МХК
Презентация "Устройство храмов" - скачать презентации по МХК Главные герои новогоднего праздника – это Дед Мороз и Снегурочка
Главные герои новогоднего праздника – это Дед Мороз и Снегурочка Владимир Вольфович Жириновский
Владимир Вольфович Жириновский Нобелевские лауреаты
Нобелевские лауреаты Венгерский язык
Венгерский язык От качества образования к качеству жизни: стратегия и перспективы
От качества образования к качеству жизни: стратегия и перспективы Нина Хаген
Нина Хаген ПУТЕШЕСТВИЕ В МИР ОПАСНОСТЕЙ
ПУТЕШЕСТВИЕ В МИР ОПАСНОСТЕЙ Красная книга Ленинградской области
Красная книга Ленинградской области Составь схему слова
Составь схему слова Болгария
Болгария МЕТОД ЗАМЕНЫ ФУНКЦИИ
МЕТОД ЗАМЕНЫ ФУНКЦИИ Тема любви в повести А.И. Куприна "Гранатовый браслет"
Тема любви в повести А.И. Куприна "Гранатовый браслет" Презентация на тему: Обезьянка-воровка
Презентация на тему: Обезьянка-воровка Поле чудес на английском
Поле чудес на английском Организация бизнеса
Организация бизнеса Самозавязывающиеся шнурки
Самозавязывающиеся шнурки Люди, отданные науке
Люди, отданные науке ВЫЗОВ КАРДИОЛОГУ ?!
ВЫЗОВ КАРДИОЛОГУ ?! Восстание Спартака (6 класс)
Восстание Спартака (6 класс) Философия, её смысл, функции и роль в обществе
Философия, её смысл, функции и роль в обществе Романтический балет в трех действиях с эпилогом Корсар
Романтический балет в трех действиях с эпилогом Корсар Сырный сервис
Сырный сервис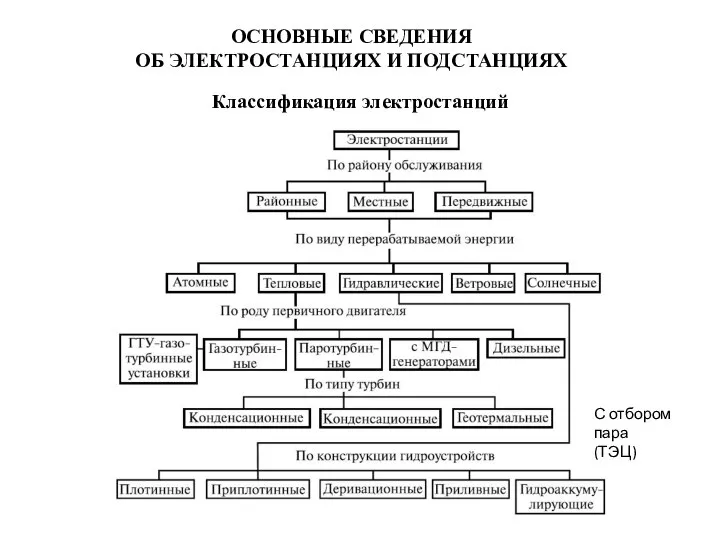 Электростанции и подстанции. Классификация электростанций с отбором пара (ТЭЦ)
Электростанции и подстанции. Классификация электростанций с отбором пара (ТЭЦ)