Мастер – класс «Нестандартный подход в совершенствовании вычислительных навыков у младшего школьника. Подготовка к олимпиаде по

Информационная справка
В 1967 году детский сад № 48 «Дружная семейка» принял своих первых воспитанников.
В 2000г. МОУ аккредитовано в статусе муниципального образовательного учреждения для детей дошкольного и младшего школьного возраста начальная школа – детский сад № 48.
В 2004г. МОУ НШДС № 48 при повторной аттестации подтвердило свой статус и прошло аккредитацию. Учредителем выступает мэрия городского округа Тольятти
для детей с 3 до 11 лет.
На сегодняшний день наше учреждение (НШДС № 48) имеет
4 начальных класса и 6 дошкольных групп,
125 воспитанника и 94 учеников.
Количество учащихся в школе и воспитанников в детском саду в течение последних трех лет остается стабильным.

Наши достижения.
1994-1995 уч. г.– 3 – е место в районной олимпиаде по математике
Ахмеджанов Руслан.
1995-1996 уч. г. – 2-е место в районной олимпиаде по математике
Макитрина Таня.
1996-1997 уч. г. – 1-е место в городской олимпиаде по математике
Родомакина Кристина.
1998-1999 уч. г. – 2-е и 3-е места в районной олимпиаде по математике и
русскому языку
Кириенко Света, Торопова Аня
2003-2004 уч. г. – 2-е место в городской олимпиаде по математике
Гладков Илья
2004-2005 уч. г. – 2-е место в районной олимпиаде по русскому языку
Бочагова Алина, Янина Ксения.
2005-2006 уч. г. – 1-е командное место по математике и три первых
места в личном зачёте
Девяткин Никита, Гришин Юра, Куликов Саша.
2-е командное место по русскому языку и первое личное
место - Гришин Юра

Наши достижения
2006-2007 уч. г. – Призёры городской олимпиады по математике и русскому языку – Щеглов Георгий, Петрова Алина,
Бабушев Буба.
2007-2008 уч. г. – Дипломы I, II, III степени в областном конкурсе
«Скажем терроризму – нет!» - Рудник Катя, Петрова
Алина, Янина Кристина.
2008-2009 уч. г. – Призёры городской олимпиады по русскому языку и
математике – Лопатин Дима, Рудник Катя.
2-е место по городу, 4-е место в регионе
в Международной математической игре «Кенгуру - 2009»
2008-2009 уч. г. – Диплом III степени за успехи в области русского языка,
математики, литературы и Интернет – технологий,
достигнутые на Межрегиональной дистанционной
олимпиаде «Нескучная зима».

Наши достижения
2009-2010 уч. г. – 2-е место в районной олимпиаде по математике и
русскому языку – Тараканов Кирилл, Челышева Настя.
2-е место в регионе «Кенгуру - 2010»,
2-е место в Международной игре «Русский медвежонок»
Лауреаты Всероссийского конкурса
«Познание и творчество»
в номинации «В царстве математики» - Артемьев Дима,
Китёв Матвей.
2010 – 2011 уч. г. – МОУ НШДС № 48 присвоено звание ЛАУРЕАТ Российского
заочного конкурса «Познание и творчество» в
номинации «Начальная школа» по итогам 2010-2011уч.г.
18 учащихся получили звание ЛАУРЕАТ Российского
заочного конкурса «Познание и творчество» в
номинации «Лингвистические игры», «Экзамен по
русскому языку», «Окружающий мир».
2-е место в районной олимпиаде по русскому языку
Горбат Софья.

Математика – это язык, на котором написана природа.
Важнейшая задача школы – давать подрастающего поколению глубокие и прочные знания.

Многое зависит от учителя:
как организует внеклассную работу;
какие формы внеклассной работы предлагает детям;
учет уровня подготовленности класса, их интересы, индивидуальные и возрастные особенности каждого ученика,
Итог: Высокий результат

Цель проведения математической олимпиады:
Через выполнение различных работ сильными учащимися помочь учителю осознать программный материал,
разбудить в нем желание к творчеству на каждом уроке,
склонить учителя к тому, что внеклассная работа – это один из важных путей проведения содержательной и интересной работы с учащимися начальных классов.
Олимпиада – не только итог внеклассной работы за год, но и прекрасный стимул для развертывания внеклассной работы.

Для успешного проведения олимпиады необходимо:
Систематическое проведение всей внеклассной работы по математике.
Обеспечение регулярности проведения олимпиады.
Серьезная содержательная подготовка перед проведением олимпиады.
Правильная организация проведения олимпиад.
Интересное математическое содержание заданий.

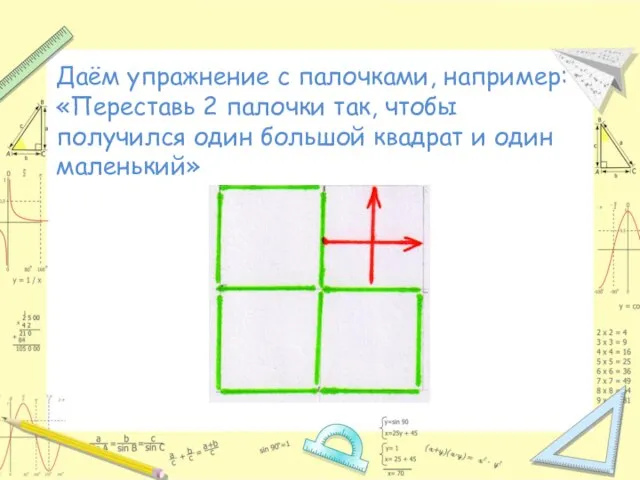
Даём упражнение с палочками, например: «Переставь 2 палочки так, чтобы получился один большой квадрат и один маленький»

Работа над олимпиадными задачами:
Задача № 1
«На двух полках стояли 12 книг. Когда с первой полки на вторую переставили столько книг, сколько до этого стояло на второй полке, то книг на полках стало поровну. Определите, сколько книг первоначально стояло на каждой полке?»

Задача № 2
«В синей коробке было в три раза больше шариков, чем в красной. Когда в красную коробку положили ещё 14 шариков, тогда в обеих коробках их стало поровну. Сколько шариков в синей коробке?»
3х = х + 14
3х – х = 14
2х = 14
х = 14 : 2
х = 7 7 шариков в красной коробке, а в синей – в три раза больше. 7х3 = 21 (шарик)

А можно решить ещё проще:
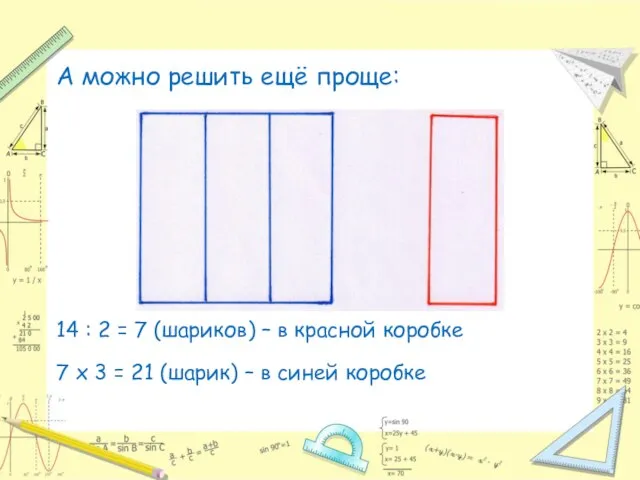
14 : 2 = 7 (шариков) – в красной коробке
7 х 3 = 21 (шарик) – в синей коробке

Задача № 3
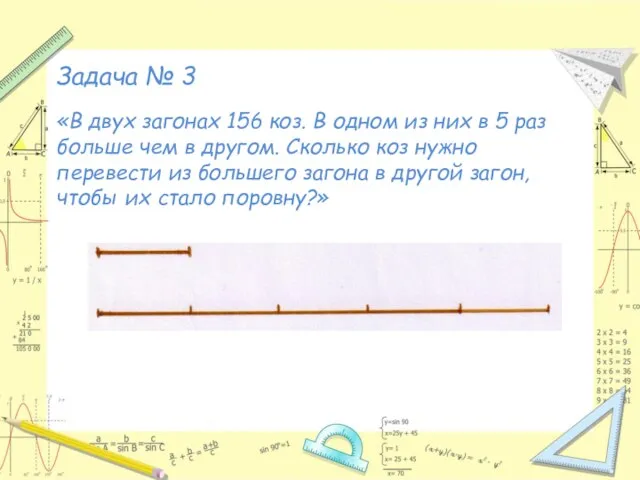
«В двух загонах 156 коз. В одном из них в 5 раз больше чем в другом. Сколько коз нужно перевести из большего загона в другой загон, чтобы их стало поровну?»

Решение:
1 способ:
1+5 = 6 (частей) – всего
156 : 6 = 26 (коз) – в 1 загоне (или 1 часть)
156 : 2 = 78 (коз) – должно быть в каждом загоне
78 – 26 = 52 (козы)
2 способ:
1) 1+ 5 = 6 (частей) – всего
2) 156 : 6 = 26 (коз) – в 1 загоне (или 1 часть)
3) 26 х 5 = 130 (коз) – в 2 загоне
4) 156 : 2 = 78 (коз) - должно быть в каждом загоне
5) 130 – 78 = 52 (козы)

3 способ:
Глядя на краткую запись, мы видим, что всего 6 частей. А нам надо их разделить поровну, т.е. по 3.
Значит, нужно к одной части прибавить ещё 2 части. Таким образом решение задачи будет совсем простым:
1) 1 + 5 = 6 (частей) – всего
2) 156 : 6 = 26 (коз) – в 1 загоне (или 1 часть)
3) 26 х 2 = 52 (козы)

Задача № 4
«3 утёнка и 4 гусёнка весят 2500 г, а 4 утёнка и 3 гусёнка весят 2400 г. Сколько весит 1 гусёнок?»
3 утёнка и 4 гусёнка – 2 кг 500 г
4 утёнка и 3 гусёнка – 2 кг 400 г
Почему в первой строке больше?
Потому что гусь тяжелее утки.

Решение:
3 + 4 + 4 + 3 = 14 (птиц) – всего
2 кг 500 г + 2 кг 400 г = 4 кг 900 г – масса 14 птиц
4 кг 900 г : 14 = 350 г – масса 1 птички при одинаковом весе
2 кг 500 г – 2 кг 400г = 100 г – на столько тяжелее гусята
100 : 2 = 50 (г) – на столько тяжелее 1 гусёнок
350 + 50 = 400 (г) – масса 1 гусёнка

Задание № 5
«Если в некотором трехзначном числе, оканчивающемся 0, отбросить этот 0, то число уменьшится на 351. Найдите это число».
ХХ0
- ХХ
3 5 1

Решение:
Х 9 0
- Х 9
3 5 1

3 9 0
- 3 9
3 5 1
Итак, это число 390

Задача № 6
«Наша футбольная команда провела 31 матч, 7 из них вничью. При этом команда набрала 64 очка (по 3 очка за победу, по 1 очку за ничью и 0 очков за поражение). Сколько матчей команда проиграла?»
31 – 7 = 24 (матча) – победа и поражение
64 – 7 = 57 (очков) – за победу
57 : 3 = 19 (матчей) – победа
24 – 19 = 5 (матчей) - поражение

Обучение нетрадиционным
вычислительным навыкам
Возведение в квадрат двузначных чисел, оканчивающихся на «5».
Например: 352
В этом числе 3 десятка. Умножаем цифру 3 на следующую цифру, т.е. 4 и приписываем 25.
Получаем: 352 = 3 х 4 и приписываем 25, получаем 1225.
152 = 1 х 2 и приписываем 25, получаем 225
252 = 625 652 = 4225
352 = 1225 752 = 5625
452 = 2025 852 = 7225
552 = 3025 952 = 9025

Этим же способом можно возводить в квадрат и трёхзначные числа, оканчивающиеся на «5».
Например: 1352
Число десятков умножаем на следующее число и приписываем к нему 25.
13 х 14 и приписываем 25
А вот как можно умножить двузначные числа, если число десятков равно 1.
13 х 14
К первому числу прибавляем единицы второго числа и умножаем на 10
(13 + 4) х 10 = 170

Теперь перемножаем единицы обоих чисел
3 х 4 = 12
И к 170 прибавляем 12, получилось 182
13 х 14 = 182

Итак, 1352
13 х 14 = 182 и приписываем 25, получилось 18225.
1852 = 18 х 19 и приписываем 25
18 х 19 = (18 + 9) х 10 = 270
8 х 9 = 72
270 + 72 = 342 и приписываем 25, получаем 34225