Содержание
- 2. Содержание Введение Генеральная совокупность и выборка Способы отбора Статистическое распределение выборки Эмпирическая функция распределения Статистические оценки
- 3. Введение Математическая статистика – наука, занимающаяся методами обработки экспериментальных данных, полученных в результате наблюдений над случайными
- 4. Генеральная совокупность и выборка Полный набор всех возможных значений дискретной СВ называется генеральной совокупностью. N –
- 5. Способы отбора Отбор, не требующий расчленения: простой, бесповторный с повторениями Отбор, при котором вся генеральная совокупность
- 6. Статистическое распределение выборки Пусть из генеральной совокупности извлечена выборка, причем значение x1 встречалось n1 и т.д.,
- 7. Эмпирическая функция распределения Эмпирической функцией распределения (функция распределения выборки) называетсяF*(x), определяющую для каждого значения xотносительную частоту
- 8. Статистические оценки параметров распределения Точечные оценки Интервальные оценки Точность и надежность Доверительный интервал для мат.ожидания Доверительный
- 9. Для того, чтобы статистические оценки давали хорошее приближение оценивающих параметров, они должны удовлетворять условиям: объем выборки
- 10. Точечные оценки Точечной называют оценку, определяющую одним числом. Пусть требуется изучить количественный признак генеральной совокупности. Допустим,
- 11. Генеральная и выборочная средняя Генеральная средняя – среднее арифметическое значений генеральной совокупности – с повторениями Генеральная
- 12. Генеральная и выборочная дисперсии Генеральной дисперсией называют среднее арифметическое квадратов отклонений значений генеральной совокупности от их
- 13. Интервальные оценки Интервальной оценкой называют оценку, определяющуюся двумя концами интервала. При выборке малого объема точечная оценка
- 14. Точность и надежность Пусть найденная по данной выборке статистическая характеристика θ* служит оценкой неизвестного параметра θ
- 15. Доверительный интервал для мат.ожидания Рассмотрим нахождение доверительного интервала для M(X) нормально распределенной СВ, т.е. нужно найти
- 16. Расчет доверительных интервалов при известной дисперсии Будем рассматривать выборочную среднюю как случайную величину. Примем без доказательств,
- 17. Расчет доверительных интервалов при неизвестной дисперсии Если D(x) неизвестна, а ее несмещенная оценка S2, то в
- 18. Доверительный интервал для оценки дисперсии Доверительный интервал строится на основании того, что величина (n–1)S2/σ распределена по
- 19. Проверка статистических гипотез Статистической гипотезой называют, гипотезу о видах неизвестного распределения или о параметрах известного распределения.
- 20. Классификация гипотез Статистические, нестатистические Выдвинутая, конкурирующая. Выдвинутую гипотезу называют нулевой (основной) и обозначают Н0. Конкурирующая гипотеза
- 21. Статистический критерий, статистическая область Для проверки Н0, используют специально подобранную слу-чайную величину, точное или приближенное значение
- 22. Критической областью называют, совокупность значений критерия при которых Н0 отвергается. Областью принятия гипотезы (областью допустимых значений),
- 23. Правостороннюю называют критическую область определяемую неравенством К>Ккр Левостороннюю называют критическую область определяемую неравенством К Двустороннюю называют
- 24. Сравнение двух дисперсий Рассмотрим гипотезу о параметрах нормального распределе-ния. Пусть имеется две серии опытов, регистрирующая значение
- 25. Механизм проверки По данным выборок значений nх и nу, вычисляют наблюдаемое значение критерия как отношение большей
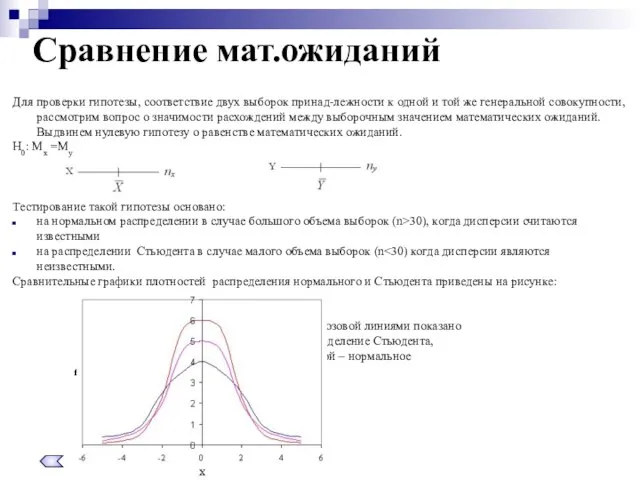
- 26. Для проверки гипотезы, соответствие двух выборок принад-лежности к одной и той же генеральной совокупности, рассмотрим вопрос
- 27. Для того чтобы при заданном уровне значимости α =0.05 проверить нулевую гипотезу Н0: Мх=Му о равенстве
- 28. Проверка гипотезы о равенстве средних при неизвестных дисперсиях Постановка задач: пусть генеральные совокупности распределены нормально, причем
- 29. Алгоритм проверки 1) Прежде чем сравнивать средние требуется проверить Н0: Dх=Dу 2) Если гипотеза подтвердилась нужно
- 30. Проверка гипотезы о законе распределения генеральной совокупности Если закон распределения не известен, но есть основание предположить,
- 31. Критерий Пирсона Пусть по выборке объема n получены эмпирические частоты, т.е. мы имеем предполагаемое распределение. Допустим,
- 32. Правила проверки Для того, чтобы при заданном уровне значимости α проверить Н0: “генеральная совокупность распределена нормально”,
- 33. Корреляционно-регрессионный анализ Корреляционная зависимость Корреляционный момент Коррелированность и зависимость случайных величин Выборочное корреляционное отношение Простейшие случаи
- 34. Во многих задачах требуется установить или оценить зависимость изучаемо случайной величины Y от одной или нескольких
- 35. Корреляционная зависимость Предположим изучается связь между случайными величинами Х и Y. Пусть каждому значению Х соответствует
- 36. Коэффициент корреляции. Выборочным коэффициентом корреляции называется отношение разности между М(Х) произведения случайных величины и произведением математических
- 37. Корреляционный момент Корреляционным моментом μху случайных величин Х и Y, называют математическое ожидание при отклонении этих
- 38. Коррелированность и зависимость случайных величин Две случайных величин называются коррелированными, если их корреляционный момент (или что
- 39. Выборочное корреляционное отношение Для оценки тесноты нелинейной корреляционной связи служат такие характеристики как: выборочное корреляционное отношение
- 40. Достоинства корреляционного отношения. Корреляционное отношение служит мерой тесноты связи любой, в том числе и линейной. В
- 41. Простейшие случаи криволинейной корреляции Если график регрессии Y на Х изображен кривой линией, то корреляция называется
- 42. Метод наименьших квадратов Метод наименьших квадратов заключается в том, что сумма квадратов отклонений теоретических данных от
- 43. Для того чтобы найти погрешность данного метода необходимо вычислить Если предположили нелинейную корреляцию, то уравнение связи
- 44. Если нужно отобрать 20% изготовленных деталей, то отбирают каждую пятую. Детали изготавливаются на разных станках. Выборка
- 45. Задано распределение частот выборки. Определить объем, написать распределение относительных частот. n=3+10+12=20 Σ Wi=1 Σ ni=n
- 46. Пусть имеется нормальное распределение. Тогда нужно оценить, найти M(x) и σ. Для показательного распределения нужно оценить
- 47. Найти доверительный интервал с надежностью 0.9 неизвестного M(X) нормально распределенной СВ Х, если известны =20.9, σ=2,
- 48. По данным выборки, объема 50, найдена =-0.155, S=936. Найти доверительный интервал для неизвестной дисперсии, β=0.95. n=50,
- 49. При доверительной вероятности 90% найти доверительный интервал для D(x), если для выборки, объемом 5 выборочная D(x)=6.6,
- 50. Если Н0 состоит в предположении, что математическое ожидание М(Х) нормального распределения равно 10, то Н1 может
- 52. Скачать презентацию
















































 Вскармливание детей
Вскармливание детей warm_up
warm_up Teaching speaking skills
Teaching speaking skills  Великие математики
Великие математики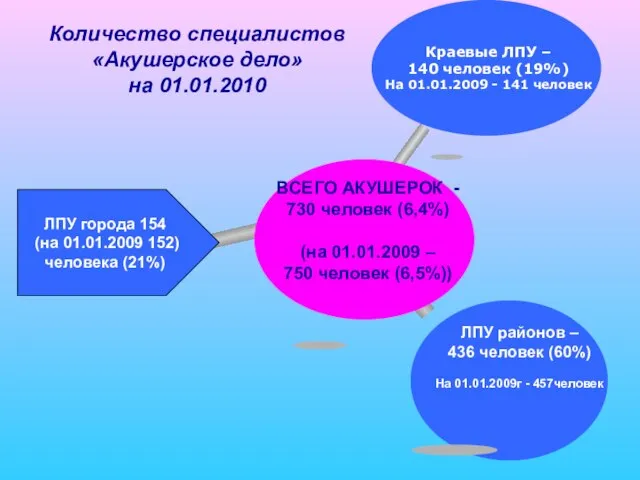 Количество специалистов «Акушерское дело» на 01.01.2010
Количество специалистов «Акушерское дело» на 01.01.2010 Презентация на тему Нахождение числа по его дроби
Презентация на тему Нахождение числа по его дроби  Рофориетация в начальной школе
Рофориетация в начальной школе Художественная культура Античности
Художественная культура Античности Презентация англ.яз
Презентация англ.яз РМЦ УЧИТЕЛЕЙ ХИМИИ
РМЦ УЧИТЕЛЕЙ ХИМИИ Презентация на тему Омонимы 3 класс
Презентация на тему Омонимы 3 класс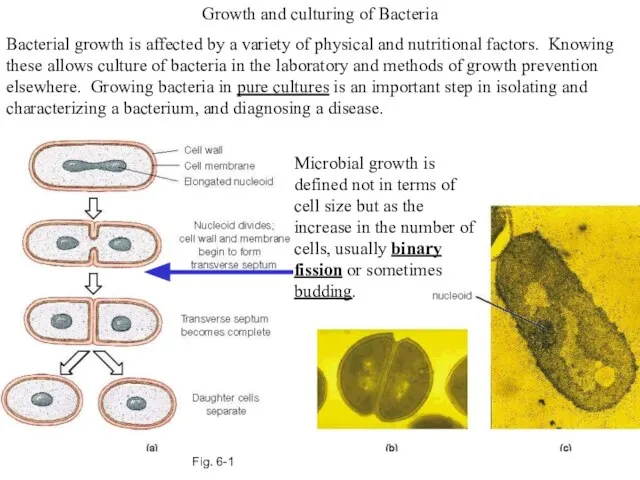 Growth and culturing of Bacteria
Growth and culturing of Bacteria НАНОТЕХНОЛОГИИна службе здоровья
НАНОТЕХНОЛОГИИна службе здоровья Народная архитектура Вожегодского края
Народная архитектура Вожегодского края Налог на профессиональный доход
Налог на профессиональный доход Нам нужны союзники!
Нам нужны союзники! Уроки на основе системно-деятельностного подхода на уровне НОО
Уроки на основе системно-деятельностного подхода на уровне НОО Инструктаж по поведению на льду
Инструктаж по поведению на льду От теории до прикладных исследований всего лишь шагФ. Алескеров НИУ ВШЭЗвенигород27.05.2012
От теории до прикладных исследований всего лишь шагФ. Алескеров НИУ ВШЭЗвенигород27.05.2012 A la d couverte de la Belgique. Auto-test
A la d couverte de la Belgique. Auto-test Проведение ГИА 2021 с использованием механизма демонстрационного экзамена, защиты ВКР и оценки квалификаций
Проведение ГИА 2021 с использованием механизма демонстрационного экзамена, защиты ВКР и оценки квалификаций Презентация на тему Изделия из драгоценных металлов
Презентация на тему Изделия из драгоценных металлов Кто такой PR-специалист?
Кто такой PR-специалист? Спортивный туризм. Основы физической подготовки
Спортивный туризм. Основы физической подготовки Муниципальное общеобразовательное учреждение«Парбигская средняя общеобразовательная школа»Детская организация «Республика
Муниципальное общеобразовательное учреждение«Парбигская средняя общеобразовательная школа»Детская организация «Республика  Политическая сфера
Политическая сфера Лыжная подготовка дошкольника
Лыжная подготовка дошкольника Гидросфера и проблемы загрязнения водной среды
Гидросфера и проблемы загрязнения водной среды