Слайд 2 Основы современного понимания информации были заложены Клодом Шенноном в работе «Математическая

теория связи» . Под информацией Шеннон понимал только те передаваемые сообщения, которые уменьшают неопределенность у получателя информации. Таким образом, информация измеряется разностью энтропий системы до и после получения информации, а сама информация выступает как мера отношения и взаимосвязи между системами, явлениями и процессами.
Слайд 3 На сегодняшний день все системы цифровой связи проектируются на основе фундаментальных

принципов и законов передачи информации, разработанных Шенноном. В соответствии с теорией информации вначале из сообщения устраняется избыточность, затем информация кодируется при помощи кодов, устойчивых к помехам, и лишь потом сообщение передается по каналу потребителю. Значительно была сокращена избыточность телевизионных, речевых и факсимильных сообщений, именно благодаря теории информации.
Слайд 4 Шеннон первым начал рассматривать передаваемые сообщения и шумы в каналах связи

с точки зрения статистики, рассматривая как конечные множества сообщений, так и непрерывные множества сообщений. Развитая Шенноном теория информации помогла решить главные проблемы, связанные с передачей сообщений, а именно: устранить избыточность передаваемых сообщений, произвести кодирование и передачу сообщений по каналам связи с шумами. Решение проблемы избыточности подлежащего передаче сообщения позволяет максимально эффективно использовать канал связи.
Слайд 5 Современные повсеместно используемые методы снижения избыточности в системах телевизионного вещания на

сегодняшний день позволяют передавать до шести цифровых программ коммерческого телевидения, в полосе частот, которую занимает обычный сигнал аналогового телевидения. Решение проблемы передачи сообщения по каналам связи с шумами при заданном соотношении мощности полезного сигнала к мощности сигнала помехи в месте приема, позволяет передавать по каналу связи сообщения со сколь угодно малой вероятностью ошибочной передачи сообщения. Также, это отношение определяет пропускную способность канала. Это обеспечивается применением кодов, устойчивых к помехам, при этом скорость передачи сообщений по данному каналу должна быть ниже его пропускной способности
Слайд 6 Шеннон задался простой целью: улучшить процесс передачи информации по телеграфному или

телефонному каналу, находящемуся под воздействием электрических возмущений или шума. Он пришел к выводу, что наилучшее решение заключается не в техническом усовершенствовании линий связи, а в более эффективной упаковке информации.
Слайд 7 Что такое информация? Оставляя в стороне вопрос о содержании этого понятия,

Шеннон показал, что это измеримая величина: количество информации, содержащейся в данном сообщении, есть функция вероятности, что из всех возможных сообщений будет выбрано данное. Он назвал общий потенциал информации в системе сообщений как ее “энтропию”. В термодинамике это понятие означает степень случайности (или, если угодно, “перемешанности”) системы. (Однажды Шеннон сказал, что понятием энтропии ему посоветовал воспользоваться математик Джон фон Нейман, указавший, что, т. к. никто не знает, что это такое, у Шеннона всегда будет преимущество в спорах, касающихся его теории.)
Слайд 8
Шеннон определил основную единицу количества информации, названную потом битом, как

сообщение, представляющее один из двух вариантов: например, “орел” — “решка”, или “да” — “нет”. Бит можно представить как или 0, или как присутствие или отсутствие тока в цепи.
На этом математическом фундаменте Шеннон затем показал, что любой канал связи имеет свою максимальную пропускную способность для надежной передачи информации. В действительности он доказал, что, хотя можно приблизиться к этому максимуму за счет искусного кодирования, достичь его невозможно.







 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)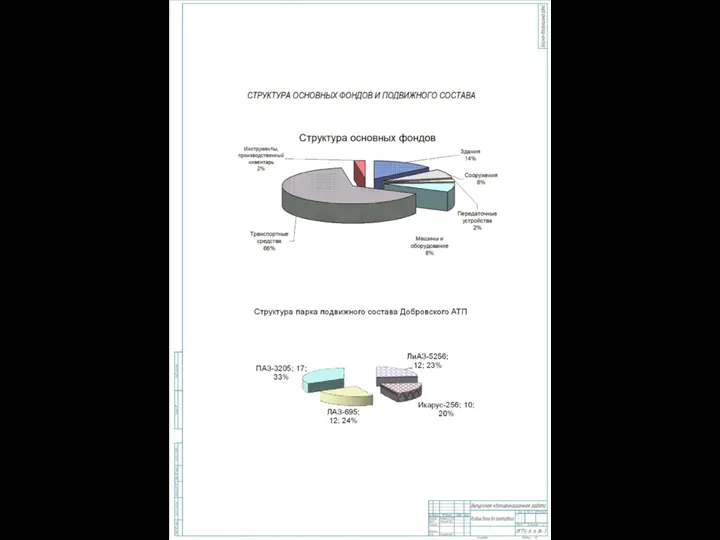 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС