Математические иллюзии

Давайте зададимся вопросом:,,Что такое обман зрения? Скорее всего ответите вы на этот вопрос так:обман зрения-это когда мы видим то,чего нет на самом деле ,и создает этот обман природа. Подтвердить это можно таким примером,как мираж в пустыне.Этот ответ верный,но не совсем полный.На самом деле не только природа создает обман зрения.Как известно,зрение даже самого здорового человека не идеально и именно наше с вами зрение зачастую создает обман.Доказать этот факт можно следующим примером.
Взгляните на представленную с боку картинку.Внимательно смотрите на точку(в середине картинки)и в этот момент двигайте головой назад и вперед.Вы увидите,что круги вращаются, это ОБМАН ЗРЕНИЯ.Вот на таком примере можно доказать,что иллюзии создает не только природа,но и человеческое зрение.
Иллюзии – это искаженное, неадекватное отражение свойств воспринимаемого объекта. В ПЕРЕВОДЕ С ЛАТЫНИ СЛОВО «ИЛЛЮЗИЯ» ОЗНАЧАЕТ «ОШИБКА, ЗАБЛУЖДЕНИЕ».

Некоторые ученики не понимают, зачем доказывать теоремы."Чего же тут рассуждать," – думают многие , начиная изучать геометрию. «Посмотришь на чертеж, и сразу видно, что доказывать ничего не надо, всё и так видно. Глаз не обманет».
Иллюзия Мюллера-Лайера

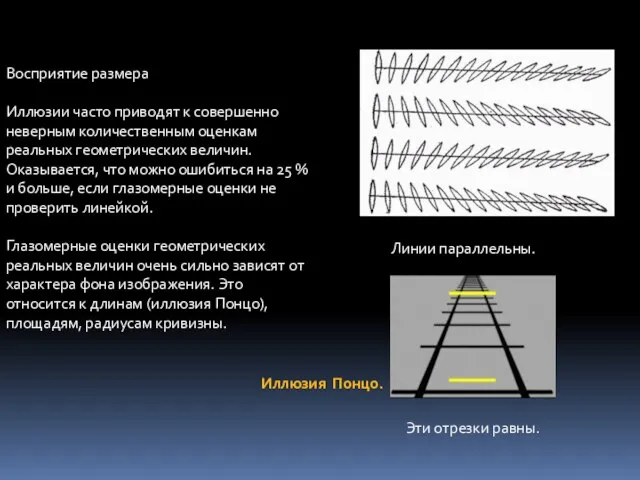
Восприятие размера
Иллюзии часто приводят к совершенно неверным количественным оценкам реальных геометрических величин. Оказывается, что можно ошибиться на 25 % и больше, если глазомерные оценки не проверить линейкой.
Глазомерные оценки геометрических реальных величин очень сильно зависят от характера фона изображения. Это относится к длинам (иллюзия Понцо), площадям, радиусам кривизны.
Эти отрезки равны.
Линии параллельны.
Иллюзия Понцо.

Геометрия изучает форму и взаимное расположение фигур (в пространстве – стереометрия, на плоскости – планиметрия).
С давних пор люди пытались объемные тела изобразить на плоскости так, чтобы их сразу можно было отличить от плоских, чтобы чувствовалась глубина пространства. Была разработана научная теория перспективы, позволяющая «обмануть» зрение.

Картинка венгерского художника ВИКТОРА ВАЗАРЕЛИ «ИЗУЧЕНИЕ ПЕРСПЕКТИВЫ» - прекрасный тому пример. Линии, уходящие вглубь, сходятся в одной точке, а фигура, находящаяся дальше от нас, изображается в виде формы меньших размеров.
Иллюзии рассматривают не только геометры, ими занимаются и физики, и психологи, и художники.

Иллюзия У. Эренштейна (W. Ehrenstein, 1921)
Примеры иллюзий.
Квадрат только кажется искаженным

Не отрывая взгляда от центра круга, подвигайте головой.
Возникла иллюзия, что узор вокруг шара сдвигается?

Смотрите в центр и двигайте головой вперед-назад.
В данном случае, иллюзия сильнее - она может возникать, даже если головой и не двигать.

Видите волны? Это не анимация, а статическая картинка!

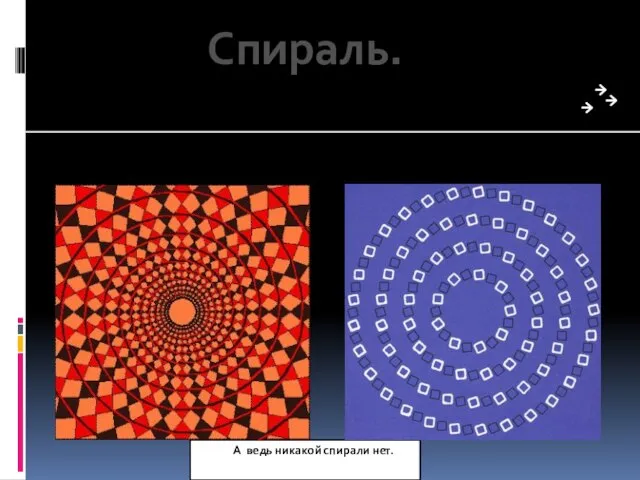
А ведь никакой спирали нет.
Спираль.

А ведь фигуры не двигаются.
.
Движущиеся фигуры

Спираль с оттенком голубого.
Если приблизится к экрану то увидите что голубого ничего нет, а есть оттенок зеленого.

Невозможное возможно.
В далеком 1934 году шведский художник ОСКАР РЕУТЕРСВАРД изобразил на одном из своих полотен треугольник, составленный из девяти абсолютно одинаковых кубиков. При более внимательном рассмотрении можно заметить противоречия в соединениях элементов фигуры,
словно кто-то отменил для нее законы физики!
Именно поэтому сей необычный объект и был назван
«невозможным треугольником» или «ТРИБАРОМ».

Однако по-настоящему знаменитой странная фигура стала в 1954 году, когда ее снова, притом совершенно независимо от Реутерсварда открыл английский физик и математик РОДЖЕР ПЕНРОУЗ. Он изобразил треугольник в его более привычном, «геометрическом» виде, но от этого фигура стала выглядеть еще более гротескной:
Интересно, что если прикрыть ладонью хоть один из углов «бешеного» треугольника, то наваждение сразу же пропадает. Можете проверить!

Художники используют эту фигуру в своих произведениях. Например, в церкви святой Троицы в Баррингтоне (Великобритания, Девон) можно встретить трибар:

ШАХМАТНАЯ ДОСКА.

Обман зрения в искусстве

Вывод: не всегда верьте своему зрению. Нужны математические расчеты измерения и доказательства,чтобы подтвердить истину.