Содержание
- 2. Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс Это математический объект, а не физическая машина Предложена
- 3. 1) Внешний алфавит А = {a0, a1, …, an} Элемент a0 называется пустой символ В этом
- 4. 2) Внутренний алфавит Q = {q0, q1, …, qm}, {П, Л, С} В любой момент времени
- 5. 3) Внешняя память (лента) Машина имеет ленту, разбитую на ячейки, в каждую из которых может быть
- 6. 3) Внешняя память (лента) Устройство машины Тьюринга Пустая клетка содержит a0. В каждый момент времени на
- 7. 4) Каретка (управляющая головка) Каретка машины располагается над некоторой ячейкой ленты – воспринимает символ, записанный в
- 8. 5) Функциональная схема (программа) Программа машины состоит из команд: Устройство машины Тьюринга Для каждой пары (qi,
- 9. Замечание 1) В недетерминированной машине может появиться несколько параллельных вычислительных процессов 2) Разные машины Тьюринга отличаются
- 10. К началу работы машины на ленту подается исходный набор данных в виде слова α Описание работы
- 11. Описание работы машины Тьюринга Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении,
- 12. Находясь в не заключительном состоянии, машина совершает шаг, который определяется текущим состоянием qi и обозреваемым символом
- 13. Описание работы машины Тьюринга В соответствии с командой qiaj → qkal Х выполняются следующие действия: 1)
- 14. При переходе машины в заключительное состояние q0 ее работа прекращается На ленте записан результат работы алгоритма
- 15. Машинным словом (конфигурацией) машины Тьюринга называется слово вида α1qkal α2, где α1 и α2 - слова
- 16. Конфигурация α1qkal α2 интерпретируется следующим образом: - машина находится в состоянии qk - каретка обозревает на
- 17. Пример Дана машина Тьюринга с внешним алфавитом А = {a0, 1, * }, алфавитом внутренних состояний
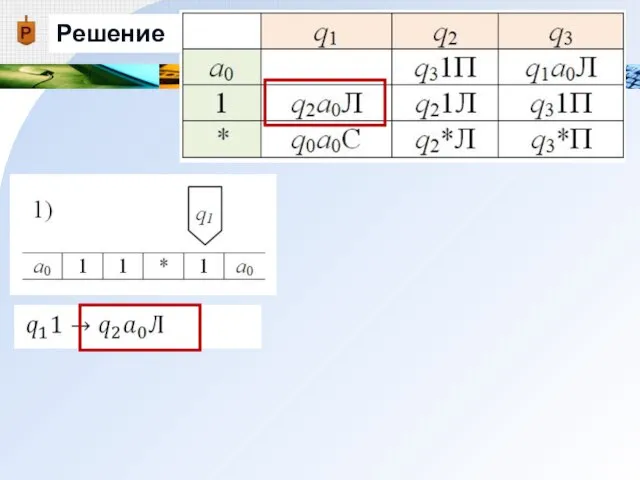
- 18. Решение
- 19. Решение 1) Заменяем содержимое обозреваемой ячейки 1 на а0
- 20. Решение 2) Машина переходит в новое состояние q2
- 21. Решение 3) Каретка перемещается влево
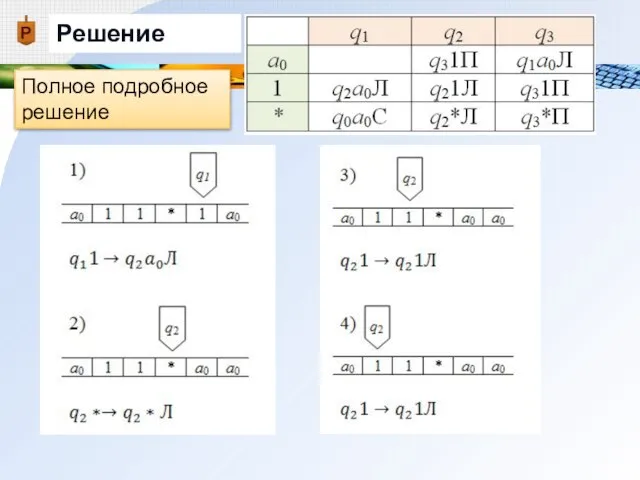
- 22. Решение Полное подробное решение
- 23. Решение Полное подробное решение
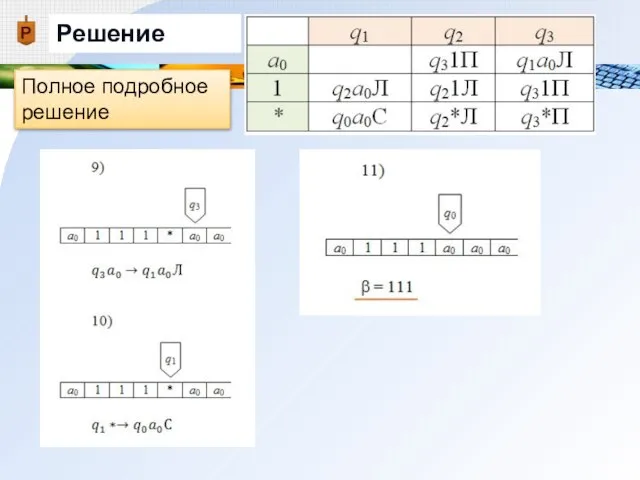
- 24. Решение Полное подробное решение
- 25. Решение Решение, записанное с помощью конфигураций (в строчку)
- 26. α = 1*11 Ответ: β = 111
- 27. Литература Игошин В.И. Математическая логика и теория алгоритмов. – М.: Академия, 2008. - 448 с. Лихтарников
- 29. Скачать презентацию























 Архитектура и живопись русского классицизма
Архитектура и живопись русского классицизма О ВЛИЯНИИ ЭКСПЕРИМЕНТАЛЬНЫХ УСТРОЙСТВ НА ФИЗИКУ И БЕЗОПАСНОСТЬ ИССЛЕДОВАТЕЛЬСКИХ РЕАКТОРОВ XIII ЕЖЕГОДНОЕ РОССИЙСКОЕ СОВЕЩАНИЕ «
О ВЛИЯНИИ ЭКСПЕРИМЕНТАЛЬНЫХ УСТРОЙСТВ НА ФИЗИКУ И БЕЗОПАСНОСТЬ ИССЛЕДОВАТЕЛЬСКИХ РЕАКТОРОВ XIII ЕЖЕГОДНОЕ РОССИЙСКОЕ СОВЕЩАНИЕ « Нанотехнологии - инвестиционный ресурс развития Удмуртской Республики
Нанотехнологии - инвестиционный ресурс развития Удмуртской Республики Правила санитарии, гигиены и безопасной работы
Правила санитарии, гигиены и безопасной работы Система аварийного ввода бора (СБВБ) на АЭС
Система аварийного ввода бора (СБВБ) на АЭС История эволюционных идей. Карл Линней
История эволюционных идей. Карл Линней Формирование исполнительского мастерства в условиях образовательной среды в ДШИ
Формирование исполнительского мастерства в условиях образовательной среды в ДШИ Документация как информационное обеспечение бухгалтерского учета
Документация как информационное обеспечение бухгалтерского учета Современная научная космология.
Современная научная космология. Расписание дня школьника
Расписание дня школьника Перспективы развития мультимодальных грузовых перевозок в Ульяновской области
Перспективы развития мультимодальных грузовых перевозок в Ульяновской области Почему невозможно утонуть в грязевом вулкане?
Почему невозможно утонуть в грязевом вулкане? Лекция 3Показатели энергосбережения и повышения энергетической эффективности
Лекция 3Показатели энергосбережения и повышения энергетической эффективности Образец бренда
Образец бренда Летняя оздоровительная кампания 2010год
Летняя оздоровительная кампания 2010год Компания Xerographic Print Service основана в 1994 г.в Нидерландах. Производственные филиалы работают в странах ЕС и Китае.
Компания Xerographic Print Service основана в 1994 г.в Нидерландах. Производственные филиалы работают в странах ЕС и Китае. Функциональное зонирование участка
Функциональное зонирование участка Һөйләмдең баш һәм эйәрсән киҫәктәре
Һөйләмдең баш һәм эйәрсән киҫәктәре Презентация на тему Поздравление с Новым годом
Презентация на тему Поздравление с Новым годом УМК для начальной школы
УМК для начальной школы Методическое объединение педагогов дополнительного образования и учителей художественно-эстетического цикла
Методическое объединение педагогов дополнительного образования и учителей художественно-эстетического цикла ЭКОЛОГ - Профессия XXI века?
ЭКОЛОГ - Профессия XXI века? Система контроля безопасности СКБ Dog
Система контроля безопасности СКБ Dog Детальный Углеводородный Анализ продуктов первичной переработки нефти, продуктов риформинга, готовой продукции
Детальный Углеводородный Анализ продуктов первичной переработки нефти, продуктов риформинга, готовой продукции Рекреационные ресурсы Луганщины
Рекреационные ресурсы Луганщины Filippovich_i_Bashkatova_1
Filippovich_i_Bashkatova_1 12 Декабря - День Конституции Российской Федерации
12 Декабря - День Конституции Российской Федерации Естественнонаучный турнир
Естественнонаучный турнир