Слайд 2Цель: изучить свойства топологии на примере листа Мебиуса.
Предмет: превращение листа Мебиуса в

зависимости от поставленных экспериментов.
Объект: лист Мёбиуса.
Гипотеза: если изучить поверхность листа Мебиуса, то можно сформулировать необычные свойства в геометрии Евклида.
Слайд 3Задачи
- спланировать работу в библиотеке;
- провести количественный и
качественный

анализ отобранного
материала;
- провести опыты по разрезанию листа
Мебиуса и эксперименты по
перекручиванию колец;
- обобщить полученные данные;
- приобрести навыки бумажного
моделирования и конструирования;
- изучить применения листа Мебиуса.
Слайд 4Методы
- поиск;
- отбор и анализ научной литературы;
- обобщение;
-

представление результатов;
- моделирование;
- конструирование.
Слайд 5Открытие листа Мебиуса.
А.Ф.Мебиус
И.Б.Листинг

Слайд 6Что же поразило этих двух немецких математиков?

Слайд 7А то что у листа Мебиуса одна сторона.

Слайд 10Опыт 1
Склеим полоску, получим обычное кольцо с двумя сторонами. Теперь разрежем это

кольцо вдоль посередине и получим два одинаковых кольца.
Слайд 11Изготовление модели
Возьмём бумажную полоску в форме прямоугольника ABCD (рис. 1)

Слайд 12Изготовление модели
Если перед склеиванием противоположных сторон одну из них повернуть на 180

градусов и соединить точку А с точкой С, а точку В с точкой D (рис. 2).
Слайд 14Опыт 2
Разрежем лист Мебиуса вдоль посередине и получим кольцо, перекрученное дважды, его
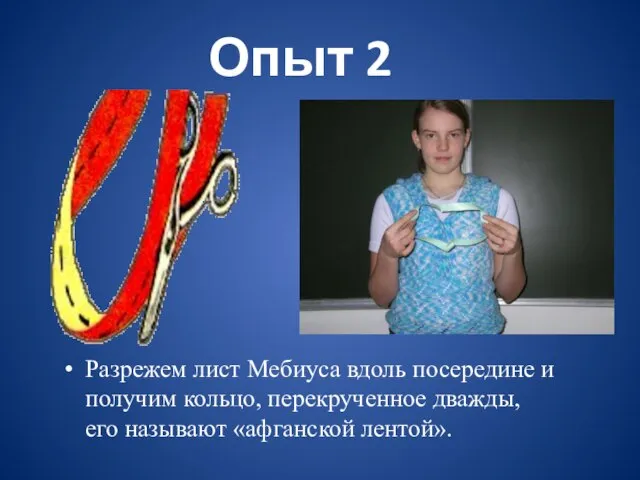
называют «афганской лентой».
Слайд 15Опыт 3
Если теперь «афганскую ленту» разрезать вдоль посередине, то получим две афганские

ленты, соединенные друг с другом.
Слайд 16Опыт 4
Если лист Мебиуса разрезать вдоль, отступив треть от края, мы получим

лист Мебиуса и «афганскую ленту» соединенные между собой.
Слайд 18Лист Мебиуса обладает любопытными свойствами:
- Имеет одну границу
- Неориентируемый
- Непрерывный
- Двусвязный
- Хроматический

номер – 6
Слайд 19Применения листа Мебиуса
Существуют технические применения ленты Мебиуса:
- В системах записи на непрерывную

пленку применялись ленты Мебиуса (чтобы удвоить время записи).
- В матричных принтерах красящая лента так же имеет вид листа Мебиуса для увеличения ее ресурса.
- Устройство под названием резистор Мебиуса – это недавно изобретенный электронный элемент, который не имеет собственной индуктивности.
Слайд 20Применение листа Мебиуса
Резистор
Наконечник бура

Слайд 21Предмет вдохновения
Лист Мебиуса является предметом вдохновения людей, работающих в различных областях искусства:
-

Лист Мебиуса постоянно встречается в научной фантастике, например в рассказе Артура Кларка «Стена Темноты».
- В произведениях уральского писателя Владислава Крапивина упоминается постоянно кольцо Мебиуса, цикл «В глубине Великого Кристалла» (например «Застава на Якорном поле. Поветь»)
Слайд 22Предмет вдохновения
- В рассказе А. Дж. Дейча «Лист Мебиуса» бостонское метро строит

новую линию, маршрут которой становится на столько запутанным, что превращается в ленту Мебиуса, после чего начинают исчезать поезда.
- На значке механико-математического факультета Московского университета изображен лист Мебиуса
Слайд 23Предмет вдохновения
Морис Корнелиус Эшер был одним из художников, кто особенно любил его

и посвятил несколько своих литографий этому математическому объекту. Одна из известных – лист Мебиуса II, показывает муравьев, ползающих по поверхности ленты Мебиуса.
























 Сопротивление человека
Сопротивление человека Формы проявления психических процессов и их взаимосвязь
Формы проявления психических процессов и их взаимосвязь Студенческий Event. Понятие бренда
Студенческий Event. Понятие бренда Презентация на тему Влияние на жизнь и здоровье людей природных катастроф
Презентация на тему Влияние на жизнь и здоровье людей природных катастроф Adidas performance outdoor ss'22
Adidas performance outdoor ss'22 Incubation. Illumination
Incubation. Illumination Инфографика
Инфографика Теория государства и права. Происхождение государства
Теория государства и права. Происхождение государства ФасадДомСтрой
ФасадДомСтрой Правовое регулирование реализации товаров, работ, услуг. Тема 6
Правовое регулирование реализации товаров, работ, услуг. Тема 6 Живая память
Живая память Критическое состояние окружающей природной среды в России
Критическое состояние окружающей природной среды в России Долина гейзеров на полуострове Камчатка
Долина гейзеров на полуострове Камчатка United Kingdom Political System
United Kingdom Political System Высшее образования 2010 год. Проблемы, задачи, перспективы развития
Высшее образования 2010 год. Проблемы, задачи, перспективы развития Наследственное право РФ
Наследственное право РФ Презентация на тему Древний Восток и античный мир 10 класс
Презентация на тему Древний Восток и античный мир 10 класс Источники и институты классического средневекового права
Источники и институты классического средневекового права Изучение органов кровообращения человека
Изучение органов кровообращения человека Задачи по теме
Задачи по теме Вагинальные инфекции
Вагинальные инфекции бенчмарки_карточка_товара_акции
бенчмарки_карточка_товара_акции 1
1 불규칙 동사
불규칙 동사 Transformatori
Transformatori Ama Kids, рейтинг
Ama Kids, рейтинг Вирусы гриппа
Вирусы гриппа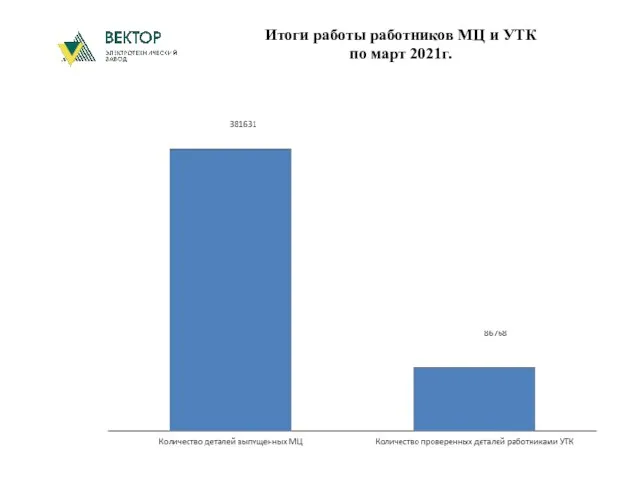 Электротехнический завод Вектор. Итоги работы работников МЦ и УТК
Электротехнический завод Вектор. Итоги работы работников МЦ и УТК