Математические основы компьютерной графики

Компьютерная графика – это к настоящему времени достаточно развитая и многосторонняя отрасль знания. Существует аппаратное и программное обеспечение для получения разнообразных изображений – от простых иллюстраций и чертежей до реалистических образов естественных объектов. Спектр использования компьютерной графики чрезвычайно широк: реклама и различного рода презентации, компьютерные игры и мультипликация, малые и монументальные формы дизайна, компьютерная живопись и архитектура, медицина, проектно-конструкторские разработки, административное управление и т.д. и т.п. Особое значение приобретает компьютерная графика в науке и образовании, становясь фактически новым инструментарием в процессе получения знаний.

История
Первые вычислительные машины не имели отдельных средств для работы с графикой, однако уже использовались для получения и обработки изображений. Программируя память первых электронных машин, построенную на основе матрицы ламп, можно было получать узоры.
В 1961 году программист С. Рассел возглавил проект по созданию первой компьютерной игры с графикой. Создание игры «Spacewar» («Космические войны») заняло около 200 человеко-часов. Игра была создана на машине PDP-1.
В 1963 году американский учёный Айвен Сазерленд создал программно-аппаратный комплекс Sketchpad, который позволял рисовать точки, линии и окружности на трубке цифровым пером. Поддерживались базовые действия с примитивами: перемещение, копирование и др. По сути, это был первый векторный редактор, реализованный на компьютере. Также программу можно назвать первым графическим интерфейсом, причём она являлась таковой ещё до появления самого термина.
В середине 1960-х гг. появились разработки в промышленных приложениях компьютерной графики. Так, под руководством Т. Мофетта и Н. Тейлора фирма Itek разработала цифровую электронную чертёжную машину. В 1964 году General Motors представила систему автоматизированного проектирования DAC-1, разработанную совместно с IBM.
В 1968 году группой под руководством Константинова Н.Н. была создана компьютерная математическая модель движения кошки. Машина БЭСМ-4, выполняя написанную программу решения дифференциальных уравнений, рисовала мультфильм «Кошечка», который для своего времени являлся прорывом. Для визуализации использовался алфавитно-цифровой принтер.
Фундаментом для формирования и редактирования изображений служат математические и алгоритмические основы компьютерной графики (в первую очередь, это относится к изображениям, закодированным в векторной форме). Изучению именно таких основ компьютерной графики, используемых при обработке графических данных для вывода изображения на растровое графовыводящее устройство, а также последующего его видоизменения.

Математические основы компьютерной графики :
Преобразования в двухмерном пространстве
Преобразования в трехмерном пространстве
Аффинное проецирование
Перспективное проецирование
Стереографическая и специальные перспективные проекции
Масштабирование в окне
Нахождение параметров плоскости

Преобразования в двухмерном пространстве
Преобразования в двухмерном пространстве используются в разнообразных случаях: чтобы отдельные части объекта можно было описывать в различных координатных системах; чтобы типовые и повторяющиеся части можно было располагать в произвольных положениях на чертеже и в пространстве, в том числе с использованием циклов; чтобы без повторной кодировки можно было получать симметричные части объекта; для направленной деформации фигур, тел и их частей; для изменения масштаба чертежа, построения проекций пространственных образов... С аналитической точки зрения преобразования — это пересчет значений координат.
Преобразование точки
Точка на плоскости представляется двумя координатами: |x y|. Матрица преобразования точки выглядит так:
Ниже показано преобразование точки через квадратную матрицу; здесь xn = xa + yc и yn = xb + yd — новые координаты точки после преобразования:
Преобразование фигуры
Если представить фигуру как совокупность точек, то можно провести и ее преобразование. В следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1), каждая из которых после преобразования переходит соответственно в A*(0, 0), B*(a, b), C*(a + c, b + d), D*(c, d):
Геометрически это соответствует деформации фигуры:
При этом площадь новой фигуры равна площади старой фигуры, умноженной на детерминант матрицы преобразования: S2 = S1 * |ad - bc|.

Однородные координаты. Операции в них
Любая система координат, в которой представление точки в двухмерном (трехмерном) пространстве задается при помощи трех (четырех) координат (Р1, Р2, Р3(, Р4)), называется системой однородных координат. Вообще, для n-мерного пространства число однородных координат должно быть на единицу больше: n + 1.
Применение однородных координат в общем случае позволяет устранять аномалии, возникающие при работе в декартовых координатах, и представлять сложные преобразования в виде произведения нескольких матриц.
Геометрическая интерпретация на случай двухмерного пространства: введение третьей координаты, равной единице, можно трактовать как переход в трехмерное пространство, в котором разрешено работать только в плоскости z = 1. Следует представлять себе, что экран компьютера (картинная плоскость, плоскость изображения) находится в плоскости z = 1:
В случае выхода рисунка за сечение z = 1 рисунок возвращается принудительно в данное сечение — для того, чтобы были возможны последующие операции:
Такая операция называется нормализацией однородных координат:
Общий вид преобразования
Операция смещения
Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц — вдоль оси y:

Операция масштабирования
За счет коэффициентов a и d матрицы преобразования происходит
увеличение (или уменьшение) значения координат точки (x, y) в a и
d раз по осям x и y соответственно:
Общее полное масштабирование
В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект — уменьшение значения координат (x, y) в s раз.
Поворот на угол q
Здесь q — угол, на который требуется повернуть точку (x, y). Обратите внимание: поворот происходит относительно точки (0, 0) декартовой системы координат против часовой стрелки!
Отображение или зеркалирование
Зеркалирование относительно прямой y = x (рис. 1.6a):
Зеркалирование относительно прямой x = 0 (рис. 1.6b):
Зеркалирование относительно прямой y = 0 (рис. 1.6c):
Зеркалирование относительно начала координат (рис. 1.6d):

Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a
Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол a; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.
Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x1, y1), C(x2, y2) вокруг точки D(m, n) на угол a. Пусть P-s — матрица переноса точки на вектор A(-m, -n), Va — матрица поворота на угол a, Ps — матрица переноса точки на вектор A'(m, n).
Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки A(x, y):
Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.
Центральное проецирование (перспектива)
px + qy + 1 = H — плоскость.

Преобразования в трехмерном пространстве
На прошлой лекции мы изучили операции, которые можно выполнять с точкой на плоскости. Такие же операции имеются и в трехмерном пространстве. Отличие здесь небольшое: точка задается не двумя, а тремя координатими, и при работе в однородных координатах матрицы преобразований/операций будут состоять не из трех, а из четырех столбцов.
Операция смещения
Операция масштабирования
Общее полное масштабирование
Матрицы поворота вокруг осей x, y, z на угол a
Rx Ry Rz

Поворот тела вокруг точки (m, n, k) на угол a
Разобъем данную операцию на базовые (простейшие), а именно: 1) перенос тела на вектор A(-m, -n, -k) для совмещения точки (m, n, k) с началом координат; 2) поворот тела на угол a; 3) перенос тела на вектор A'(m, n, k) для возвращения его в исходное положение. Представим тело набором точек (вершин тела) и выполним операции 1) - 3) с каждой из них; в матричной форме это представляется следующим образом (R(a) — матрица поворота вокруг оси x, y или z):
Зеркалирование
Замечание: ниже представлены всего лишь три матрицы зеркалирования, на самом деле их больше. Предлагаем читателю самостоятельно построить недостающие матрицы.
Зеркалирование относительно оси z:
Зеркалирование относительно плоскости x = 0:
Зеркалирование относительно начала координат:
Вращение тела на угол q вокруг произвольной оси, проходящей через точку (0, 0, 0)
Здесь a — угол наклона относительно оси x, b — угол наклона относительно оси y, g — угол наклона относительно оси z.

Аффинное проецирование
Геометрия аффинная
Аксонометрическая (прямоугольная) проекция
Ортографическая проекция
Ортогональная проекция
Диметрическая проекция
Изометрическая проекция
Косоугольная проекция
Проекция Кабине
Проекция Кавалье
Геометрия перспективная
Перспективная проекция
Одноточечная проекция
Двухточечная проекция
Трехточечная проекция
Аффинная геометрия является чертежным средством; в этой геометрии используется параллельное проецирование, которое осуществляется пучком параллельных прямых (см. рис. 3.1, слева). Детерминант матрицы преобразований в аффинной геометрии равен нулю. Геометрия перспективная является художественным средством, в ней отсутствуют параллельные линии и используется центральное проецирование, при котором все линии сходятся у горизонта в одну точку (см. рис. 3.1, справа); за счет того, что одна, две или три компоненты четвертого столбца матрицы преобразований не равны нулю, ее детерминант также не равен нулю.
Наиболее распространены аффинные двухмерные и трехмерные преобразования. Их основные геометрические свойства: прямые линии после преобразования остаются прямыми, параллельные — параллельными, плоскости остаются плоскостями и параллельные плоскости — параллельными. Вычерчивание трехмерных объектов, независимо от того на бумаге ли это происходит или на экране дисплея, осуществляется при помощи двухмерных проекций. В плоской проекции каждая точка предмета проецируется определенным образом на плоскость проекции, и ее образ называется точкой проекции. Если линии проекции, соединяющие точки предмета с соответствующими точками проекции, параллельны, то мы имеем плоскую параллельную проекцию. Если же линии проекции сходятся в одной общей точке, то получаемое изображение называется центральной проекцией, или перспективным изображением предмета.
Рассмотрим далее несколько видов аксонометрических проекций. Заметим, что среди них выделяются прямоугольные (ортогональные) проекции — те, у которых проецирующие лучи перпендикулярны к плоскости изображения. Слова «аксонометрическая» и «прямоугольная» часто используют как синонимы.

Аксонометрическая ортографическая проекция
Смещает изображение по оси z на n единиц и проецирование
происходит в плоскости z = 0:
Аксонометрическая ортогональнальная проекция
Проецирующие лучи перпендикулярны к плоскости изображения, и плоскость проекции совпадает с одной из координатных плоскостей.
Пример: выполним поворот куба (рис. 3.2, слева) относительно оси x на угол 90o и спроецируем его на плоскость z = 0 (рис. 3.2, справа). Обратите внимание, что точки, которые после поворота на куба на 90o будут лежать на проецирующих лучах (пары A и C, B и D и т. д.), после преобразования займут одинаковое положение (пары Aн и Cн, Bн и Dн и т. д.):
Запись в матричной форме:
Аксонометрическая диметрическая проекция
В этом случае были специально подобраны коэффициенты,
дающие минимальные искажения какого-либо изображения:
Аксонометрическая изометрическая проекция
В общем смысле дает проекцию с изменением масштаба:
Надо заметить, что любая проекция имеет свои достоинства и недостатки (искажение размеров изображения по одной из осей, неодинаковость сокращения размеров по разным осям, заслонения точек друг другом), поэтому каждая из них используется там, где это более удобно: ортографическая — только для переноса и проецирования, ортогональная — для вращения и проецирования; при диметрической проекции изображение по оси y имеет натуральный размер, а по осям x и z оно одинаково сокращено (то есть на экране размер линии по x и по y уменьшен в А раз по отношению к натуральному размеру на объекте); при изометрической проекции изображение по трем осям одинаково сокращено.

Перспективное проецирование
На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Эти изображения называют перспективными. Свойства их таковы, что более удаленные предметы изображаются в меньших масштабах, параллельные прямые в общем случае непараллельны. В итоге геометрия изображения оказывается достаточно сложной, и по готовому изображению сложно определить размер тех или иных частей объекта.
Обычная перспективная проекция — это центральная проекция на плоскость прямыми лучами, проходящими через точку — центр проецирования. Один из проецирующих лучей перпендикулярен к плоскости проецирования и называется главным. Точка пересечения этого луча и плоскости проекции — главная точка картины.
Существует три системы координат. Обычно программист работает и держит данные о геометрических объектах в мировых координатах. Для повышения реалистичности при подготовке к выводу изображения на экран данные об объектах из мировых координат переводят в видовые координаты. И только в момент вывода изображения непосредственно на экран дисплея переходят к экранным координатам, которые представляют собой номера пикселов экрана.
Первые две системы могут использоваться в многомерных системах координат, но последняя только в двухмерной. Операции являются необратимыми, то есть из двухмерной картинки-проекции невозможно восстановить трехмерное изображение.
Матрица общего перспективного преобразования
В этой матрице элементы a, d, е отвечают за масштабирование, m, n, L — за смещение, p, q, r — за проецирование, s — за комплексное масштабирование, х — за вращение.
Одноточечное проецирование на плоскость z = 0
Суть этого проецирования такова: чем глубже находится предмет, тем больше становится значение z-координаты и знаменателя rz + 1, и, следовательно, тем мельче выглядит предмет на плоскости проекции. Выполним несложные выкладки и поясним их графически:

уравнение x'/F = x/(F + zпр) равносильно: x' = xF/(F + zпр) = x/(1 + zпр/F) = x/(1 + rzпр), где r = 1/F, F — фокус.
Для того, чтобы точки, лежащие на линии, параллельной оси z, не терялись друг за другом, используется одноточечное проецирование на линию (см. матрицу преобразования и рис. 4.2); исчезла z-координата, но, поскольку дальние предметы стали более мелкими, чем такие же близкие, у зрителя появляется ощущение глубины. Запомните: это первый способ передачи глубины на плоскости!
А теперь для примера отобразим куб, стороны которого равны
единице (см. рис. 4.3), на плоскость z = 0; пусть на оси z фокус F = -10 и,
следовательно, r = -1/10 = -0.1:

В плоскости экрана после преобразования мы будем иметь следующее изображение:
Обратите внимание: если бы центр тяжести куба
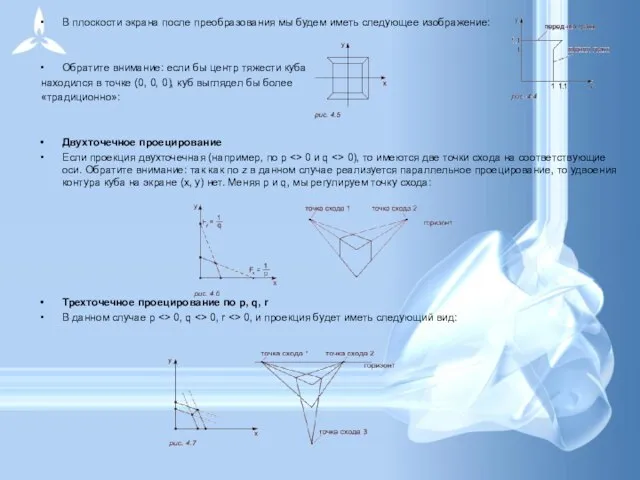
находился в точке (0, 0, 0), куб выглядел бы более
«традиционно»:
Двухточечное проецирование
Если проекция двухточечная (например, по p <> 0 и q <> 0), то имеются две точки схода на соответствующие оси. Обратите внимание: так как по z в данном случае реализуется параллельное проецирование, то удвоения контура куба на экране (x, y) нет. Меняя p и q, мы регулируем точку схода:
Трехточечное проецирование по p, q, r
В данном случае p <> 0, q <> 0, r <> 0, и проекция будет иметь следующий вид:

Стереографическая и специальные перспективные проекции
Чтобы помочь человеку осознать, что на экране перед ним — именно трехмерное изображение (то есть восстановить третью координату из двумерного изображения), используются различные приемы: нанесение штриховки, окраска, дымка, уменьшение размеров с глубиной, тени, стерео... Рассмотрим подробнее последний способ.
Разберемся, каким же образом мы определяем объем, глубину в изображении? Для этого надо понять, как и с помощью чего мы «чувствуем» третье измерение? Оказывается, человек чувствует глубину по напряжению аккомодационной мышцы глаза. Чем ближе к глазу находится объект, тем сильнее напрягается эта мышца и тем сильнее она выгибает глазной хрусталик. Таким образом, очень сильное напряжение аккомодационной мышцы сообщает мозгу о том, что предмет находится очень близко.
Так как глаза человека находятся на некотором расстоянии друг от друга, один и тот же предмет они видят немного по-разному. На рис. 5.1 точка x1 — это изображение предмета на плоскости проекции для правого глаза, x2 — для левого, F — расстояние от глаз до плоскости проекции (около 50 см.), d — расстояние между глазами (около 5 см.), a = arctg(d/F) — стереоугол (около 5.71o):
Таким образом, чтобы создать для глаз эффект стерео,
необходимо сформировать два изображения —
для левого и правого глаза. Ниже даны
соответствующие матрицы:
левый глаз правый глаз
Обратим внимание на некоторые элементы матриц. Значение -1/F говорит о том, что проецирование идет по оси z; третий столбец матриц состоит из одних нулей — это указывает на то, что проецирование идет на плоскость z = 0; F/20 = d/2 и -F/20 = -d/2 задают смещение по оси x для левого и правого глаза соответственно.
Существуют различные способы рассматривания полученных изображений. Первый способ применяется в виртуальных шлемах: изображение с помощью крохотных жидкокристаллических дисплеев подается отдельно на каждый глаз. Другой способ — анаглифический. В этом случае картинка для левого глаза окрашивается в синий цвет, а для правого — в красный; зритель надевает специальные фильтры-очки с синими и красными стеклами — и одним глазом видит только первое изображение, а другим — только второе. Мозг наблюдающего воспримет такую картину как единое объемное стереоизображение.

Специальная перспективная проекция на сферу («рыбий глаз»)
В отличие от классической перспективы, в перспективной проекции на сферу каждую часть изображения лучше рассматривать перпендикулярно к сфере, то есть при просмотре различных частей проекции голова наблюдающего или рисунок перемещаются. Такое рассматривание можно назвать фрагментарным.
za = zпр * F
C = 2F/[za + sqrt(x2пр + y2пр + z2a)]
x' = xпр * C
y' = yпр * C
Взгляните на рис. 5.2. Луч, выходящий из точки М, есть луч проецирования на сферу в точке P. Точка S является центром проекции. Луч, выходящий из точки S' и проходящий через P и М', — это луч перепроецирования со сферы на плоскость.
Специальная перспективная проекция на цилиндрическую поверхность
Проекция на цилиндрическую поверхность позволяет показывать объекты с очень большими углами зрения по горизонтали, вплоть до круговой панорамы. Вычерчиваются проекции в виде разверток на обычных графических устройствах.
z'пр = zпр + F
y'/y = (F + zпр)/F, y = y'F/(F + zпр) = y'F/z'пр
x' = F * arctg(xпр/za)
y' = F * y/sqrt(x2пр + z2пр)
На рис 5.3 S — центр проекции (точка зрения), z — главная ось.

Масштабирование в окне
Масштабирование
Для того, чтобы выполнить масштабирование, необходимо:
задать или определить координаты размера изображения: xmin, ymin, xmax, ymax и координаты области вывода: Xmin, Ymin, Xmax, Ymax;
вычислить коэффициенты масштабирования:
fx = (Xmax - Xmin) / (xmax - xmin),
fy = (Ymax - Ymin) / (ymax - ymin),
fx = fy = min(fx, fy)
произвести вычисление текущих координат экрана:
xэ = Xmin + fx * (xр - xmin),
yэ = Ymin + fy * (yр - ymin),
где xэ, yэ — экранные координаты, xр, yр — реальные координаты.

Нахождение параметров плоскости
Нахождение плоскости по точкам
Пусть уравнение ax + by + cz + d = 0 описывает плоскость. Переменная d является свободной, ей можно придать любое значение, положим ее равной единице: d = 1. Известно, что плоскость задается, причем однозначным образом, тремя точками (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) пространства (эти точки, вообще говоря, не должны одновременно находиться на одной прямой):
x1a + y1b + z1c = -1
x2a + y2b + z2c = -1
x3a + y3b + z3c = -1
Решив эту систему уравнений относительно неизвестных a, b и c, мы найдем уравнение плоскости. Покажем это на примере. Найдем уравнение плоскости, проходящей через три точки: A(1, 0, 0), B(0, 1, 0), C(1, -1, 1). Рис. 7.1 иллюстрирует нашу задачу:
Представим систему уравнений в виде произведения матриц: первая из них содержит координаты точек A, B и C, вторая — неизвестные a, b и c, третья — правые части уравнений:
Отсюда находим a = -1, b = -1, c = -1 и подставляем их в уравнение плоскости: -1x - 1y - 1z + d = 0 или x + y + z = d. Подставим в это уравнение плоскости любую точку, например, (1, 0, 0) и найдем d: d = 1. Окончательно уравнение данной плоскости выглядит так: x + y + z - 1 = 0.
Представим систему уравнений в виде произведения матриц: первая из них содержит координаты точек A, B и C, вторая — неизвестные a, b и c, третья — правые части уравнений:
Отсюда находим a = -1, b = -1, c = -1 и подставляем их в уравнение
плоскости: -1x - 1y - 1z + d = 0 или x + y + z = d. Подставим в это
уравнение плоскости любую точку, например, (1, 0, 0) и найдем d: d = 1. Окончательно уравнение данной плоскости выглядит так: x + y + z - 1 = 0.