Слайд 2
Сетевой график – информационно-динамическая модель, отражающая взаимосвязи между работами, необходимые для достижения

конечной цели проекта.
Слайд 3Работами являются любые действия, приводящие к достижению определенных результатов – событий.
События,

кроме исходного, являются результатами выполнения работ.
Между двумя смежными событиями может выполняться только одна работа или последовательность работ.
Слайд 4Путь – последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую

вершину.
Длина пути – суммарная продолжительность выполнения всех работ пути.
Полный путь – это путь от исходного к завершающему событию.
Критический путь – полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.
Слайд 52 подхода к построению сетевых моделей.
«Работа-стрелка», сетевые графики:
стрелками на графике изображаются
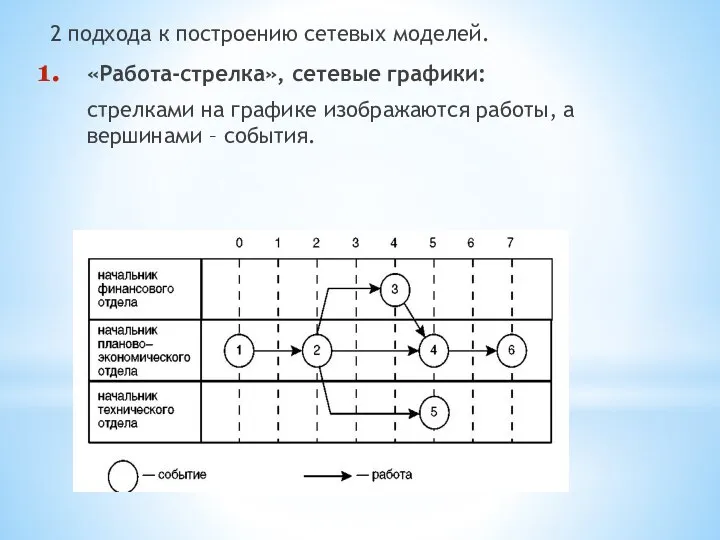
работы, а вершинами – события.
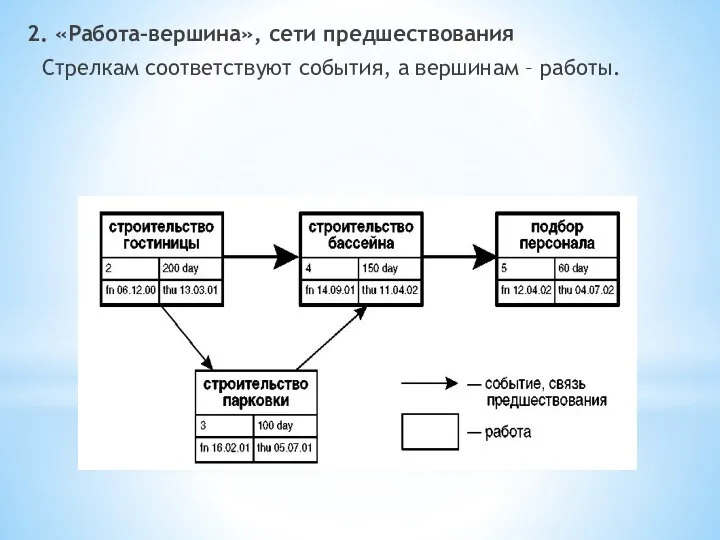
Слайд 62. «Работа–вершина», сети предшествования
Стрелкам соответствуют события, а вершинам – работы.
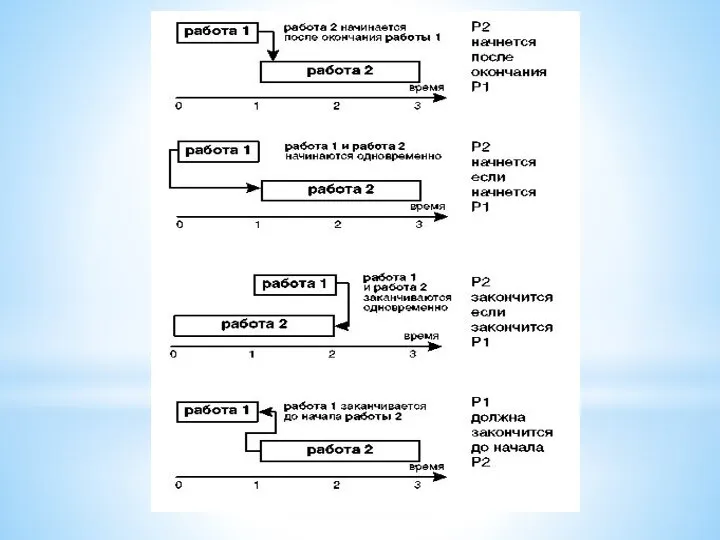
Слайд 7Для построения сетевых моделей необходимо определить логические взаимосвязи между работами.
Причиной взаимосвязей

являются, как правило, технологические ограничения (начало одних работ зависит от завершения других).
Комплекс взаимосвязей между работами определяет последовательность выполнения работ во времени.
Для определения последовательности действий необходима следующая информация: перечень работ, описание продукта, технологические, взаимосвязи, ограничения и предположения.
Слайд 10Разработка
идеального календарного графика работ
Цель: минимизация временных затрат на выполнение работ за

счет проведения оценки длительности выполнения по каждой из них.
При определении идеальных оценок длительности работ пренебрегают ограничениями ресурсов и учитывают только технологические ограничения и нормативы.
Результаты определения длительности работ вводят в сетевую модель и определяют общую продолжительность проекта.
Слайд 11Уменьшение общей длительности проекта возможно за счет:
сокращения времени выполнения отдельных работ

организации их параллельного выполнения
устранения временных разрывов.
Для выделения работ, определяющих минимальную длительность проекта, применяется метод критического пути.
Слайд 12Для временной оптимизации сетевой модели необходимо определить именно те работы, которые в
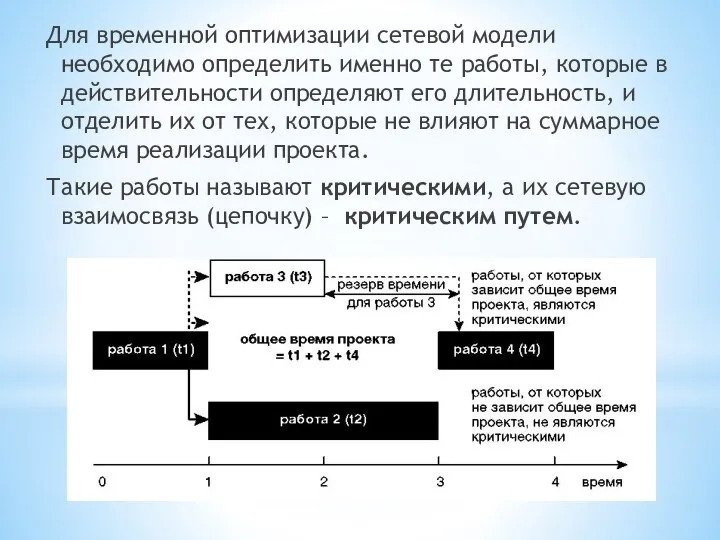
действительности определяют его длительность, и отделить их от тех, которые не влияют на суммарное время реализации проекта.
Такие работы называют критическими, а их сетевую взаимосвязь (цепочку) – критическим путем.
Слайд 13Методика определения критического пути
Критический путь – наиболее протяженная по времени цепочка работ,

ведущая от исходного к завершающему событию.
Изменение продолжительности любой работы, лежащей на критическом пути, соответственным образом меняет (сокращает или удлиняет) срок наступления завершающего события, т.е. дату завершения проекта, поскольку работы, лежащие на критическом пути не имеют резерва времени.
Все работы, которые лежат вне критического пути, имеют резерв времени, на которое может быть отсрочено наступление завершения данной работы без нарушения сроков проекта в целом.
Резерв времени работы определяется как разность между поздним и ранним сроками завершения работы.
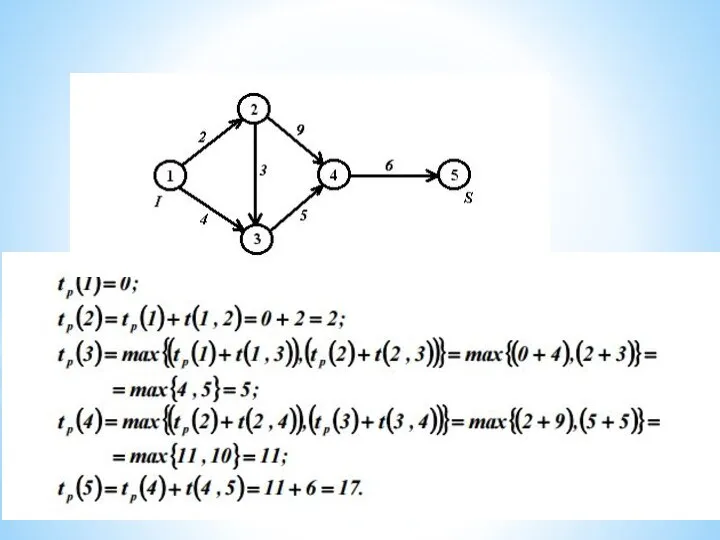
Ранний из возможных сроков наступления окончания работы – это срок, необходимый для выполнения всех работ, предшествующих данной. Поздний из допустимых сроков – это такой промежуток времени, на который может быть отсрочено наступление окончания данной работы без нарушения сроков проекта в целом.
Все работы лежащие вне некритического пути обладают резервами времени в рамках которых их можно сдвигать, не приводя к изменению времени выполнения всего проекта
Слайд 14Методика определения критического пути
Прямой проход начинается с начальной даты проекта и продолжается

по сетевому графику, при этом для каждой работы к начальному сроку прибавляется ее продолжительность и вычисляется раннее начало и раннее окончание этой работы. Самыми ранними возможными датами для работы являются ее начало и конец, допустимые исходя из логической последовательности сетевого графика.
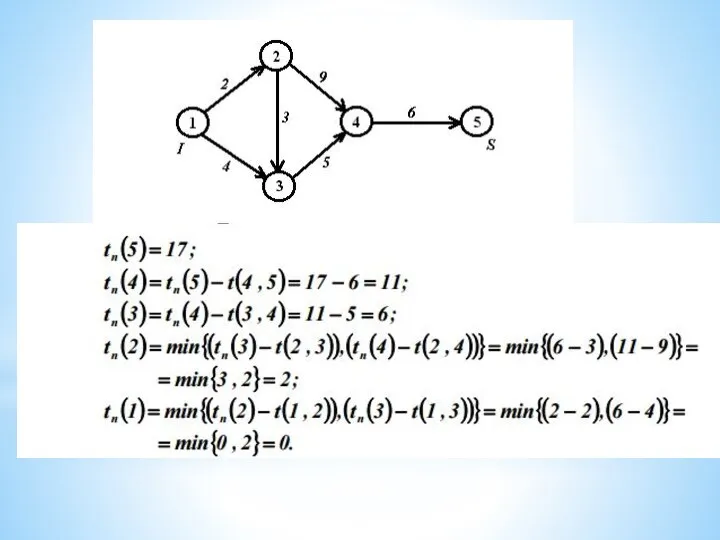
Обратный проход использует в качестве исходной точки конечную дату расписания, вычисленную путем прямого прохода, и проводится обратный расчет для определения поздних дат начала и окончания работ. Поздними датами работы являются ее самые поздние допустимые начало и конец, не влекущие задержки выполнения всего проекта.
Кроме того, на основании рассчитанных ранних и поздних дат начала работ определяются величины временных резервов для каждой работы.
Слайд 15Разработка реального календарного графика работ
Практический смысл этого шага проектирования состоит в том,

чтобы учесть все необходимые ресурсы, правильно оценить и распределить их.
Ресурсами, планируемыми в проекте, являются ресурсы материальные и человеческие. Все они имеют стоимостную оценку, однако ее недостаточно для планирования, важно оценить такие параметры как наличие ресурсов и их доступность, качество, сезонность и многое другое.
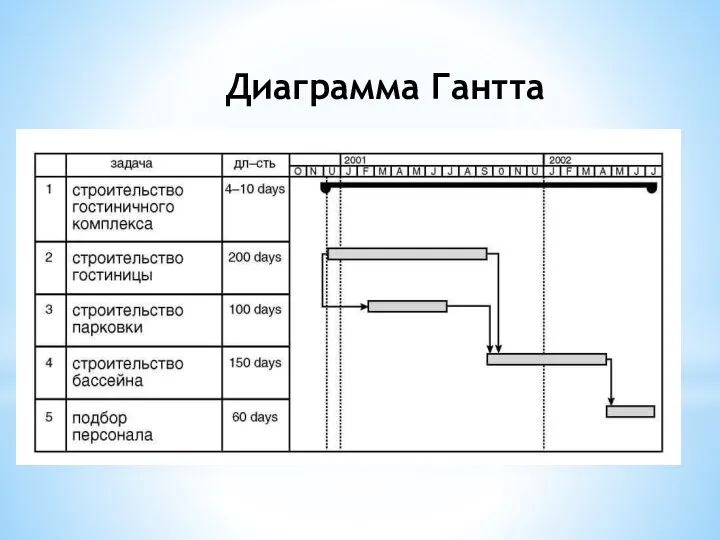
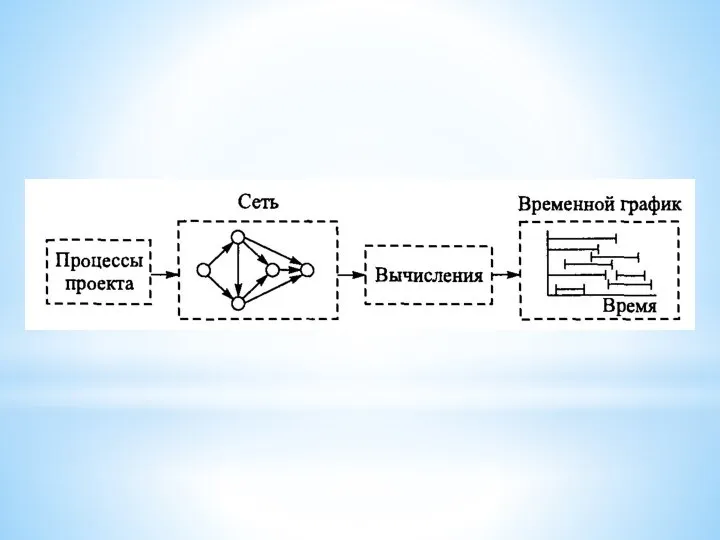
Слайд 17Этапы сетевого планирования:
Разбиение проекта на четко определенные работы, для которых определяется продолжительность.

Построение сетевого графика, показывающей последовательность работ, составляющих проект.
На третьем этапе на основе построенной сети выполняются вычисления, в результате которых составляется временной график реализации проекта
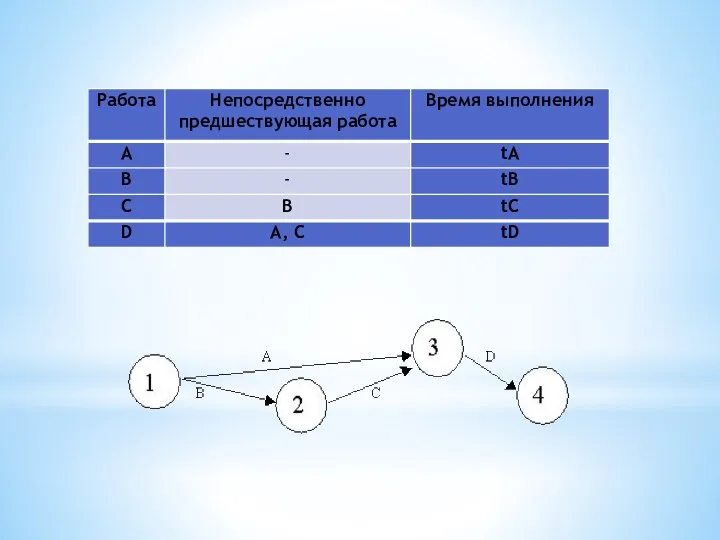
Слайд 19
Каждая вершина графа отображает событие (момент времени, когда завершаются одни работы и

начинаются другие).
Событие 1 означает начало выполнения проекта.
Событие 4 означает завершение проекта.
Любая работа проекта – это упорядоченная пара двух событий.
Например, работа A есть упорядоченная пара событий (1,3).
Работа D – упорядоченная пара событий (3,4).
Событие проекта состоит в том, что завершены все работы, «входящие» в соответствующую вершину. Например, событие 3 состоит в том, что завершены работы A и C.
Слайд 20Построение сети проекта основано
на следующих правилах:
1. Каждая работа в проекте представляется

одной и только одной дугой.
2. Каждая работа идентифицируется двумя концевыми узлами
3. Для поддержания правильных отношений предшествования при включении в сетевой график любой работы необходимо ответить на следующие вопросы.
Какая работа непосредственно предшествует текущей?
Какая работа должна выполняться после завершения текущей работы?
Какая работа конкурирует (выполняется параллельно) с текущей?
Слайд 21Ответы на эти вопросы, возможно, потребуют включить в сеть фиктивные работы, чтобы

правильно отобразить последовательность выполнения работ. Предположим, например, что четыре работы должны удовлетворять следующим условиям.
1. Работа С должна начаться сразу после завершения работ А и В.
2. Работа Е должна начаться непосредственно после завершения работы В.
Неправильное представление работ, так как из него следует, что работа Е должна начаться после завершения как работы В, так и А.
Решение проблемы с помощью фиктивной работы D:
Фиктивная работа может реально существовать, например, «передача документов от одного отдела к другому». Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0.
Слайд 22В сетевом графике не должно быть:
«висячих» событий (т.е. не имеющих предшествующих событий),

кроме исходного;
тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего;
циклов
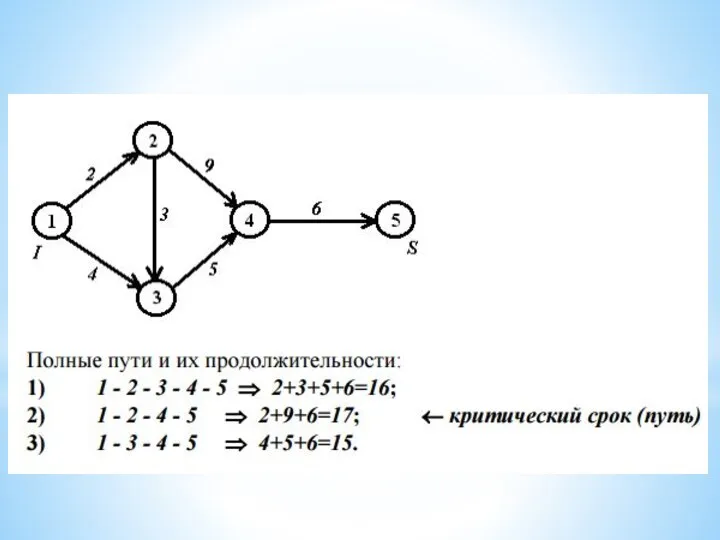
Слайд 23Определение критического пути.
Путь – последовательность взаимосвязанных работ, ведущая из одной вершины
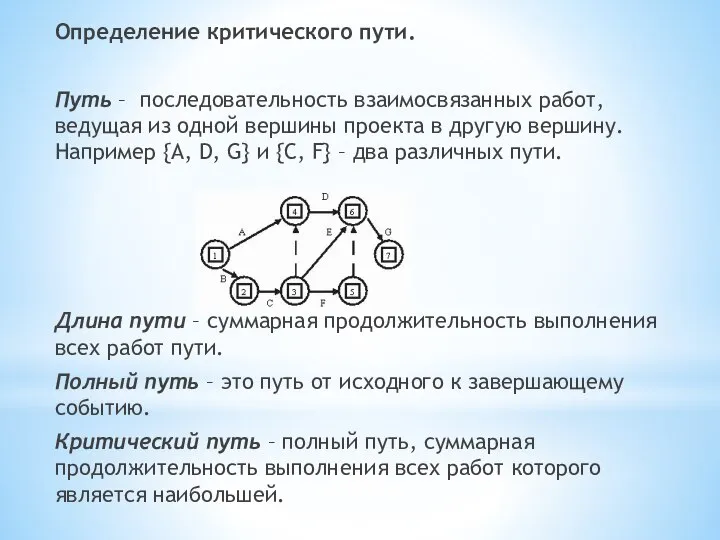
проекта в другую вершину. Например {A, D, G} и {C, F} – два различных пути.
Длина пути – суммарная продолжительность выполнения всех работ пути.
Полный путь – это путь от исходного к завершающему событию.
Критический путь – полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.




















 Презентация на тему Взаимодействие света с веществом Дисперсия света
Презентация на тему Взаимодействие света с веществом Дисперсия света
 Бизнес-план. Создание детского кафе Счастливое детство
Бизнес-план. Создание детского кафе Счастливое детство Современные и забытые виды спорта
Современные и забытые виды спорта СВЯЗЬ ИННОВАЦИИ СЕРВИС
СВЯЗЬ ИННОВАЦИИ СЕРВИС Аттестационная работа. Пищевые добавки и их влияние на организм
Аттестационная работа. Пищевые добавки и их влияние на организм ООО МДО Душанбе Сити
ООО МДО Душанбе Сити Понятие о профессии, специальности и квалификации работника. Классификация профессий
Понятие о профессии, специальности и квалификации работника. Классификация профессий Производственное здание и зем. участок
Производственное здание и зем. участок Эффекта не вмешивающегося свидетеля (синдром Дженовезе)
Эффекта не вмешивающегося свидетеля (синдром Дженовезе) Программа Intel «Путь к успеху» Итоги развития программы в 2008 году
Программа Intel «Путь к успеху» Итоги развития программы в 2008 году Стиль рококо. Художественное направление XVII – XVIII веков
Стиль рококо. Художественное направление XVII – XVIII веков Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие.
Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие. Инженер по гарантии. Шаблон документа
Инженер по гарантии. Шаблон документа МЕЛЬНИЦЫ Новейшая разработка в технологии ультратонкого измельчения
МЕЛЬНИЦЫ Новейшая разработка в технологии ультратонкого измельчения Комитет государственного имущества и приватизации Министерства финансов Республики Казахстан (КГИП)
Комитет государственного имущества и приватизации Министерства финансов Республики Казахстан (КГИП) Лекарственные препараты действующие на собирательные трубки
Лекарственные препараты действующие на собирательные трубки  Участник : Тугумбаев Алибек Айтуллаевич Открытие автокинотеатра «Sky cinema» в г. Астана.
Участник : Тугумбаев Алибек Айтуллаевич Открытие автокинотеатра «Sky cinema» в г. Астана. Гуманизм и новая наука
Гуманизм и новая наука Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор
Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор Общие принципы составления программ инфузионной терапии (ИТ) у детей Обедин А.Н. Ставрополь 2004
Общие принципы составления программ инфузионной терапии (ИТ) у детей Обедин А.Н. Ставрополь 2004 Удивительная вода
Удивительная вода Психология цвета
Психология цвета Техническая эксплуатация судовых АКБ
Техническая эксплуатация судовых АКБ Презентация на тему Математическая логика
Презентация на тему Математическая логика Организационно-правовые основы деятельности любительских объединений. Тема 6
Организационно-правовые основы деятельности любительских объединений. Тема 6 Создание республиканской медицинской информационной системы (РМИС)
Создание республиканской медицинской информационной системы (РМИС) Как правильно ставить цели и достигать их
Как правильно ставить цели и достигать их Оборотные средства предприятия
Оборотные средства предприятия