Математические парадоксы

Содержание
Разрезанный треугольник
Исчезающий квадрат
Парадокс маляра
Парадокс Банаха — Тарского
Танцующие человечки
«Точка – царица геометрии»
“Графическая капля”
“Четырёхугольная кругообразность”
“Цилиндрическое направление”
“Бесподобное подобие”
“Пробуждение эпитрохоиды”
“Единство функциональной зависимости”

Задача о разрезанном треугольнике (частях треугольника)

Условие
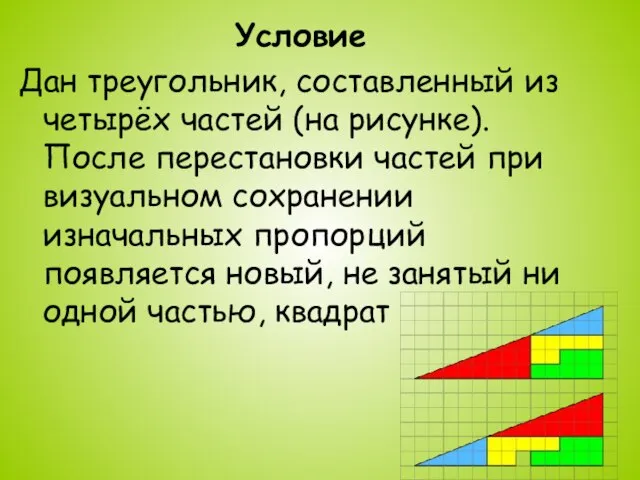
Дан треугольник, составленный из четырёх частей (на рисунке). После перестановки частей при визуальном сохранении изначальных пропорций появляется новый, не занятый ни одной частью, квадрат

Решение
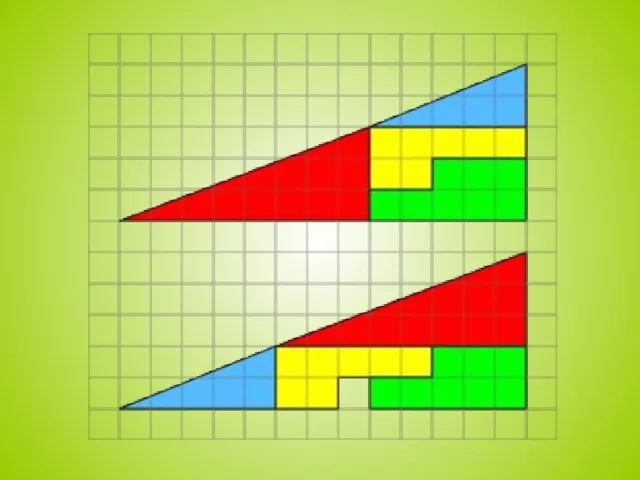
Секрет в том, что синий и красный треугольники имеют неравные углы, что визуально незаметно из-за слишком малой разницы. Поэтому на первом рисунке создаётся излом внутрь, а на втором — наружу. Это легко проверить наложением и вычислениями.
Площадь каждого треугольника 13×5 не равна площади частей, из которых они составлены.

Действительно, общая площадь четырёх частей (жёлтой, красной, синей и зелёной) равна 32 кв. ед., а площадь треугольника 13×5 равна 32,5 кв. ед. Отношение длин катетов синего треугольника 5:2, а красного — 8:3, поэтому эти треугольники не являются подобными, а значит, имеют разные углы. Гипотенузы в обоих треугольниках 13×5 на самом деле является ломаными линиями. Если наложить треугольники 13×5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь.

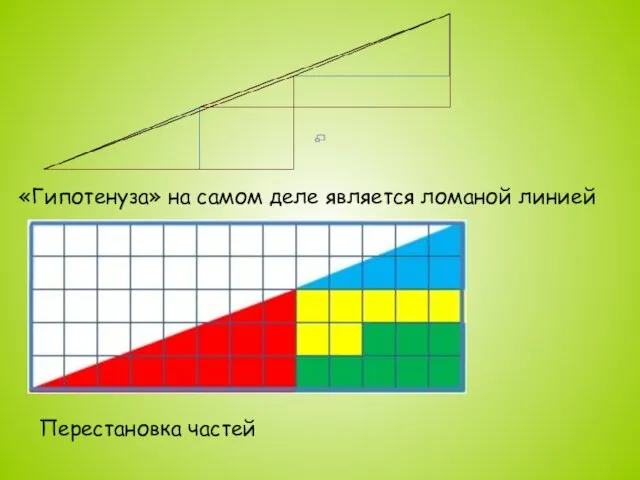
«Гипотенуза» на самом деле является ломаной линией
Перестановка частей

Исчезающий квадрат
В другой головоломке, основанная на таком же принципе, большой квадрат составлен из четырёх четырёхугольников и маленького квадрата. Если четырёхугольники развернуть, то они заполнят площадь, занимаемую маленьким квадратом, хотя площадь большого квадрата визуально не изменится.
Этот парадокс объясняется тем, что сторона нового большого квадрата немного меньше, чем сторона того, который был в самом начале. Если длина стороны большого квадрата a и θ — угол между двумя противоположными сторонами в четырёхугольнике, то площадь большого квадрата после перестановки частей изменится в sec2θ − 1 раз. При , разность между площадями составляет приблизительно 0.8%.

Маленький квадрат «исчезает» при перестановке частей

Парадокс маляра
Парадокс маляра́ — математический парадокс, утверждающий, что фигуру с бесконечной площадью поверхности можно окрасить конечным количеством краски.

Разрешение парадокса
Утверждение «для того, чтобы покрасить фигуру бесконечной площади, необходимо бесконечное количество краски» исходит из того, что фигура покрывается слоем краски одинаковой толщины.
Предлагаемый же способ окраски предполагает, что каждый следующий сегмент будет покрыт всё более тонким слоем, так что бесконечная сумма объёмов краски, ушедших на каждый сегмент площадью в 1 см², будет сходиться к конечному значению.

Парадокс Банаха — Тарского
Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.
! Любые два ограниченных подмножества Евклидова пространства с непустой внутренностью являются равносоставленными.

Танцующие человечки
Танцующие человечки это замечательная оптическая иллюзия, в которой используется эффект движения. Просто начните рассматривать этих человечков. Они очень любят, когда их рассматривают. В ответ на это, они пускаются в пляс и начинают исполнять весьма необычный танец.
Надеюсь, что пластика их движений не оставит вас равнодушными. И помните, человечки станут неподвижными сразу после того, как только вы перестанете их рассматривать!

«Точка – царица геометрии»
Используется для вводной беседы по геометрическому материалу в 5 классе (“Точка. Прямая линия”) и в 7 классе (“Начальные геометрические сведения”).

“Графическая капля”
Используется при изучении темы “Графики функций” в 9 классе.

“Четырёхугольная кругообразность”
Используется для изучения темпо геометрии в 8 классе “Четырехугольники” и “Вписчанные и описанные четырёхугольники”.

“Цилиндрическое направление”
Используется в 8-ом и 9-ом классах для изучения темы “Вектор”.

“Бесподобное подобие”
Используется на уроках геометрии в 8 классе при изучении темы “Подобные треугольники”.

“Пробуждение эпитрохоиды”
Используется на уроках в 9 классе при изучении темы “Уравнение окружности”.

“Единство функциональной зависимости”
Используется в 9–11 классах при изучении тригонометрических функций.

Вывод:
Я заметила, что в мире есть множество парадоксов, стоит лишь повнимательней посмотреть. Так же у меня появился любимый парадокс:
« Танцующие человечки». Я не подозревала, что математику можно изучать с помощью красочных картинок.