Содержание
- 2. 2·2=5 ?!
- 3. 4:4=5:5 4(1:1)=5(1:1) 4=5, или 2·2=5
- 4. умышленно ложное умозаключение, которое имеет видимость правильного. Софизм (от греч. σόφισμα, «мастерство, умение, хитрая выдумка, уловка,
- 5. В Древней Греции развитие искусства ведения дискуссий нередко приводило к изобретению хитроумных «доказательств» неверных утверждений. Такие
- 6. Цель моей работы - выявить основные приёмы, используемые для составления математических софизмов; классифицировать ошибки, допускаемые в
- 7. Типичные ошибки 1. Запрещённые действия: деление на ноль. 2. Неправильное вынесение общего множителя за скобки в
- 8. 9кг=9000000г ?!
- 9. 3кг=3000г 3 ² кг=3000 ² г => 9кг=9000000г
- 10. 8=2 ?!
- 11. (8-5) и (2-5) 3 и -3 3² и (-3)² 3²=9= (-3)² 9=9 Значит 8=2
- 12. 5=6 ?!
- 13. 65+130-195=78+156-234 5(13+26-39)=6(13+26-39) Значит 5=6
- 14. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но может пригодиться и в
- 16. Скачать презентацию

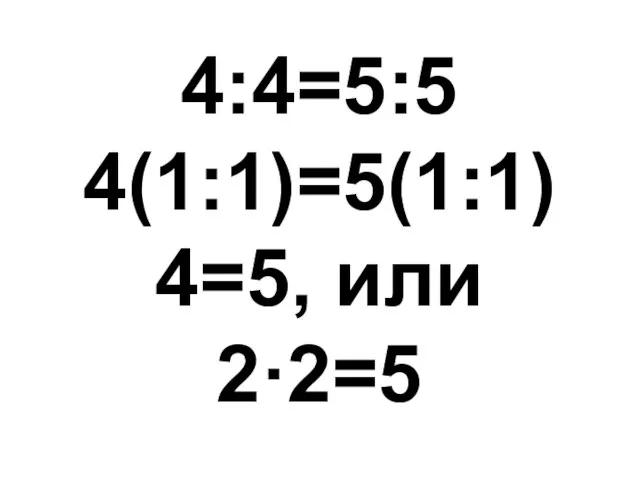





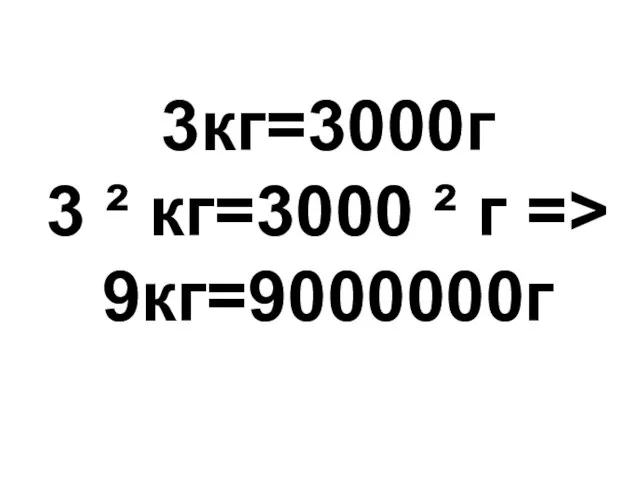
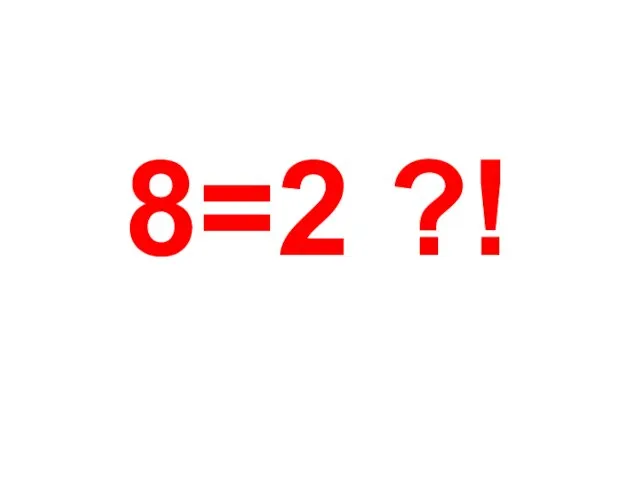
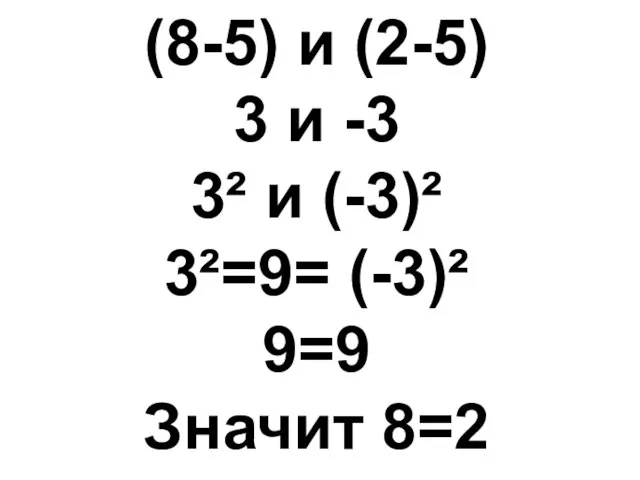
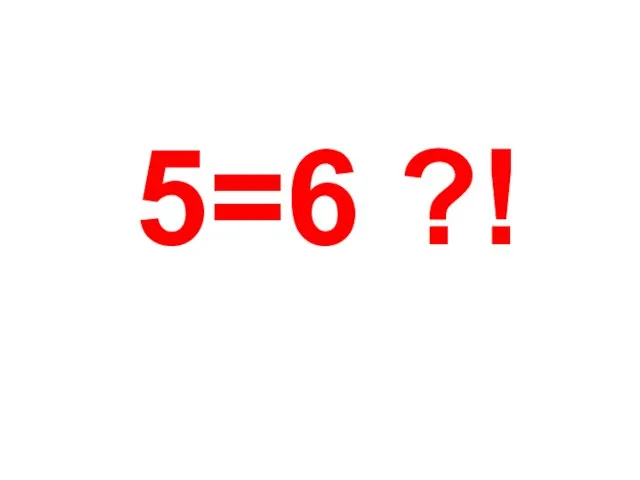


 архитектура эпохи возрождения
архитектура эпохи возрождения Систематика: RFID-решения для вашего бизнеса
Систематика: RFID-решения для вашего бизнеса Знатоки прав. Всероссийский День правовой помощи детям викторина
Знатоки прав. Всероссийский День правовой помощи детям викторина Санаторий Сосновый бор - филиал АО РЖД-здоровье. Кировская область
Санаторий Сосновый бор - филиал АО РЖД-здоровье. Кировская область Основы графической грамоты
Основы графической грамоты Номенклатура дел
Номенклатура дел флагман мирового производства клинкера
флагман мирового производства клинкера Виды промежуточных колонн в конструкции скважины
Виды промежуточных колонн в конструкции скважины Тропы
Тропы США в XIX веке
США в XIX веке Направление нетрадиционной энергетики, основанное на непосредственном использовании солнечного излучения для получения энергии
Направление нетрадиционной энергетики, основанное на непосредственном использовании солнечного излучения для получения энергии Сказочный образ в картинах В.Васнецова.
Сказочный образ в картинах В.Васнецова. SMS Alert Gateway Техническая информация
SMS Alert Gateway Техническая информация Очень краткий гид по ВКР
Очень краткий гид по ВКР Проект “Диванный Trip”
Проект “Диванный Trip” Оценка ценных бумаг. Тема № 8
Оценка ценных бумаг. Тема № 8 Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм
Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм Mon animal
Mon animal Презентація
Презентація Переход на новые образовательные стандарты обучения в начальной школе
Переход на новые образовательные стандарты обучения в начальной школе Бирюза
Бирюза Опыт работы начальной школы
Опыт работы начальной школы Политические основы конституционного строя
Политические основы конституционного строя Реформы Петра I
Реформы Петра I МОУ СОШ № 4 . г. Всеволожск Ленинградская область Тема. Дисциплина Ученица 7 класса «Б» Матвейчук Антонина Учитель Потапова О.Н.
МОУ СОШ № 4 . г. Всеволожск Ленинградская область Тема. Дисциплина Ученица 7 класса «Б» Матвейчук Антонина Учитель Потапова О.Н. Sillamäe Vanalinna Kool 2.03.2011 Sofya Shesterneva «II мировая война в цифрах»
Sillamäe Vanalinna Kool 2.03.2011 Sofya Shesterneva «II мировая война в цифрах» Безопасность работы и конфиденциальность информации в АСУ РСО. - презентация
Безопасность работы и конфиденциальность информации в АСУ РСО. - презентация Базовий сметанний соус
Базовий сметанний соус