Слайд 21. О линейных алгебраических структурах
Значительная часть истории развития естественных наук

пред-ставляет собой летопись непрерывного стремления челове-чества к обобщению понятий, которые позволили бы предста-вить действительной мир в математических терминах. В исто-рии развития социальных наук (особенно экономических) в последнее время также наблюдаются определенные попытки выдвижения коли-чественно обоснованных теорий, использующих математические ме-тоды. Чтобы иллюстрировать математически некоторые законы дейст-вительного мира, необходимо создать соответствующие математи-ческие модели относительно одной или большего числа рассмат-риваемых параметров (переменных).
Слайд 3
Целью такой модели может быть, например, наилучшее распределение имеющегося объема финансовых

средств банка среди нескольких объектов инвестирования, при-носящих разную доходность, с целью получения наиболь-шей суммарной прибыли, или наилучшая организация гру-зоперевозок транспортной фирмой внутри города, с целью обеспечения наименьшего пробега машин порожняком и выполнения всех заявок клиентов в срок и в полном объеме.
Слайд 4Слайд №3
Следует отметить, что сформированная математическая мо-дель для конкретного рассматриваемого процесса или

объекта может быть достаточно сложной для ее математического ана-лиза и тогда необходимы более упрощенные ее модификации. Причем, в некоторых случаях такие упрощенные модели могут с достаточно высокой степенью точности соответствовать опи-сываемому процессу или объекту. В других случаях доступные нам математические модели могут давать значения решений, отличающиеся более чем на 100% от результатов действи-тельных физических измерений.
Слайд 5Таким образом, фактически, мы ожидаем, что сформи-рованная математическая модель будет служить для

следующих основных целей: количественной оценки вы-бранных параметров для рассматриваемого процесса или объекта; предсказанию изменения их значений в будущем, т.е. для прогнозирования; влиянию на изменение значений выбранных показателей оценки качества рассматрива-емых процессов или объектов, т.е. управления ими. При этом точность, требуемая от такой модели, опреде-ляется конечной целью, для которой она создавалась.
Слайд 6
Линейность для различных математических структур представляет собой весьма общее понятие:

существуют линейные алгебраические уравнения, линейные обыкно-венные дифференциальные уравнения, т.е. уравнения от-носительно производных функций от выбранных пере-менных и т.д.
Все линейные модели обладают свойствами адди-тивности и однородности.
Слайд 7
С математической точки зрения, линейные модели имеют серьезные преимущества перед всеми

остальными – нелиней-ными моделями. При этом, в случае нелинейных систем при применении математических методов почти всегда возникают трудности при их аналитическом (формульном) изучении и часто возникают потребности в применении компьютеров даже при ре-шении простейших задач поставленных в рамках этих моделей, т.е. требуется разработка сложных численных (приближенных) методов и алгоритмов для решения задач, сформулированных в рамках таких моделей.
Слайд 8
При этом во многих случаях даже мощные компьютеры оказы-ваются бесполезными для

исследования таких систем. С другой стороны, часто значительно легче работать с линейными моде-лями и получать аналитические и численные решения, пред-ставляющие интерес для рассматриваемых практических задач.
Слайд 9
Оба эти фактора – доступность для исследования и достаточная точность приближения

к действительному миру – делают линейные модели наиболее широко приме-нимым математическим аппаратом в естественных и соци-альных науках. Причем существуют математические методы, позволяющие при математическом моделировании рассмат-ривать только наиболее значимые для рассматриваемого про-цесса параметры и использовать только линейные матема-тические структуры, которые являются достаточно адекватными рассматриваемым процессам и позволяют получать прием-лемые для практики результаты решения соответствующих кон-кретных практических задач.
Слайд 10
При этом, под адекватностью математической модели исходному процессу понимают такую соответствующую

ему математическую модель, что решение чисто математи-ческих задач, сформированных в рамках этой модели, поз-воляет получать приемлемые количественные резуль-таты для конкретных практических задач, связанных с данным процессом.
Тогда возникает вопрос: «Что понимается под линейной операцией и чем она характеризуется?».
Слайд 11 Можно дать следующее формальное определение понятия линейной операции.

Слайд 15
Можно сказать, что алгебраические структуры, порожденные линейными операциями над множествами

элементов, в которых определены операции сложения элементов и умножения их на действительное число, называются линейными алгебраи-ческими структурами.
Предметом для линейных алгебраических структур является изучение таких элементов, как вектора, матрицы, опре-делители, линейные алгебраические уравнения и др., изучение связанных с ними свойств и свойств порожденных ими структур (например, систем линейных алгебраических уравнений, систем линейных алгебраических неравенств, линейных пространств и др.), а также изучение связанных с ними математических задач и методов их решения.
Слайд 16 Основными задачами для линейных алгебраических структур являются следующие:
изучения свойств линейных

алгебраических структур;
выяснения существования решений задач, порожден-ных линейными алгебраическими структурами;
в случае существования решений таких задач, разработка методов нахождения их решений;
разработка и изучение алгоритмов для реализации нахождения решений таких задач, например, на компьютере и др.
Слайд 17Следует также отметить, что разработанный аппарат для линейных алгебраических структур, т.е. элементы

рассматри-ваемых в ней структур и порожденные ими объекты и свойства, имеют широкое и важное применение в математическом моде-лировании, также при разработке и реализации различных алгоритмов для решения задач в различных математических моделях, т.е. в моделировании и решении конкретных приклад-ных, в том числе и экономических задач, например, на компьютерах.
Слайд 18
2. Методология математического и компьютерного моделирования
Существуют различные подходы и

принципы экономико-математического и компьютерного моделирования функ-ционирования сложных экономических систем (объектов) и ниже предлагается один из таких возможных под-ходов.
Введем в рассмотрение следующее основное опре-деление.
Слайд 19
Под общей многоуровневой иерархической динамической экономической системой (объектом исследования), управ-ляемой основным

субъектом управления, будем понимать совокупность ее внутренних частей (подсистем), состоящих из соответствующих им объектов и элементов, в которых рассматриваются процессы, управляемые соответствующими субъектами управления, имеющими собственные сферы интересов в условиях иерархической подчиненности основному субъекту управления, функционирующую в конкретной среде при наличии неопределенности, которую в целом можно раз-личать среди других систем и в своем составе она имеет:
Слайд 20
входные информационные устройства и средства (устройства ввода данных), сопряженные с

ее объектами или элементами;
устройства и средства для хранения данных (запоми-нающие устройства), сопряженные с ее объектами или элементами;
устройства и средства, позволяющие реализовать математические, логические и иные операции для анализа и обработки данных, сопряженные с ее объек-тами или элементами;
выходные информационные устройства и средства (устройства вывода данных), сопряженные с ее объек-тами или элементами;
Слайд 21
устройства и средства для реализации управляющих связей между ее объектами

или элементами;
устройства и средства для реализации информа-ционных связей между ее объектами или элементами;
устройства и средства, позволяющие реализовать выбранные системы кодирования и декодирования дан-ных (например, в двоичной системе счисления), сопря-женные с ее объектами или элементами.
Слайд 22Слайд №21
Тогда основные этапы математического и компьютерного моделирования различных задач

проектирования и организационного управления в сложных многоуровневых иерархических динами-ческих экономических системах, функционирующих в условиях неопределенности, можно представить в виде реализации следующей последовательности основ-ных этапов.
Слайд 23
В рассматриваемой системе выделяется основной субъект управления рассматриваемыми в ней

процессами, контролирующий основной уровень управления, и выделяются ее части (подсистемы) – другие (подчиненные) уровни управления, которые могут находиться в сфере интересов других (подчиненных) управляющих субъек-тов (если таковые присутствуют), находящихся в условиях иерархической подчиненности основному субъекту управления.
Слайд 24В рассматриваемой системе и ее подсистемах выде-ляются наиболее значимые для их исследования

соот-ветствующие им параметры состояния, характеризую-щие исследуемые в системе процессы в фиксированный момент времени (если рассматривается динамический процесс, как наиболее общий) и соответствующие им ограничения.
Слайд 25 Выделяются параметры управления процессами в системе в целом и подсистемах, которые

могут изменяться по ходу реализации конкретного процесса в зависимости (по желанию и возможностям) от выбора соответствующего управляющего субъекта и соответ-ствующие им ограничения (физической реализуе-мости, технические, экономические и др.).
Слайд 26 Выделяются неуправляемые параметры для рас-сматриваемых в системе в целом и подсистемах

процессов (неконтролируемые конкретным управля-ющим субъектом, или учитывающие влияние конкрет-ной внешней среды или описывающие погрешности моделирования процессов), которые изменяются вне зависимости от желания и возможностей конкретного управляющего субъекта и соответствующие им ограничения.
Слайд 27 Для каждой из подсистем и для системы в целом определяются параметры

процессов, характеризую-щие их структуру и внутренние связи между объектами или элементами системы.
Формируются условия информационного обеспечения для каждого из управляющих субъектов, которым под-чиняются соответствующие уровни управления, информаци-онные и управляющие связи между ними и условия иерархической подчиненности при принятии управлен-ческих решений субъектами управления, а также соответ-ствующие им ограничения.
Слайд 28Для каждой из подсистем рассматриваемой системы формируются критерии (в частном случае −

один критерий), позволяющие оценивать качество функционирования этой подсистемы и формиру-ются также соответствующие критерии (или критерий), которые позволяют оценивать качество функционирования исследуемой системы в целом.
Слайд 29 Для каждой подсистемы, на основании выбранных соот-ветствующих критериев качества функционирования соответ-ствующих

ей процессов, формируются цели, достижение которых является наилучшим или приемлемым для соответ-ствующего управляющего субъекта, и аналогично формиру-ются соответствующие цели и для субъекта, управ-ляющего рассматриваемыми процессами в системе в целом, которые в совокупности соответствуют сформиро-ванным критериям качества для рассматриваемых процессов.
Слайд 30На основании предыдущих этапов определяется матема-тический и технический инструментарий моделирова-ния и формируются

математические модели для каждой из подсистем и рассматриваемой системы в целом, учиты-вающие соответствующие им процессы, которые в какой-то мере адекватны реальным процессам и позволяют анализировать и исследовать их имеющимися сред-ствами и в приемлемое время.
Слайд 31 Для сформированных задач разрабатываются математические методы их решения в форме реализации

соответствующих последовательнос-тей логических, математических и иных операций.
В математических моделях процессов, исследуемых в подсистемах и рассматриваемой системе в целом, фор-мируются математические задачи, соответству-ющие набору имеющихся реальных задач и процессов.
Слайд 32 Для каждого из математических методов решения задач разрабатываются соответствующие им численные

алгоритмы (также в форме логических, математических и иных операций), позволяющие реализовать моделиро-вание решения этих задач (например, на компьютере) с целью получения приемлемых результатов.
С помощью программных и технических средств, на базе разработанных численных алгоритмов, осуществляется реализация математического и компьютерного моде-лирования исследуемых процессов в подсистемах и в рассматриваемой системе в целом.
Слайд 33 Рассматриваемая методология математического и компьютерного моделирования различных экономических систем и процессов

в них может применяться как в целом, состоящая из всех этапов (для достаточно сложных экономических систем и процессов), так и частично − в зависимости от основных целей моделирования и струк-туры конкретного исследуемого экономического процесса.
Сделаем важное замечание – с помощью такого подхода можно реализовать математическое и компьютерное мо-делирование различных процессов в технике, экономике, медицине и в др. предметных областях деятельности человека.
Слайд 34 Отметим, что реальная исследуемая экономическая система может иметь достаточно большое количество

значимых пара-метров (состояния, управляемых, неуправляемых и др.), ха-рактеризующих ее функционирование. Тогда для анализа и исследо-вания соответствующих ей процессов, выделяют только наиболее существенные (с точки зрения выбранных критериев качества процессов) параметры, описывающие ее подсистемы и систе-му в целом, т.е. снижают размерность соответствующих ма-тематических моделей, формируя упрощенный образ рас-сматриваемой системы. Затем разрабатывают математичес-кие модели подсистем и системы в целом, которые являются определенной абстракцией, приемлемой для исследования соответствующих им реальных процессов.
Слайд 35 Образно, сформированные математические модели по отно-шению к реальной экономической системе и

ее подсистемам, учитывающие соответствующие им процессы, можно изобразить следующим образом.
Слайд 36 При этом математическая модель системы находится «вне реальной системы», а не

содержится в ней, т.к. она может быть использована и для исследования других реальных систем и соответствующих им процессов. Так, например, математические модели могут быть такими мате-матическими структурами, которые могут применяться для моде-лирования и исследования реальных систем и соответствующих им практических задач, как в области экономики, так и в области медицины.
Слайд 373. Реализация методологии математического
и компьютерного моделирования
Приведенную выше последовательность основных

этапов экономико-математического и компьютерного моделирования на практике можно реализовать в форме следующих основных блоков.
I. Для выделенных значимых параметров состояния системы, структурных параметров, управляемых и неуправляемых па-раметров, в рамках выбранного математического инстру-ментария, формируется математическая модель, описы-вающая стационарные или динамические процессы, соответ-ствующие исследуемым процессам для подсистем и системы в целом в форме:
Слайд 381) алгебраических или операторных соотношений (детерми-нированных или стохастических, в случае, если объект

стационарный);
2) алгебраических рекуррентных соотношений, дифферен-циальных или операторных динамических соотношений (детер-минированных или стохастических, в случае, если процесс ди-намический) и др.
При этом соотношения будут стохастическими, если присут-ствуют неопределенные параметры, для которых известны их вероятностные характеристики.
Слайд 39II. Для математических моделей подсистем и системы в целом, формируются имеющиеся управляющие

связи, условия иерархической подчиненности и информационного обеспе-чения для соответствующих субъектов, управляющих подсисте-мами и для субъекта, управляющего системой в целом, в сле-дующем виде:
∙ информационных сигналов, являющихся «выходными данными» или значениями функционального (операторного) преобразования (соотношения), определенного на «входных данных» – параметрах состояния, структурных параметрах, управляемых или неуправляемых параметрах, при наличии погрешностей (ошибок) измерений (эти преобразования мо-гут иметь вид, например, действительных функций многих переменных, дифференциальных или операторных соотно-шений, описывающих уравнение измерений информацион-ных сигналов).
Слайд 40III. Для каждой из подсистем рассматриваемой системы и для системы в целом

формируются критерии качества функци-онирования соответствующих им процессов, которые в случае наличия, например, одного критерия, имеют вид дей-ствительной функции одной или нескольких действительных переменных, а в случае наличия нескольких критериев (наибо-лее общий случай) − критерием качества является набор функций (или векторная функция), состоящий из набора дей-ствительных функций нескольких действительных переменных (в таких случаях говорят, что имеется векторный критерий качества или векторный показатель функционирования процес-са в конкретной подсистеме или в системе в целом – наиболее сложный показатель).
Слайд 41IV. Для выделенных подсистем и системы в целом, а также для сформированных

критериев качества функционирования под-систем и системы в целом, формируются цели, которые прес-ледуют соответствующие управляющие субъекты, имеющие обычно форму достижения максимальных или ми-нимальных значений соответствующих критериев (причем, для векторных критериев необходимо использовать аналогичные им понятия, с учетом специфики задачи).
Слайд 42V. Для параметров состояния, структурных параметров, управляемых и неуправляемых параметров, всех априори

неопределенных параметров системы (погрешностей модели-рования подсистем и системы в целом, ошибок измерений информационных сигналов, неопределенностей моделирования критериев качества рассматриваемых процессов и др.) форми-руются ограничения на их изменения, отражающие имеющие-ся реальные ограничения (физические, химические, биологи-ческие, экономические и др.) в форме:
Слайд 431) алгебраических уравнений или неравенств (детерми-нированных или стохастических);
2) дифференциальных уравнений или неравенств

(детерми-нированных или стохастических);
3) операторных уравнений или неравенств (детерминированных или стохастических) или др.
При этом важна достаточная адекватность ограни-чений в математической модели, имеющимся реальным ограничениям.
Слайд 44VI. Для сформированных в блоках I – V математических моделей, образующих в

комплексе математическую модель ис-следуемых процессов в рассматриваемой системе, формулиру-ются, например, математические задачи оптимизации гарантированного результата (позволяющие учитывать наличие неопределенности или конфликта в рассматриваемой системе), соответствующие реальным практическим задачам и для сформулированных задач разрабатываются математи-ческие методы их решения [см., например, 1,2], а также численные алгоритмы (например, в форме реализации конеч-ных последовательностей логических, математических и иных операций), позволяющие организовать и реализовать модели-рование решения этих задач, например, на компьютере.
Слайд 45VII. На основе сформированных в блоке VI алгоритмов разрабатывается и формируется программное

и техни-ческое обеспечение или используется стандартное, по-зволяющее реализовать процесс моделирования исходной системы и решения сформулированных в рамках ее задач, соответствующих исходным реальным задачам.
Слайд 46VIII. С помощью сформированных программных и технических средств реализуется, например, компьютерное моделиро-вание

исследуемых процессов для рассматриваемой системы. При этом в случае получения приемлемых результатов модели-рования, согласующихся с известными практическими резуль-татами, моделирование считается приемлемым для решения практических задач. В случае, если отсутствуют приемлемые результаты при компьютерном моделировании, то процесс формирования математической модели системы корректируется, начиная с блока I до блока VII, и затем повторяется до получения приемлемых результатов компьютерного модели-рования, согласующихся с практическими результатами реали-зации исследуемых процессов в рассматриваемой системе.
Слайд 47 Следует отметить, что процесс математического и компьютерного моделирования (в общем случае)

является циклическим. При его реализации изменяются как рассматриваемые параметры исследуемой системы, так и используемые математические и технические средства.
Слайд 48 Таким образом, на основании вышеизложенного, можно сделать общий вывод, что для

реализации математического и компью-терного моделирования сложных экономических процессов в форме многоуровневых иерархических динамических систем, необходимо изучение методов формирования и анализа таких моделей, методов и алгоритмов решения различных задач, которые могут быть сформулированы в рамках таких моделей (например, задач оптимизации гарантированного результата), а также исследование различных математических операций, которые позволяют организовать реализацию этих алгорит-мов, например, с помощью компьютера и современных инфор-мационных технологий, имеющимися или сформированными техническими и программными средствами.
Слайд 49 Тогда можно сделать вывод (более конкретный), что предметом математического и компьютерного

модели-рования является изучение принципов и методов построения различных математических моделей реальных систем и со-ответствующих им процессов, анализ этих моделей, изучение методов и разработка алгоритмов решения различных задач, которые могут быть сформулированы в рамках таких моделей, а также исследование различных логических, математических и иных операций, которые позволяют организовать реализацию этих алгоритмов, например, с помощью компьютера, имею-щимися или сформированными программными и техническими средствами.
Слайд 504. Модели математического программирования
Одной из наиболее общих и широко используемых в

математическом моделировании, в частности, в эко-номико-математическом моделировании, является модель нелинейного математического программиро-вания, которая может быть описана следующим образом.
Слайд 54 Задача 1 называется задачей нелинейного мате-матического программирования (НМП).
Следует отметить, что

задача 1 является наиболее общей среди так называемых оптимизационных задач на условный экстремум, т.е. задач, в которых требуется находить максимум или минимум заданной целевой функции на заданном множестве, которые формируются из каких-то классов функций и множеств.
Слайд 55 К задаче 1 НМП (как математической модели) сводятся различные и важные

практические задачи, например, в области техники, экономики, биологии, медицины и др.
Слайд 57 Для решения задач ЛМП разработан очень эффективный метод – симплекс-метод в

случае, если система линейных неравенств, порождающая ограничения (1.2), является сов-местной. В разработку этого метода и исследование раз-личных свойств задач ЛМП внесли большой вклад выда-ющиеся математики Л.В. Канторович, Дж. Б. Данциг, Т.К. Купманс, Дж. Фон Нейман, Г.У. Кун, А.У. Таккер, а Л.В. Кан-торович и Т.К. Купманс получили за свои работы в этой области Нобелевскую премию по экономике.
Слайд 58 При этом для задач ЛМП разработаны также другие методы решения, которые

могут быть использованы для моделирования решения различных практических задач, в том числе, и в экономике.
Если в рассмотренных задачах математического программи-рования множество Х, ограничивающее множество всех допус-тимых состояний рассматриваемой системы или объекта является целочисленным, то такие задачи называются задача-ми целочисленного математического программирования (ЦМП). Для решения задач ЦМП также разработаны достаточно эффективные методы (например, направленного перебора, «ветвей и границ» и др.), допускающие численную реализацию на компьютере.
Слайд 595. Пример экономико-математического моделирования
Пример 1.
Пусть имеется производственное предприятие, которое выпускает

два вида красок − краски типа I и II. При этом стоимость 1 т краски типа I на рынке 3000 $, а стоимость 1 т краски типа II – 5000 $. Для производства 1 т краски типа I требуется 2 т сырья вида А и 1 т сырья вида В, а для производства 1 т краски типа II требуется 1 т сырья А и 2 т сырья В. Причем для производства каждой из красок требуется только эти две компоненты сырья. На данном предприятии имеются условия для хранения суточного запаса сырья вида А в объеме не превышающем 25 т, а сырья вида В − не более 30 т.
Слайд 60 Тогда эти данные можно свести в следующую таблицу.
Таблица 1
Из проведенных
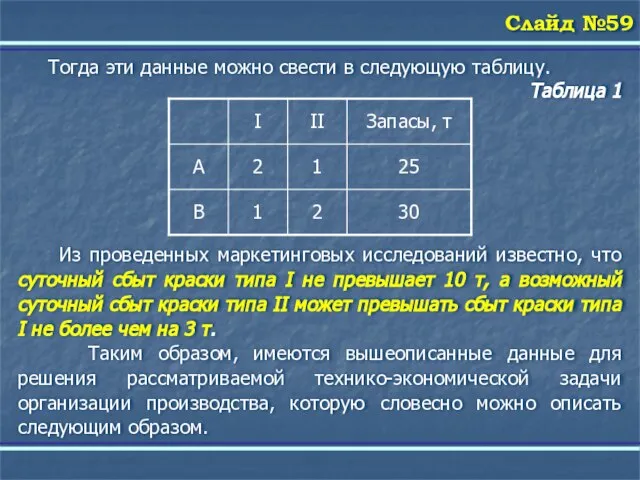
маркетинговых исследований известно, что суточный сбыт краски типа I не превышает 10 т, а возможный суточный сбыт краски типа II может превышать сбыт краски типа I не более чем на 3 т.
Таким образом, имеются вышеописанные данные для решения рассматриваемой технико-экономической задачи организации производства, которую словесно можно описать следующим образом.
Слайд 61 Руководству предприятия требуется так органи-зовать суточное производство красок типа I и

II, чтобы получить максимальный суточный доход от реализации обоих типов краски, причем требуется учитывать имеющиеся суточные складские запасы сырья и не зато-вариться готовой продукцией, т.е. учитывать суточный рыночный спрос.
Это – словесное описание задачи производственного и организационного управления.
Слайд 62 В принципе эту задачу можно решать перебором возмож-ных вариантов различных суточных

объемов производ-ства краски обоих типов при учете имеющегося склад-ского ресурса и спроса на краску. При достаточно большой номенклатуре производства и используемого сырья, такой способ нахождения решения может привести к необозри-мому числу необходимых арифметических операций и не исключено, что мы не сможем найти в приемлемое время существующий наилучший вариант суточного производства объемов красок для получения соответствующего максимально возможного суточного дохода. При этом отметим, что сущест-вует также трудность организации перебора допусти-мых вариантов производства.
Слайд 63 С другой стороны, для рассматриваемой задачи сущест-вует возможность формирования экономико-математи-ческой модели,

которая достаточно адекватна условиям данного производства, хранения, сбыта и позволяет раз-работать эффективные методы решения рассматрива-емой технико-экономической задачи организации произ-водства.
Ниже рассмотрим один из возможных вариантов экономико-математического моделирования.
Слайд 64 Это параметры состояния процесса, которые являются значимыми для данной задачи.

Слайд 72 Для задач линейного математического программирования разработаны эффективные методы нахождения решений –

оптимальных планов и оптимальных значений целевой функции и наиболее эффективным из них, с позиции численной реализации, является так называемый симплекс-метод.
В соответствии с этим, задачу 2 можно решать также симплекс-методом.
Решение задачи 2 при наличии достаточно большого числа переменных (от 10 и более), например, с помощью симплекс-метода, позволяет достичь большого реального эконо-мического эффекта.
Слайд 73 Таким образом, в соответствии с описанной выше методологией математического моделирования, для

фор-мирования экономико-математической модели рас-сматриваемой задачи были использованы только неко-торые этапы: 1) − 6), позволяющие учесть имеющиеся в данной задаче технико-экономические условия.
Слайд 74СПИСОК ЛИТЕРАТУРЫ
Красовский Н.Н., Субботин А.И. Позиционные дифферен-циальные игры. М.: Наука, 1974.
Шориков А.Ф.

Минимаксное оценивание и управление в дискретных динамических системах. Екатеринбург: Изд-во УрГУ, 1997.
Канторович Л.В. Экономический расчет наилучшего использования ресурсов. М.: Изд-во АН СССР, 1959.
Карлин С. Математические методы в теории игр, програм-мировании и экономике. М.: Мир, 1964.
Леонтьев В.В. Исследование структуры американской экономики. М.: Госстатиздат, 1958.
Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем. М.: Мир, 1973.
Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. М.: Наука, 1970.









































































 Полевые сорняки
Полевые сорняки Наглядная агитация отряда № 2
Наглядная агитация отряда № 2 Угроза за спиной
Угроза за спиной DIPLOMATIC SERVICE
DIPLOMATIC SERVICE Жизнь как деяние
Жизнь как деяние Сохранить природу-сохранить жизнь.
Сохранить природу-сохранить жизнь. Модернізація причального контейнерного перевантажувача вантажопідйомністю 50 т
Модернізація причального контейнерного перевантажувача вантажопідйомністю 50 т Группа компаний МАСКОМ Компания Digital Security ТЕМА: Выполнение требований 152 ФЗ и PCI DSS в современных информационных системах - эффект с
Группа компаний МАСКОМ Компания Digital Security ТЕМА: Выполнение требований 152 ФЗ и PCI DSS в современных информационных системах - эффект с Кухня. Стеллажи
Кухня. Стеллажи Организация обучения по подготовке аудиторов в учебных центрах
Организация обучения по подготовке аудиторов в учебных центрах ОРУЖИЕ ПОБЕДЫ
ОРУЖИЕ ПОБЕДЫ таблица на 2
таблица на 2 Презентация на тему методическая система
Презентация на тему методическая система  Кто хочет стать миллионером? 8 класс
Кто хочет стать миллионером? 8 класс ИНФОРМАЦИЯ О КОМПАНИИ
ИНФОРМАЦИЯ О КОМПАНИИ Вода – особенная жидкость
Вода – особенная жидкость Эти загадочные пирамиды
Эти загадочные пирамиды Исследование силовой подготовки девушек и женщин, занимающихся фитнесом
Исследование силовой подготовки девушек и женщин, занимающихся фитнесом Яблочно-молочное брожение (ЯМБ)
Яблочно-молочное брожение (ЯМБ) «Платок в квадрате» Музей истории русского платка и шали (Московская область) Номинация «Партнерские музейные проекты» Руковод
«Платок в квадрате» Музей истории русского платка и шали (Московская область) Номинация «Партнерские музейные проекты» Руковод Фотовыставка Несовместимы дети и война
Фотовыставка Несовместимы дети и война Ценные свойства козьего молока и продуктов из него. 3 класс
Ценные свойства козьего молока и продуктов из него. 3 класс Магазин 5 Элемент
Магазин 5 Элемент Технология и оборудование для изготовления горячей штамповкой номенклатуры деталей типа вилка
Технология и оборудование для изготовления горячей штамповкой номенклатуры деталей типа вилка Инструкция по замене разработки пользователя на сайте «Учительский портал» http://www.uchportal.ru/
Инструкция по замене разработки пользователя на сайте «Учительский портал» http://www.uchportal.ru/ Н и НН в суффиксах имен прилагательных
Н и НН в суффиксах имен прилагательных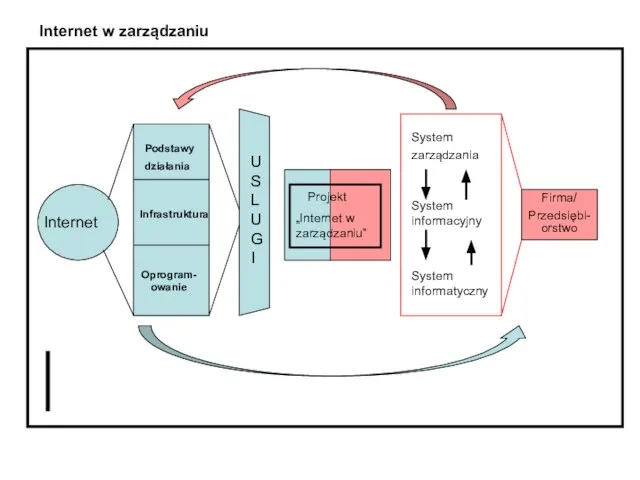 Internet w zarzadzaniu
Internet w zarzadzaniu Музы Сергея Есенина
Музы Сергея Есенина