Математическое описание случайных явлений

Случайные события – это те события, которые при одних и тех же условиях могут произойти, а могут и не произойти.
А = { мне сегодня встретится черная кошка}
Невозможные события – это такие события, которые в данных условиях произойти не могут.
А = { при бросании игрального кубика выпадет семь}
Достоверные события – это те события, которые в данных условиях обязательно произойдут.
А = { при бросании игрального кубика выпадет число, меньше чем семь}

Укажите, какие из следующих событий невозможные, какие – достоверные, какие – случайные:
«Меня завтра вызовут отвечать к доске»
«Летом у меня будут каникулы»
«Баскетбольный мяч попал в кольцо»
«Я брошу игральную кость, и выпадет «шестерка»
«Электрическая лампочка перегорит»
«На морозе вода в стакане замерзнет»
«В Москве завтра произойдет извержение вулкана»

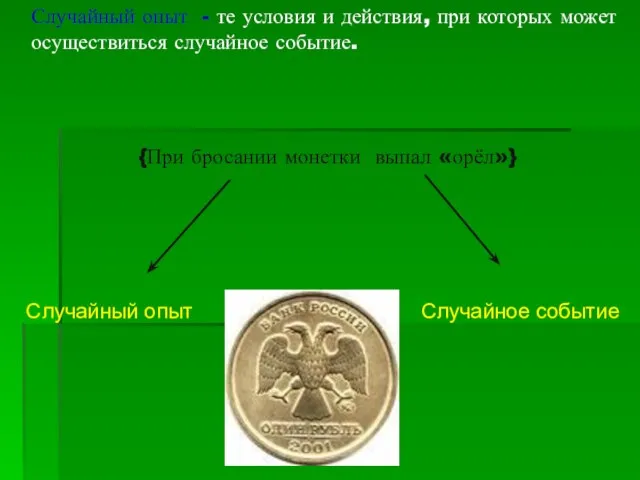
Случайный опыт - те условия и действия, при которых может осуществиться случайное событие.
{При бросании монетки выпал «орёл»}
Случайный опыт
Случайное событие

Укажите, что является случайным опытом, а что – случайным событием:
«В день самоуправления я буду директором школы»
«Футбольный матч закончился победой сборной команд 8 «А» и 8 «Б» классов»
«Я купила лотерейный билет и выиграла»
«Лайнер «Титаник» столкнулся с айсбергом»
«Молния ударила в дерево»

Исходы события
Равновозможные исходы – это все возможные исходы случайного эксперимента, если нет никаких оснований считать один исход вероятнее другого.
Благоприятные для события исходы – это те исходы, которые приводят к наступлению события.

Укажите число возможных исходов эксперимента: 1. Подбрасываем монетку.
2. Вытаскиваем из колоды карт одну.
3. Игральную кость подбрасываем два раза.
Укажите число благоприятных исходов:
1. Выпадет «орёл».
2. Вытаскиваем из колоды карту красной масти.
3. Игральную кость подбрасываем два раза. В результате выпало 7 очков.

Вероятность случайного события
Р = 0 ,
если событие не наступает (невозможное событие);
Р = 1 ,
если событие наступает всегда (достоверное событие)
Р = m / n ,
где m – число, благоприятных исходов;
n - число всех исходов

Найдите вероятность каждого из событий:
1. {При бросании кубика выпало число, меньшее семи}
2. {При бросании кубика выпало пять}
3. {При бросании кубика выпало четное число}
4. {Из слова ВЕРОЯТНОСТЬ случайным образом выбирается одна буква. Какова вероятность того, что она окажется гласной?}

Противоположные события
Событие В называется противоположным к событию А, если оно происходит всякий раз, когда не происходит А и, наоборот.
Например, к событию А={выпало число, большее 5} противоположным будет событие В={выпало число, меньшее или равное 5}

Вероятность противоположного события
Сумма вероятностей противоположных событий равна единице:
Р (А) + Р (В) = 1

Найдите вероятность каждого из событий:
1. {В вазе лежат конфеты – две конфеты «Белочка» и две конфеты «Орбиты». Из вазы, не глядя, берут две конфеты. Какова вероятность того, что взятые конфеты окажутся разного вида?}
2. {Какова вероятность того, что при бросании двух игральных костей кости (1;1), (2;2), (3;3), (4;4), (5;5), }
(6;6) не выпадут?}