Математическое описание случайных явлений (часть 1)

пункт 26. Элементарные события

Пункт 26 №1.
Андрей и Борис решили купить мороженое и встали в очередь. Сколькими способами они могут расположиться друг за другом? Выпишите эти способы.
Обозначим:
Андрея- буквой А, а Бориса- Б.
Друг за другом они могут расположиться только двумя способами
АБ или БА.

Вопрос :
Сколько всего получилось элементарных событий?
Условие
В киоске продаётся три сорта мороженого: сливочное, шоколадное и клубничное. Андрей и Борис покупают по одной порции мороженого.
Пункт 26 №2.

Решение
Рассмотрим все варианты событий какой вкус могут купить Борис и Андрей.
Предположим, что Борис любит только шоколадное мороженное, тогда Андрей может купить любое из трех видов.
Если Борис любит клубничное, то Андрей снова может купить все три вкуса.
То же произойдет и с ванильным мороженным для Бориса.
Но если предположить, что Андрей любит только шоколадное мороженное, то тогда Борис может попробовать все три вкуса. Но это уже есть в нашей таблице.
Ответ: всего получилось 9 элементарных событий.

Пункт 26 №3.
Андрей, Борис и Владимир решили купить мороженое и встали в очередь за покупкой. Сколькими способами они могут расположиться друг за другом? Выпишите все эти способы.
Первый способ решения
Обозначим :
Андрея- буквой А,
Бориса- буквой Б,
Владимира- буквой В.
Следовательно, получается :
АБВ,АВБ, БАВ,БВА,ВАБ,ВБА.
Итого 6 способов.

Пункт 26 №3.
Андрей, Борис и Владимир решили купить мороженое и встали в очередь за покупкой. Сколькими способами они могут расположиться друг за другом? Выпишите все эти способы.
Второй способ решения
Первым может стоять
любой из 3 мальчиков,
следующим любой из 2, оставшийся мальчик будет последним( 1 вариант)
Получим 3!=1·2∙3=6
Итого 6 способов.

Пункт 26 №4.
В ящике четыре детали: две исправные детали а и Ь и две бракованные детали с и d. Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.
cdab не является элементарным событием,
так как все бракованные детали обнаружили
после второго извлечения.
а) Является ли сdаЬ элементарным событием в этом опыте?
б) Какими буквами может заканчиваться запись элементарного события?
запись элементарного события может заканчиваться буквами c или d.

Пункт 26 №4.
В ящике четыре детали: две исправные детали а и Ь и две бракованные детали с и d. Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.
г) Сколько различных элементарных событий записывается тремя буквами?
в) Выпишите все элементарные события этого опыта.
Мы знаем, что запись элементарного события должна заканчиваться буквами c или d. Сначала запишем все события (элементарные и неэлементарные), а потом вычеркнем те, которые заканчиваются на буквы a и b.
Abcd badc cabd dabc
Abdc bacd cadb dacb
Adbс bdca cbad dbac
Adсb bdac cbda dbca
Acbd bcad cdab dcab
Acdb bcda cdba dcba
Посчитаем оставшиеся события : abcd, bdac, cabd, dabc, abdc, bacd, adbc, cbad, dbac, bdac, acbd,bcad, acdb.

Пункт 26 №4.
В ящике четыре детали: две исправные детали а и Ь и две бракованные детали с и d. Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.
г) Сколько различных элементарных событий записывается тремя буквами?
Сначала составим все события:
Вычеркнем неэлементарные:
abc abd acd bcd
acb adb adc bdc
bac bad cad cbd
bca bda cda cdb
cab dba dac dbc
cba dab dca dcb
Остались события: acd, adc, cad, dac, bcd, bdc, cbd, dbc.
Всего: 8

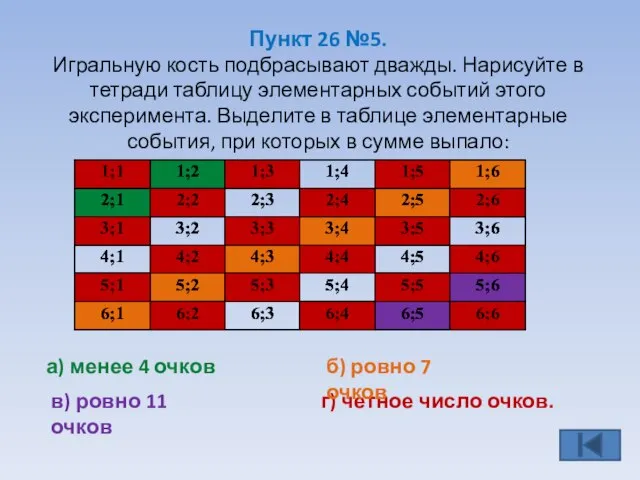
Пункт 26 №5.
Игральную кость подбрасывают дважды. Нарисуйте в тетради таблицу элементарных событий этого эксперимента. Выделите в таблице элементарные события, при которых в сумме выпало:
г) четное число очков.
а) менее 4 очков
б) ровно 7 очков
в) ровно 11 очков

Подбросим монету два раза. Появление двух орлов записывается как ОО. Это одно из элементарных событий этого опыта.
Подбросим монету три раза. Выпишите все элементарные события этого опыта.
Во сколько раз больше число элементарных событий при трёх бросаниях монеты, чем при двух бросаниях монеты?
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 1:
Элементарные события: ОО, РР,ОР, РО.
Опыт 2:
Элементарные события:
ООО,ООР, ОРО, ОРР, РРР, РОО, РОР, РРО.
Опыт 3:
В 2 раза.

* Сколько элементарных событий при четырех бросаниях монеты?
Опыт 4*:
16, т.к. при подбрасывании выпадает 16
разных комбинаций:
2 варианта на первое подбрасывание (О или Р)
2 варианта на второе подбрасывание (О или Р)
2 варианта на третье подбрасывание (О или Р)
2 варианта на четвертое подбрасывание (О или Р) Всего: 2 ∙2 ∙2 ∙2 ∙2=16
* Сколько элементарных событий при десяти бросаниях монеты?
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 5*:
1024, т.к. при подбрасывании выпадает 1024 различных
комбинаций. Это можно узнать, возведя 2 в 10 степень.

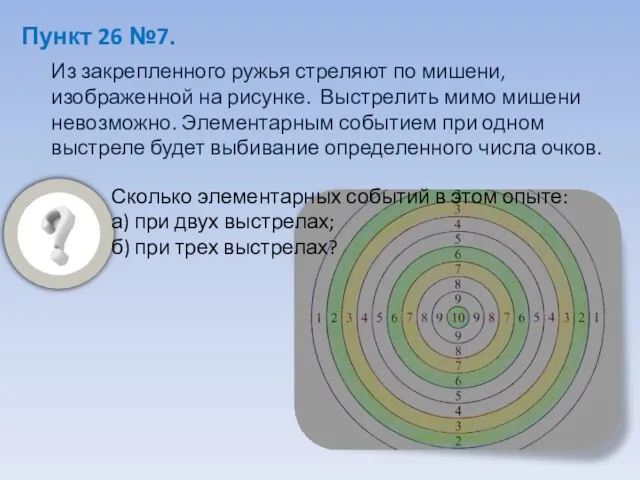
Пункт 26 №7.
Из закрепленного ружья стреляют по мишени, изображенной на рисунке. Выстрелить мимо мишени невозможно. Элементарным событием при одном выстреле будет выбивание определенного числа очков.
Сколько элементарных событий в этом опыте:
а) при двух выстрелах;
б) при трех выстрелах?

А) При двух выстрелах, элементарных событий 10х10=100, к каждому из десяти возможных элементарных событий при первом выстреле может присоединиться любое из десяти событий при втором выстреле. Все эти 100 элементарных событий записаны в таблице.
Б) При трёх выстрелах, элементарных событий 10х10х10=1000, к каждому из десяти возможных элементарных событий при первом выстреле может присоединиться любое из десяти событий при втором выстреле и может присоединиться любое из десяти событий при третьем выстреле.
а) При двух выстрелах 100 элементарных событий
б) При трёх выстрелах 1000 элементарных событий.

Пункт 26 №8. Спортивная команда «Математик» проводит товарищескую встречу по волейболу с командой «Физик». Ничья невозможна. Встреча проводится до двух побед одной из команд. Победу «Математика» обозначим буквой М, а победу «Физика»— буквой Ф. Одним из элементарных событий является ММ.
а) Запишите все возможные элементарные события.
б) Запишите все элементарные события, при которых встречу выигрывает команда «Физик».
Элементарные события :
ММ,ФФ,МФМ, ФММ, ФМФ,МФФ
ФФ,ФМФ,МФФ
Две буквы Ф, одна из которых является последней

Пункт 26 №8. Спортивная команда «Математик» проводит товарищескую встречу по волейболу с командой «Физик». Ничья невозможна. Встреча проводится до двух побед одной из команд. Победу «Математика» обозначим буквой М, а победу «Физика»— буквой Ф. Одним из элементарных событий является ММ.
в) Предположим, что во встрече победила команда «Математик». Какой буквой оканчивается запись соответствующих элементарных событий?
г) Какое наибольшее количество матчей может состояться?
Запись оканчивается буквой М
3 матча
Если после первых двух игр победитель не определился,
то победитель третьего матча станет победителем встречи

Пункт 26 №9. Красная Шапочка идет от домика мамы до домика бабушки. Красная Шапочка может идти только по дорожкам слева направо. Схема дорожек показана на рисунке. Каждая дорожка обозначена буквой. Например, один из возможных путей записывается как ах, другой — как bz. Перечислите все возможные пути Красной Шапочки в домик бабушки. Сколько получилось таких путей?

Пункт 26 №10. Красная Шапочка идет от домика мамы до домика бабушки. Красная Шапочка может идти только по дорожкам слева направо. Схема дорожек показана на рисунке. Каждая дорожка обозначена буквой. Сколько элементарных событий в этом опыте записывается одной, двумя, тремя буквами?
1) Одной буквой может быть записано 2 элементарных события: d и w.
2) Двумя буквами может быть записано 2 элементарных события: ax и bx.
3) Тремя буквами может быть записано 4 элементарных события: auw, buw, avw, bvw

Пункт 26 №11. Игральную кость подбрасывают трижды. Сколько элементарных событий в этом эксперименте?
У кости 6 граней, следовательно
количество элементарных событий равно
6·6·6=216

Пункт 26 №12. Игральную кость подбрасывают трижды. Найдите число элементарных событий, при которых в сумме выпало: а) 2 очка; б) З очка; в) 4 очка.
а) 0, т.к это невозможное событие.
б)1, при выпадении 111
в)3, при выпадении 112,121,211

Пункт 26 №13. Игральную кость подбрасывают трижды. Найдите число элементарных событий, при которых в сумме выпало более: а) 17 очков; б) 16 очков; в) 15 очков.
а) «выпало более17 очков»
элементарное событие: 6+6+6
Всего 1 элементарное событие.
б) «выпало более16 очков»
элементарные события: 5+6+6, 6+6+5, 6+5+6, 6+6+6.
Всего 4 элементарных события.
в) «выпало более15 очков».
элементарные события:
4+6+6, 6+6+4, 6+4+6,
5+5+6, 5+6+5, 6+5+5,
5+6+6, 6+5+6, 6+6+5,
6+6+6. Всего 10 элементарных событий.