Слайд 2Понятие степени
Степенью числа а с натуральным показателем n, большим единицы, называется произведение

n множителей, каждый из которых равен а.
35=3*3*3*3*3
Слайд 5Показатель и основание степени
(-2)4
Минус два-основание степени
Четыре-показатель степени

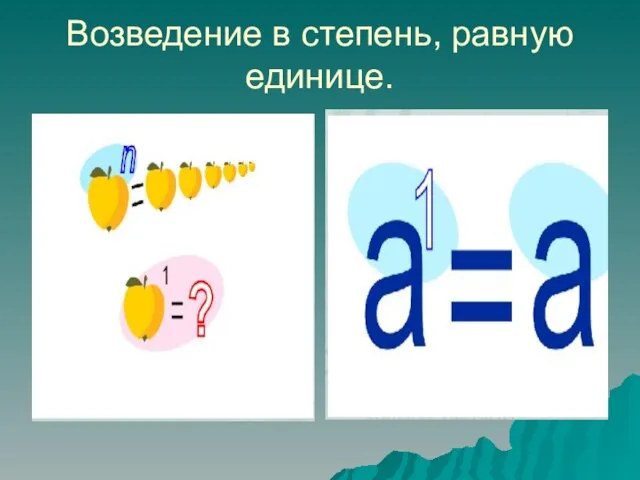
Слайд 6Возведение в степень, равную единице.
Слайд 7Степень с нулевым показателем.
70=1
(-25)0=1
(-2,6)0=1
20080=1

Слайд 8Нуль в нулевой степени
Любое число, кроме нуля, в нулевой степени равно единице.

Но нуль в нулевой степени не имеет смысла!
50=1
00=?
Слайд 9Возведение в степень отрицательных чисел.
(-2)4=
(-2)(-2)(-2)(-2)=16
(-2)3=(-2)(-2)(-2)=-8

Слайд 10Умножение и деление степеней
аm an=a m+n
Примеры:
а6 а11=а17
а9 а=а9 а1=а10
am :an=am-n
Примеры:
1.в9:в3=в6
в25:в24=в1=в

Слайд 11Нельзя складывать или вычитать степени!
53 + 54 ≠ 57
712 – 79

≠ 73
Слайд 12Возведение в степень произведения и степени.
(а n) m= a mn
(а 6)3= а

18
(в 5) 4=в20
(a b) n= an bn
(а в )7= а 7в7
(2в)2= 22в2=
=4в2













 Лицейская лирика Пушкина. Дружба и друзья в творчестве Пушкина
Лицейская лирика Пушкина. Дружба и друзья в творчестве Пушкина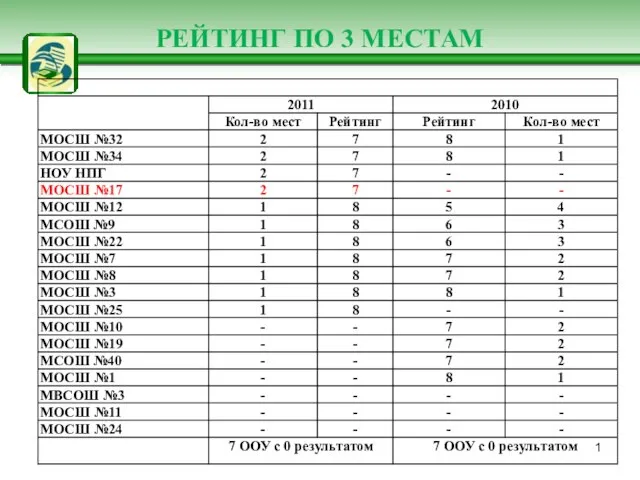 Рейтинг по 3 местам
Рейтинг по 3 местам Интерактивные методы обучения
Интерактивные методы обучения Презентация на тему Скелет строение и состав костей
Презентация на тему Скелет строение и состав костей Презентация на тему Консульство и образование наполеоновской империи
Презентация на тему Консульство и образование наполеоновской империи  Операторство. Кто такой кинооператор?
Операторство. Кто такой кинооператор? Проект вариативной части Учебного плана АМОУ СОШ №8 на 2011-2012 учебный год
Проект вариативной части Учебного плана АМОУ СОШ №8 на 2011-2012 учебный год ACUTE CHOLECYSTITIS
ACUTE CHOLECYSTITIS  Физиология высшей нервной деятельности
Физиология высшей нервной деятельности Великая Отечественная война в жизни нашей семьи
Великая Отечественная война в жизни нашей семьи Музей-усадьба Льва Толстого
Музей-усадьба Льва Толстого Индуктивные преобразователи
Индуктивные преобразователи ÐÑезенÑаÑиÑ1
ÐÑезенÑаÑиÑ1 Формирование учебной мотивации у младших школьников
Формирование учебной мотивации у младших школьников ОТ БУКВЫ – К СМЫСЛУ СЛОВА
ОТ БУКВЫ – К СМЫСЛУ СЛОВА Эффективные управленческие технологии в деятельности руководителя образовательного учреждения
Эффективные управленческие технологии в деятельности руководителя образовательного учреждения Этические нормы разработки сайтов. Возможность формирования кодекса этических норм веб-разработчиков
Этические нормы разработки сайтов. Возможность формирования кодекса этических норм веб-разработчиков Цвет в произведения живописи
Цвет в произведения живописи Регулируемый навес для нижней базы
Регулируемый навес для нижней базы КОНСТИТУЦИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КОНСТИТУЦИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Какие бывают государства
Какие бывают государства Массивы
Массивы Источники питания для сварки
Источники питания для сварки Какой бывает транспорт? 2 класс
Какой бывает транспорт? 2 класс Презентация на тему Заболевание рахит
Презентация на тему Заболевание рахит Золотое правило нравственности (4 класс)
Золотое правило нравственности (4 класс) Презентация на тему Чудесные превращения воды в природе
Презентация на тему Чудесные превращения воды в природе Грамоты. Шаблон
Грамоты. Шаблон