Математика

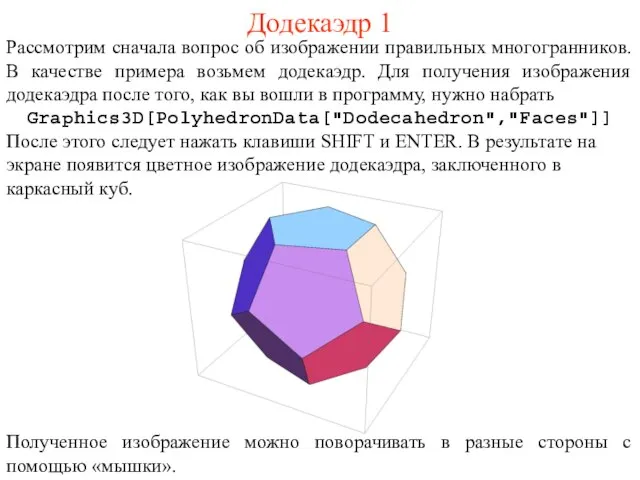
Рассмотрим сначала вопрос об изображении правильных многогранников. В качестве примера возьмем додекаэдр. Для получения изображения додекаэдра после того, как вы вошли в программу, нужно набрать
Graphics3D[PolyhedronData["Dodecahedron","Faces"]]
После этого следует нажать клавиши SHIFT и ENTER. В результате на экране появится цветное изображение додекаэдра, заключенного в каркасный куб.
Додекаэдр 1
Полученное изображение можно поворачивать в разные стороны с помощью «мышки».

Додекаэдр 2
Если вы хотите убрать куб, то к команде, которую вы набрали, следует добавить Boxed->False. В результате получится команда
Graphics3D[PolyhedronData["Dodecahedron","Faces"],Boxed->False]
Нажатие клавиш SHIFT и ENTER приводит к исполнению этой команды. На экране получим изображение додекаэдра

Додекаэдр 3
Изображение додекаэдра можно сделать разной степени прозрачным. Для этого нужно добавить команду Opacity[k], где k – коэффициент прозрачности от нуля до единицы. Если k=1, то прозрачности нет. Если k=0, то от изображения додекаэдра остаются только ребра. На рисунке приведена команда и изображение в случае k=0,8.
Graphics3D[{Opacity[0.8],PolyhedronData["Dodecahedron","Faces"]},Boxed->False]

Додекаэдр 4
Цвет граней додекаэдра можно изменить, добавив команду FaceForm[], где в квадратных скобках указывается цвет. Если выбрать желтый цвет (Yellow), то получим команду
Graphics3D[{Opacity[0.8],FaceForm[Yellow],PolyhedronData["Dodecahedron","Faces"]},Boxed®False]
Исполнение которой дает следующее изображение.

Додекаэдр 5
Изображение ребер додекаэдра можно делать разного цвета и разной толщины. Пример дает следующая команда
Graphics3D[{EdgeForm[{GrayLevel[0.5],Thickness[0.02]}],PolyhedronData["Dodecahedron","Faces"]}]

Додекаэдр 6
Следующая команда позволяет получить изображение развертки додекаэдра.
PolyhedronData["Dodecahedron","NetImage"]

Додекаэдр 7
Программа «Математика» позволяет вычислять значения различных геометрических величин, связанных с многогранниками.
Например, команда
PolyhedronData["Dodecahedron","Circumradius"]
дает радиус сферы, описанной около додекаэдра с ребром 1,
Команда
PolyhedronData["Dodecahedron","Inradius"]
дает радиус сферы, вписанной в додекаэдр с ребром 1,

Додекаэдр 8
Команда
PolyhedronData["Dodecahedron","Volume"]
Дает объем додекаэдра с ребром 1,
Команда
PolyhedronData["Dodecahedron","SurfaceArea"]
Дает площадь поверхности додекаэдра с ребром 1,

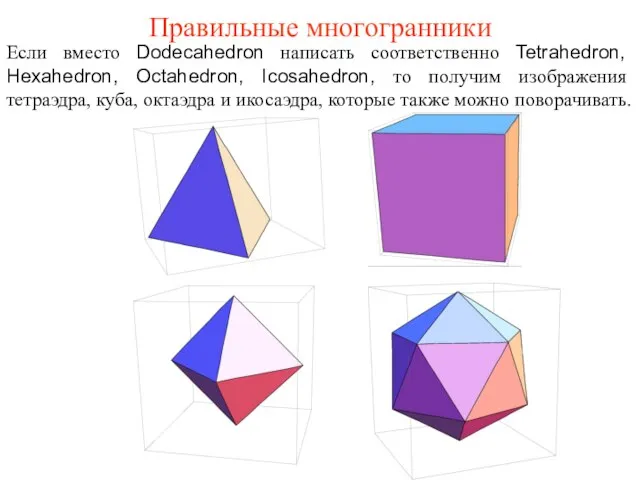
Правильные многогранники
Если вместо Dodecahedron написать соответственно Tetrahedron, Hexahedron, Octahedron, Icosahedron, то получим изображения тетраэдра, куба, октаэдра и икосаэдра, которые также можно поворачивать.

Полуправильные многогранники
Программа «Математика 7» позволяет получать изображения полуправильных многогранников и производить с ними указанные выше операции. Среди них: правильные призмы и антипризмы.
На рисунках приведены правильная шестиугольная призма и пятиугольная антипризма, полученные с помощью команд соответственно:
PolyhedronData[{"Prism",6}]) PolyhedronData[{"Antiprism",5}])

Тела Архимеда
1. Усеченный тетраэдр
(команда PolyhedronData["TruncatedTetrahedron"])
Кроме правильных призм и антипризм к полуправильным многогранникам относятся 13 тел Архимеда. Среди них.

2. Усеченный куб
(команда PolyhedronData["TruncatedCube"])

3. Усеченный октаэдр
(команда PolyhedronData["TruncatedOctahedron"])

4. Усеченный икосаэдр
(команда PolyhedronData["TruncatedIcosahedron"])

5. Усеченный додекаэдр
(команда PolyhedronData["TruncatedDodecahedron"])

6. Кубооктаэдр
(команда PolyhedronData["Cuboctahedron"])

7. Икосододекаэдр
(команда PolyhedronData["Icosidodecahedron"])

8. Усеченный кубооктаэдр
(команда PolyhedronData["GreatRhombicuboctahedron"]).

9. Усеченный икосододекаэдр
(команда PolyhedronData["GreatRhombicosidodecahedron"])

10. Ромбокубооктаэдр
(команда PolyhedronData["SmallRhombicuboctahedron"])

11. Ромбоикосододекаэдр
(команда PolyhedronData["SmallRhombicosidodecahedron"])

12. Курносый куб
(команда PolyhedronData["SnubCube"])

13. Курносый додекаэдр
(команда PolyhedronData["SnubDodecahedron"])

Правильные звездчатые многограннники
Программа «Математика 7» позволяет получать изображения правильных звездчатых многогранников (тел Кеплера-Пуансо) и производить с ними указанные выше операции.
Имеется четыре правильных звездчатых многогранников:
1. Малый звездчатый додекаэдр (команда PolyhedronData["SmallStellatedDodecahedron"]).

2. Большой звездчатый додекаэдр
(команда PolyhedronData["GreatStellatedDodecahedron"])

3. Большой додекаэдр
(команда PolyhedronData["GreatDodecahedron"])

4. Большой икосаэдр
(команда PolyhedronData["GreatIcosahedron"])

Список групп многогранников
В программе «Математика 7» имеется много других многогранников, объединенных в группы. Названия этих групп можно получить с помощью команды
PolyhedronData["Classes"]
Ее исполнение дает следующий список групп.
{Amphichiral,Antiprism,Archimedean,ArchimedeanDual,Chiral,Compound,Concave,Convex,Cuboid,Deltahedron,Dipyramid,Equilateral,Hypercube,Johnson,KeplerPoinsot,Orthotope,Platonic,Prism,Pyramid,Quasiregular,RectangularParallelepiped,Rhombohedron,Rigid,SelfDual,Shaky,Simplex,SpaceFilling,Stellation,Uniform,UniformDual,Zonohedron}

Группа “Compound”
Для получения названий многогранников, входящих, например, в группу Compound нужно набрать команду
PolyhedronData["Compound"]
Ее исполнение дает следующий список названий многогранников.
{CubeFiveCompound,CubeFourCompound,CubeOctahedronCompound,CubeOctahedronFiveCompound,CubeOctahedronThreeCompound,CubeSixCompound,CubeTenCompound,CubeThreeCompound,CubeTwoCompound,DodecahedronFiveCompound,DodecahedronIcosahedronCompound,DodecahedronSixCompound,DodecahedronTwoCompound,HexagonalPrismSixCompound,IcosahedronFiveCompound,IcosahedronSixCompound,IcosahedronTwoCompound,OctahedronFiveCompound,OctahedronFourCompound,OctahedronTenCompound,OctahedronThreeCompound,StellaOctangula,TetrahedronFiveCompound,{TetrahedronFourCompound,1},{TetrahedronFourCompound,2},{TetrahedronFourCompound,3},TetrahedronSixCompound,TetrahedronTenCompound,TetrahedronThreeCompound,TetrahedronTwoCompound}

Соединение пяти тетраэдров
Если, например, набрать команду
PolyhedronData["TetrahedronFiveCompound"]
то ее исполнение даст изображение соединения из пяти тетраэдров.

Группа “Stellation”
Для получения названий многогранников, входящих, например, в группу Stellation нужно набрать команду
PolyhedronData["Stellation"]
Ее исполнение дает следующий список названий многогранников.
{CubeFiveCompound,DodecahedronIcosahedronCompound,Echidnahedron,EschersSolid,GreatDodecahedron,GreatIcosahedron,GreatRhombicTriacontahedron,GreatStellatedDodecahedron,OctahedronFiveCompound,{RhombicDodecahedronStellation,2},RhombicHexecontahedron,SmallStellatedDodecahedron,SmallTriambicIcosahedron,StellaOctangula,TetrahedronFiveCompound,TetrahedronTenCompound}