Математика в изобразительном искусстве

Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.

Голландский художник М.К. Эшер (1898-1972) в некотором роде является отцом математического искусства. Математические идеи играют центральную роль в большинстве его картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдохновения для современных авторов.

МНОГОГРАННИКИ
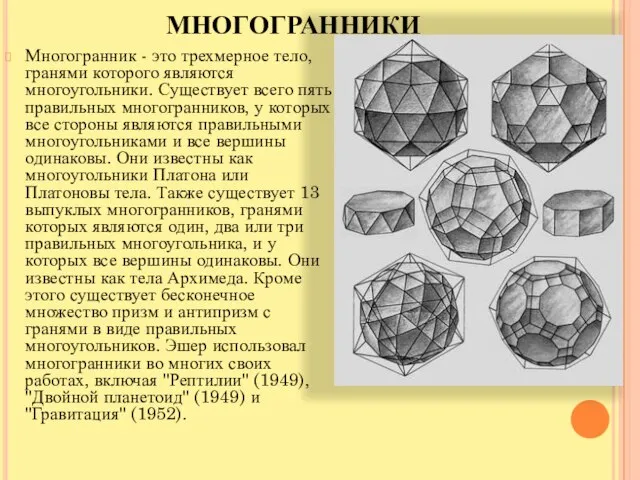
Многогранник - это трехмерное тело, гранями которого являются многоугольники. Существует всего пять правильных многогранников, у которых все стороны являются правильными многоугольниками и все вершины одинаковы. Они известны как многоугольники Платона или Платоновы тела. Также существует 13 выпуклых многогранников, гранями которых являются один, два или три правильных многоугольника, и у которых все вершины одинаковы. Они известны как тела Архимеда. Кроме этого существует бесконечное множество призм и антипризм с гранями в виде правильных многоугольников. Эшер использовал многогранники во многих своих работах, включая "Рептилии" (1949), "Двойной планетоид" (1949) и "Гравитация" (1952).

ТЕССЕЛЛЯЦИИ
Тесселляции, известные также как покрытие плоскости плитками, являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций.Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968). Примеры ниже - картины современных авторов Холлистера Девида и Роберта Фатауэра.

HOLLISTER DAVID "СЕМЬ ПТИЦ". НА ЭТОЙ КАРТИНЕ ИЗОБРАЖЕНЫ СЕМЬ ПТИЦ, ДВЕ ИЗ КОТОРЫХ ИЗОБРАЖЕНЫ В НЕГАТИВЕ НА ФОНЕ ЛАНДШАФТА ГОРОДА АХО В АРИЗОНЕ. ПОСЛЕДОВАТЕЛЬНО УМЕНЬШАЮЩИЕСЯ ФИГУРЫ ПТИЦ СОВМЕЩАЮТСЯ ДРУГ С ДРУГОМ В ВИДЕ ФРАКТАЛЬНОЙ ТЕССЕЛЛЯЦИИ. ХВОСТОВЫЕ ПЕРЬЯ КАЖДОЙ ПТИЦЫ ЯВЛЯЮТСЯ РАЗДЕЛЯЮТ КОНСТРУКЦИЮ НАПОПОЛАМ, ОТСЕКАЯ ПРИМЕРНО ТРЕТЬ РАССТОЯНИЯ МЕЖДУ КОНЧИКАМИ КРЫЛЬЕВ. КАЖДАЯ МЕНЬШАЯ ПТИЦА В СВОЮ ОЧЕРЕДЬ ДЕЛИТ СВОЮ ОБЛАСТЬ АНАЛОГИЧНЫМ ОБРАЗОМ. ЕСЛИ ЭТОТ ПРОЦЕСС ПРОДОЛЖАТЬ ДО БЕСКОНЕЧНОСТИ, ПОЛУЧИТСЯ НАБОР ТОЧЕК, ИЗВЕСТНЫЙ КАК МНОЖЕСТВО КАНТОРА ИЛИ КАНТОРОВА ПЫЛЬ.

ROBERT FATHAUER "ФРАКТАЛЬНЫЕ РЫБЫ - СГРУППИРОВАННЫЕ ГРУППЫ". ЭТО КОМПЬЮТЕРНАЯ РАБОТА, РАСПЕЧАТАННАЯ НА ФОТОБУМАГЕ. СКВОЗЬ ИЛЛЮМИНАТОР ВИДНЫ ВОЛНЫ, НО ПРИ БЛИЖАЙШЕМ РАССМОТРЕНИИ ВИДНО, ЧТО ВОЛНЫ ЯВЛЯЮТСЯ НА САМОМ ДЕЛЕ ФРАКТАЛЬНОЙ ТЕССЕЛЛЯЦИЕЙ, СОСТОЯЩЕЙ ИЗ РЫБ.

ИСКАЖЕННЫЕ И НЕОБЫЧНЫЕ ПЕРСПЕКТИВЫ
Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство.
Dick Termes
"Клетка для человека"
(1978)

НЕВОЗМОЖНЫЕ ФИГУРЫ
Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер"Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск"Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск" (1960) и "Водопад" (1961). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана Ороса

ЛЕНТА МЕБИУСА
Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один концов полоски, а затем склеив оба конца друг с другом. Эшер изобразил ленту Мебиуса на работах "Всадники" (1946), "Лента Мебиуса II (Красные муравьи)" (1963) и "Узлы" (1965).

ФРАКТАЛЫ
Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей. К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Он использовал сжимающиеся координатные сетки и гиперболическую геометрию для достижения этого эффекта, как показано в картинах "Предел круга" I-IV (1958-1960) и "Предел квадрата" (1964). Ниже приведены примеры современных художников Кэри Митчелл и Роберта Фатауэра.

KERRY MITCHELL "БУДДА" - КОМПЬЮТЕРНАЯ КАРТИНА ОСНОВАННАЯ НА МНОЖЕСТВЕ МАНДЕЛЬБРОТА, ИССЛЕДОВАННОГО БЕНУА МАНДЕЛЬБРОТОМ

ROBERT FATHAUER "КОМПОЗИЦИЯ КРУГОВ" (2001) - НЕ ЯВЛЯЕТСЯ ВЫЧИСЛЯЕМЫМ ФРАКТАЛОМ, ОДНАКО МОЖЕТ БЫТЬ ПОЛУЧЕН ГРАФИЧЕСКИ, УПАКОВЫВАЯ МЕНЬШИЕ КРУГИ В БОЛЬШИХ.

СВЯЗЬ МАТЕМАТИКИ И ИЗОБРАЗИТЕЛЬНОГО ИСКУССТВА ПРИ КОНСТРУКТИВНОМ ПОСТРОЕНИИ НАТЮРМОРТА.
Натюрморт (фр. nature morte — букв. «мертвая природа») — изображение неодушевлённых предметов в изобразительном искусстве, в отличие от портретной, жанровой, исторической и пейзажной тематики.
При построении натюрморта используются такие понятия как: параллельные прямые, геометрические фигуры, отношения, пропорции, оси симметрии. Приведём пример построения на простейшем натюрморте, состоящем из трёх предметов(ваза, кружка, груша)

Ваза
При построении в первую очередь учитывается отношение высоты вазы к ширине. h/b
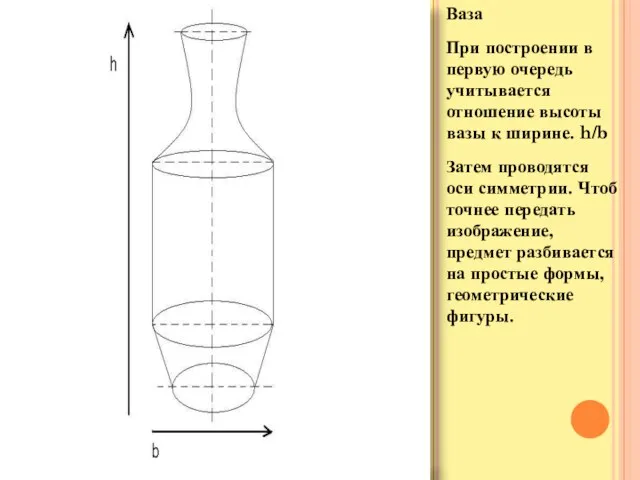
Затем проводятся оси симметрии. Чтоб точнее передать изображение, предмет разбивается на простые формы, геометрические фигуры.

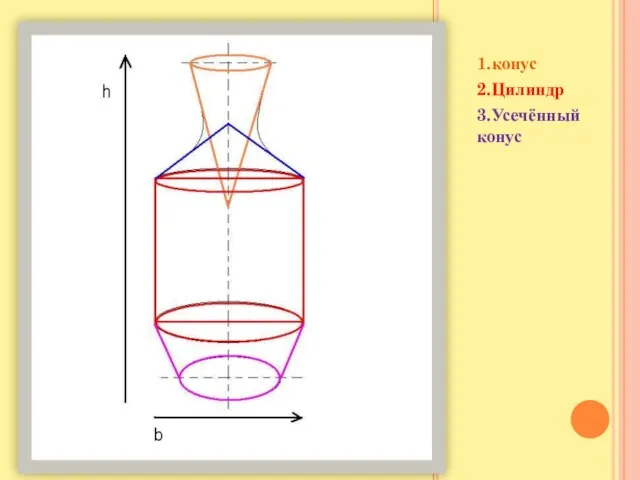
1.конус
2.Цилиндр
3.Усечённый конус

То же самое проделывается и в отношении кружки и груши. Оси симметрии, отношение высоты к ширине, разбивание предметов на простые формы.

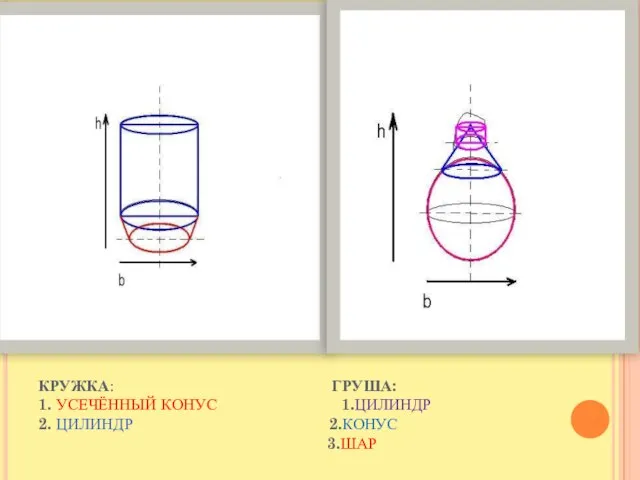
КРУЖКА: ГРУША:
1. УСЕЧЁННЫЙ КОНУС 1.ЦИЛИНДР
2. ЦИЛИНДР 2.КОНУС
3.ШАР

Соединяем три элемента . При этом мы должны учитывать
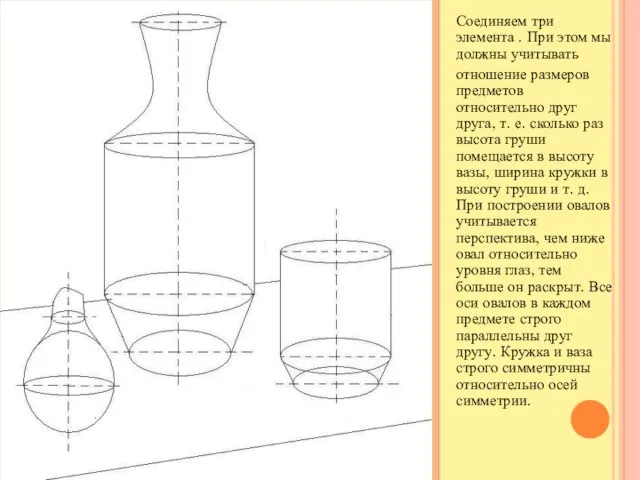
отношение размеров предметов относительно друг друга, т. е. сколько раз высота груши помещается в высоту вазы, ширина кружки в высоту груши и т. д. При построении овалов учитывается перспектива, чем ниже овал относительно уровня глаз, тем больше он раскрыт. Все оси овалов в каждом предмете строго параллельны друг другу. Кружка и ваза строго симметричны относительно осей симметрии.