Содержание
- 2. Проклятие размерности Ричард Эрнест Бе́ллман (26 августа 1920, Нью-Йорк, США — 19 марта 1984, Лос-Анджелес, США)
- 3. Пример проклятия размерности Рассмотрим единичный интервал [0,1]. 100 равномерно разбросанных точек будет достаточно, чтобы покрыть этот
- 4. Сферы возникновения Машинное обучение Задачи распознавания Задачи оптимизации Комбинаторная геометрия Работа со сложными системами
- 5. Трудности при работе со сложными системами Трудоемкость вычислений Необходимость хранения огромного количества данных Увеличение доли шумов
- 6. Способ решения Основная идея при решении проблемы — понизить размерность пространства, а именно спроецировать данные на
- 7. Пример проецирования данных на подпространство меньшей размерности
- 8. История появления Гарольд Хотеллинг (29 сентября 1895, Фулда, Миннесота — 26 декабря 1973, Чапел-Хилл, Северная Каролина)
- 9. Эквивалентные постановки метода главных компонент 1. Аппроксимировать данные линейными многообразиями меньшей размерности 2. Найти подпространства меньшей
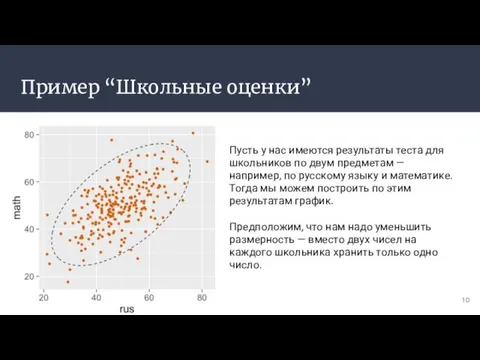
- 10. Пример “Школьные оценки” Пусть у нас имеются результаты теста для школьников по двум предметам — например,
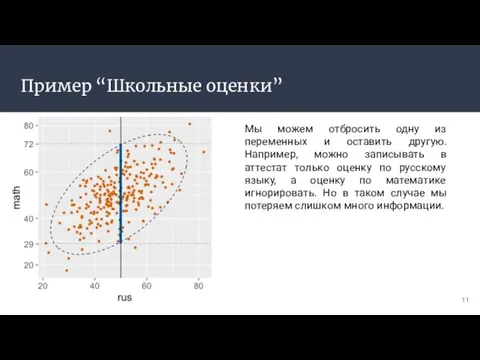
- 11. Пример “Школьные оценки” Мы можем отбросить одну из переменных и оставить другую. Например, можно записывать в
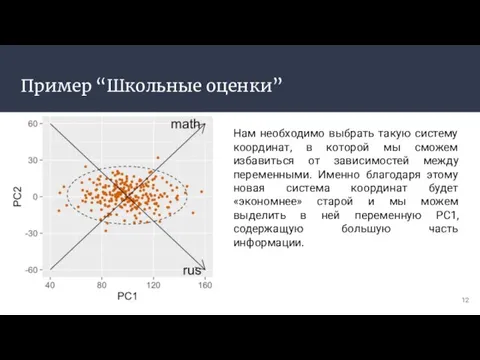
- 12. Пример “Школьные оценки” Нам необходимо выбрать такую систему координат, в которой мы сможем избавиться от зависимостей
- 13. Основные понятия Линейное многообразие M = {v + x | x ∈ L} Линейная комбинация Ортонормированная
- 14. Аппроксимация данных линейными многообразиями Дано: ?1, ?2, … , ?m ∈ ?n, ? = 1, 2,
- 15. Аппроксимация данных линейными многообразиями Решение задачи аппроксимации для ? = 1, 2, … , ? –
- 16. Аппроксимация данных линейными многообразиями Ищем такой вектор, при котором максимизировалась бы дисперсия проекции нашей выборки на
- 17. Диагонализация ковариационной матрицы Векторы главных компонент для задач о наилучшей аппроксимации и о поиске ортогональных проекций
- 18. Диагонализация ковариационной матрицы Если спектр ковариационной матрицы вырожден, то выбирают произвольный ортонормированный базис собственных векторов. Он
- 19. Подавление шума на изображениях
- 20. Примеры Биоинформатика Хемометрика Индексация видео Общественные науки
- 21. Применение для визуализации Проекция ДНК-блуждания на первые 2 главные компоненты для генома бактерии «Streptomyces coelicolor».
- 23. Скачать презентацию

![Пример проклятия размерности Рассмотрим единичный интервал [0,1]. 100 равномерно разбросанных точек будет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/906733/slide-2.jpg)















 Международное сотрудничество в области сертификации. Схемы сертификации. Добровольная и обязательная сертификация. Сделали: Тор
Международное сотрудничество в области сертификации. Схемы сертификации. Добровольная и обязательная сертификация. Сделали: Тор Международный день без интернета
Международный день без интернета Разделенный город как крайняя форма сегрегации городского пространства
Разделенный город как крайняя форма сегрегации городского пространства Японский виски
Японский виски Тема урока: «Прямоугольник и квадрат»
Тема урока: «Прямоугольник и квадрат» Гражданское общество и правовое государство
Гражданское общество и правовое государство Эллинистические государства в IV-IIв. до н.э. Эллинистическая культура
Эллинистические государства в IV-IIв. до н.э. Эллинистическая культура Hungry Frog
Hungry Frog Анонимные Наркоманы
Анонимные Наркоманы ТЕМА УРОКА:
ТЕМА УРОКА: Русский язык
Русский язык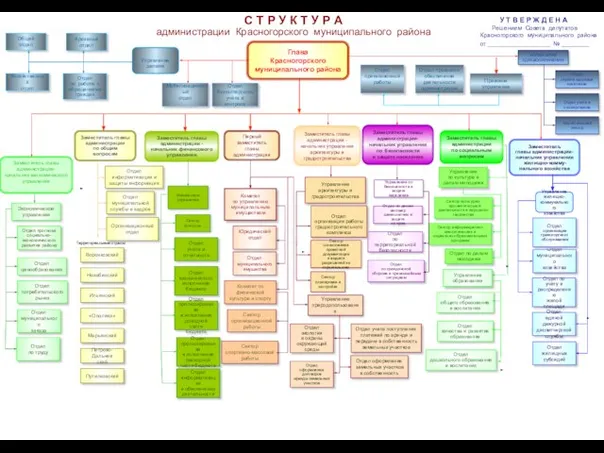 С Т Р У К Т У Р А администрации Красногорского муниципального района
С Т Р У К Т У Р А администрации Красногорского муниципального района Презентация на тему Историко-культурные объекты, сформированные на территории средневекового Тараза Южного Казахстана
Презентация на тему Историко-культурные объекты, сформированные на территории средневекового Тараза Южного Казахстана Финансовая математика
Финансовая математика Реновация промышленных зданий
Реновация промышленных зданий Как менялась этика на протяжении веков
Как менялась этика на протяжении веков Классный час «Жизнь – это…»
Классный час «Жизнь – это…» Sale 30% Bestia
Sale 30% Bestia Presentation Title
Presentation Title  Продажа мобильного ПО своими руками
Продажа мобильного ПО своими руками Государственная (итоговая) аттестация выпускников 9-х классов
Государственная (итоговая) аттестация выпускников 9-х классов география
география Зеленый Меморандум СБ. Кейс 2
Зеленый Меморандум СБ. Кейс 2 Крещенские вечера
Крещенские вечера Институты и субинституты финансового права
Институты и субинституты финансового права Презентацию подготовил ученик 3 «А» класса ГОУ средней общеобразовательной школы № 511 Добролюбов Егор Учитель: Ваниосова Н.В.
Презентацию подготовил ученик 3 «А» класса ГОУ средней общеобразовательной школы № 511 Добролюбов Егор Учитель: Ваниосова Н.В. Приметы и суеверия. Les superstitions et les présages
Приметы и суеверия. Les superstitions et les présages Способы завязывания платков
Способы завязывания платков