Содержание
- 2. Статика – инженерная наука, изучающая равновесие твердых тел, находящихся под действием сил. Она необходима для определения
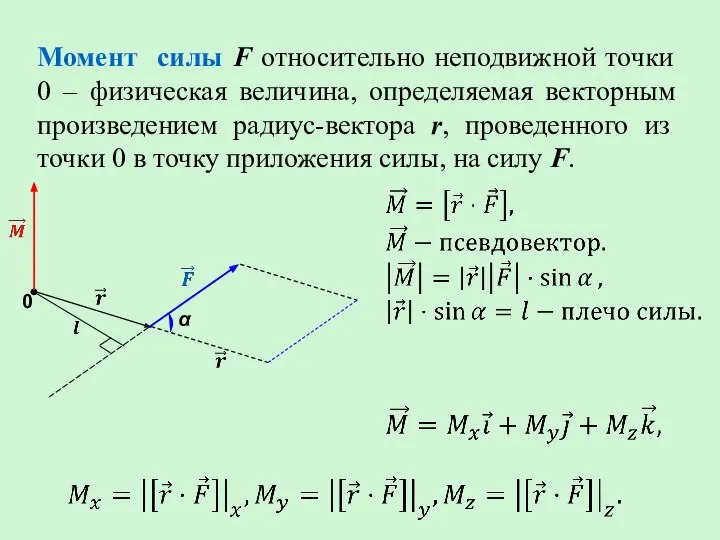
- 3. Момент силы F относительно неподвижной точки 0 – физическая величина, определяемая векторным произведением радиус-вектора r, проведенного
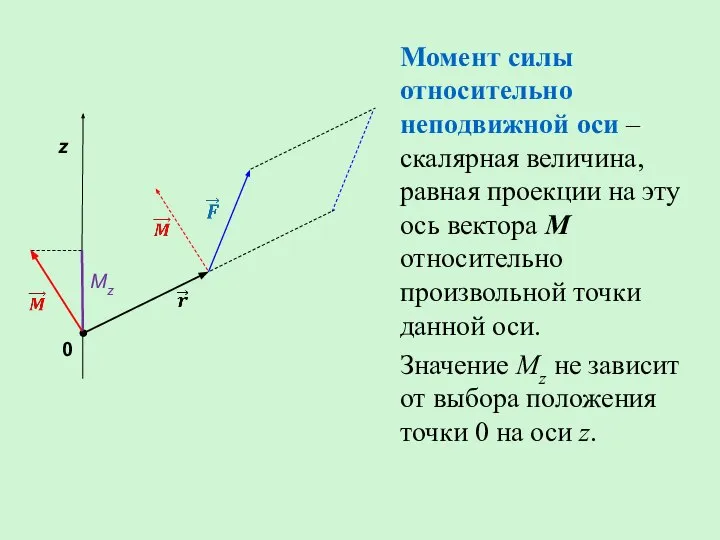
- 4. Момент силы относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора М относительно
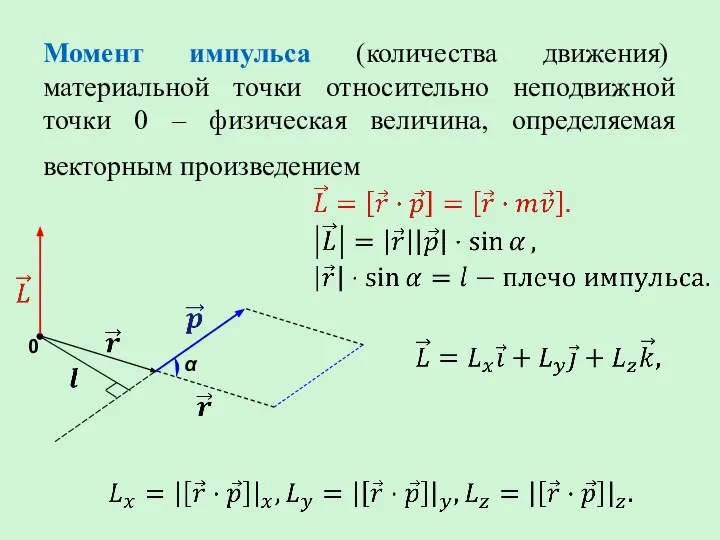
- 5. Момент импульса (количества движения) материальной точки относительно неподвижной точки 0 – физическая величина, определяемая векторным произведением
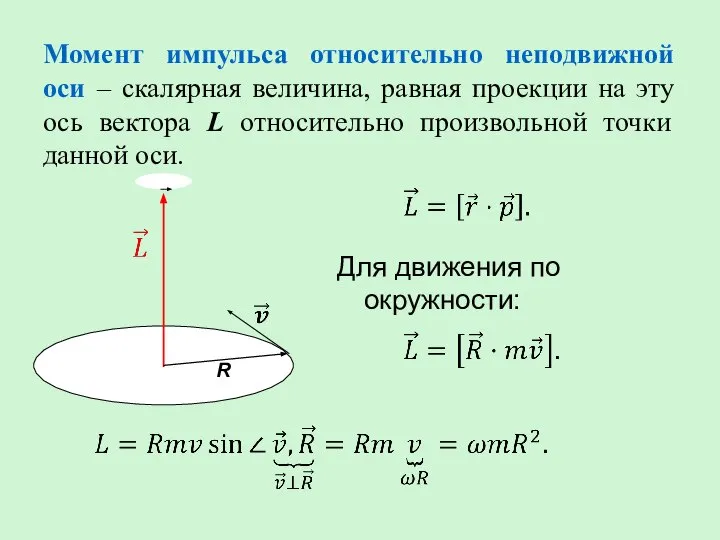
- 6. Момент импульса относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора L относительно
- 7. Уравнение моментов Математическая справка:
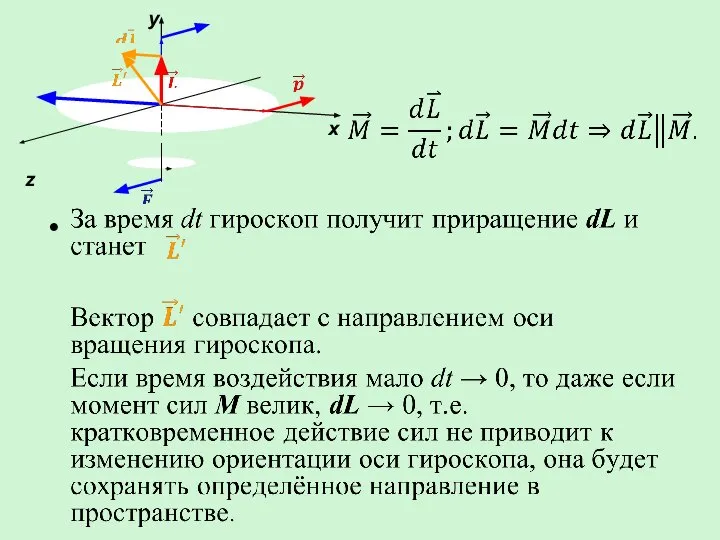
- 8. Производная по времени от момента импульса относительно точки равна моменту силы относительно этой точки. Производная по
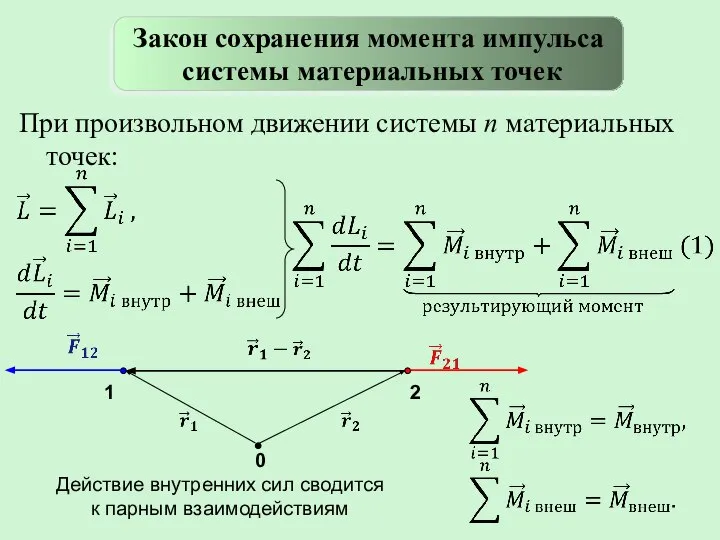
- 9. При произвольном движении системы n материальных точек: Закон сохранения момента импульса системы материальных точек Действие внутренних
- 10. Результирующий момент внутренних сил в соответствии с третьим законом Ньютона равен нулю.
- 12. Закон сохранения момента импульса является прямым следствием законов Ньютона и изотропности пространства – эквивалентности свойств пространства
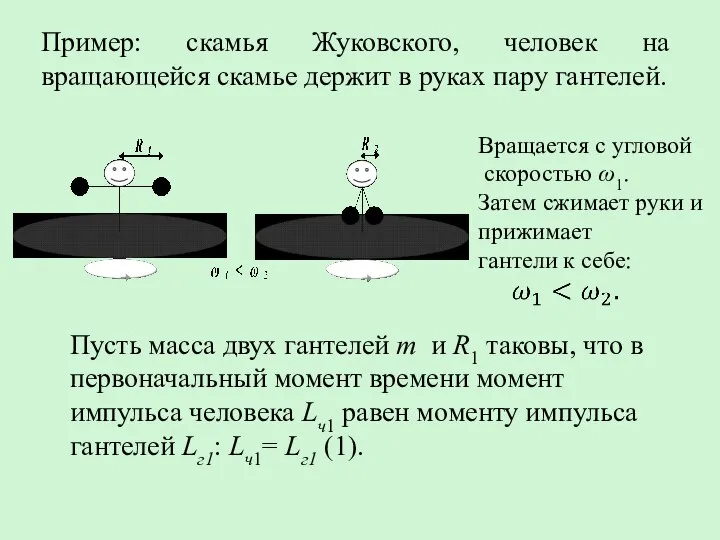
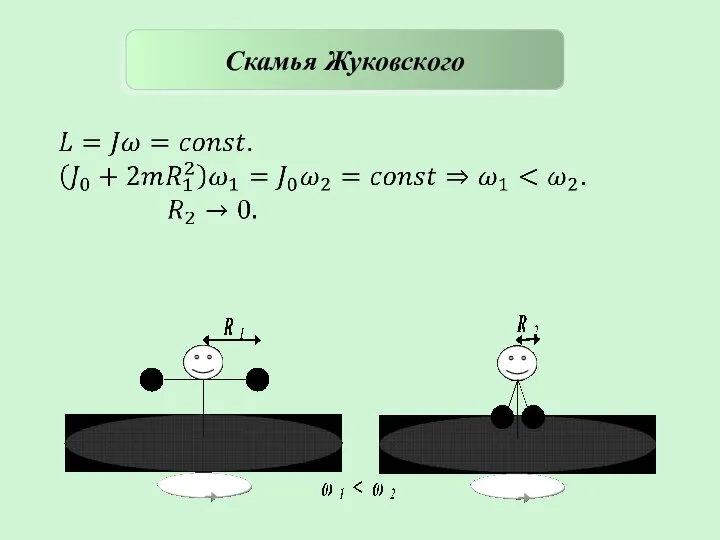
- 13. Пример: скамья Жуковского, человек на вращающейся скамье держит в руках пару гантелей. Пусть масса двух гантелей
- 14. Начальный момент импульса системы: Т.к. Lч1= Lг1
- 15. Уравнение (7) делим на (8): Уравнение (9) подставляем в (6): Уравнение (4) подставляем в (10):
- 16. Аналогичная ситуация возникает, когда фигурист прижимает руки к себе и начинает вращаться быстрее.
- 17. Гироскоп – быстро вращающееся симметричное твердое тело, ось вращения которого может изменять свое направление в пространстве.
- 18. Свойства гироскопа проявляются у вращающихся небесных тел, снаряда (пули), роторов турбин, установленных на судах, волчка, юлы.
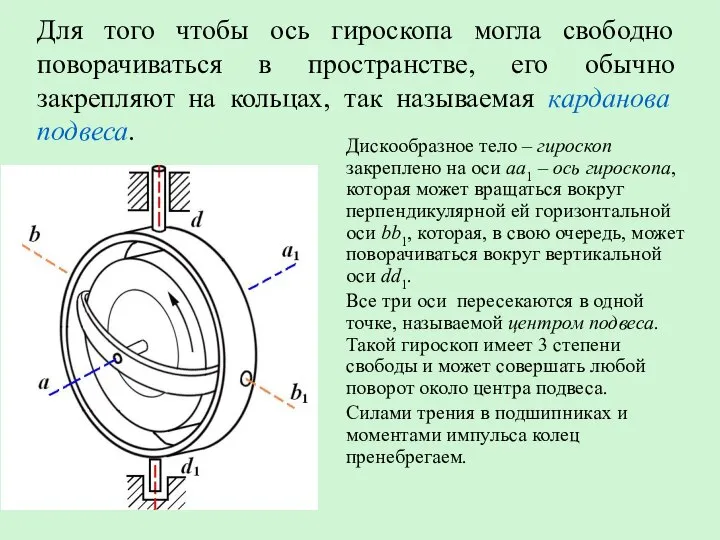
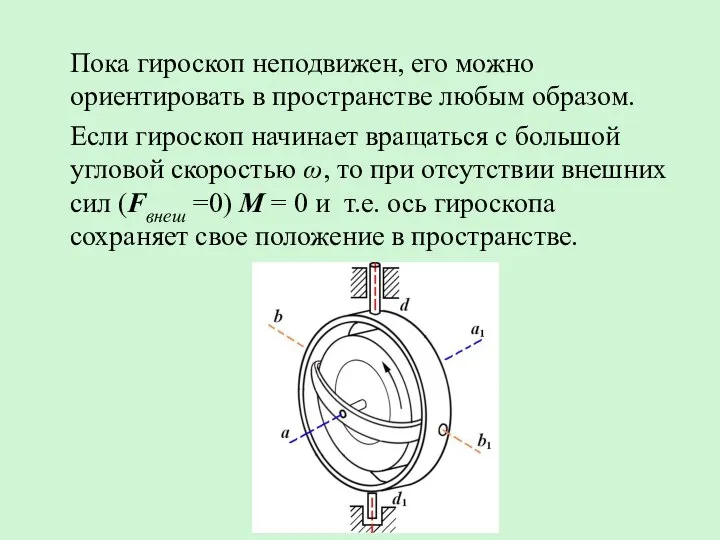
- 19. Для того чтобы ось гироскопа могла свободно поворачиваться в пространстве, его обычно закрепляют на кольцах, так
- 20. Пока гироскоп неподвижен, его можно ориентировать в пространстве любым образом. Если гироскоп начинает вращаться с большой
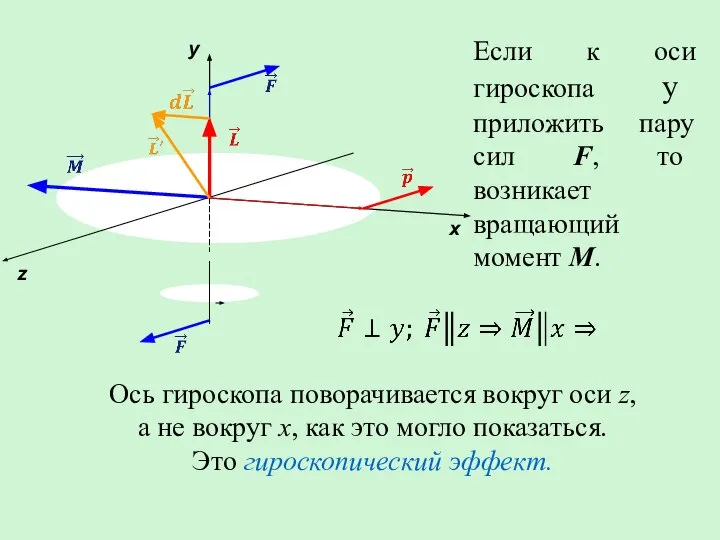
- 21. Если к оси гироскопа y приложить пару сил F, то возникает вращающий момент М. Ось гироскопа
- 23. Гироскоп Применение: - навигационные устройства (гирокомпас, гирогоризонт), - поддержание заданного направления движения (автопилот). При конструировании судов
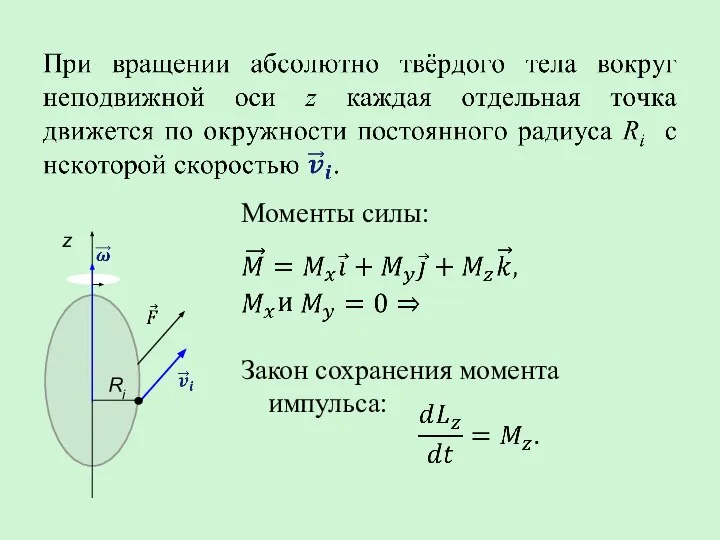
- 24. Динамика вращательного движения абсолютно твёрдого тела относительно неподвижной оси. Основное уравнение динамики вращательного движения
- 25. Моменты силы: Закон сохранения момента импульса:
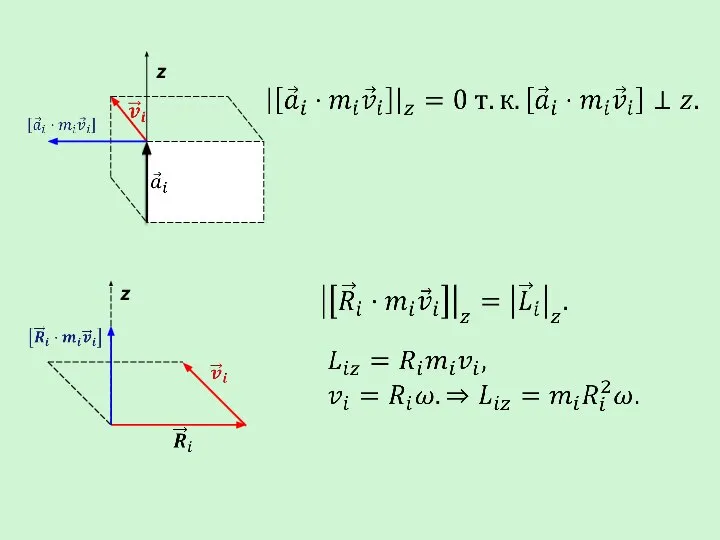
- 26. Момент импульса относительно точки 0 для i точки твёрдого тела: Проекция на ось z относительно точки
- 28. Твёрдое тело – система жёстко связанных материальных точек.
- 29. Закон сохранения момента импульса: Т.к. координатную ось z приняли произвольно, индекс можно опустить. – основное уравнение
- 30. В общем случае: – ускорение вращения твердого тела относительно неподвижной оси прямо пропорционально моменту всех внешних
- 31. Момент инерции. Теорема Гюйгенса-Штейнера
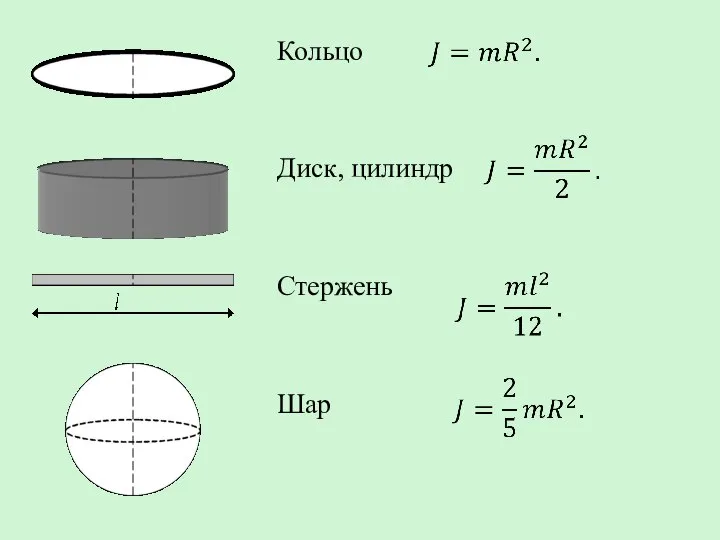
- 32. Кольцо Диск, цилиндр Стержень Шар
- 33. Теорема Гюйгенса-Штейнера: момент инерции относительно произвольной оси равен моменту инерции относительно параллельной ей оси, проходящей через
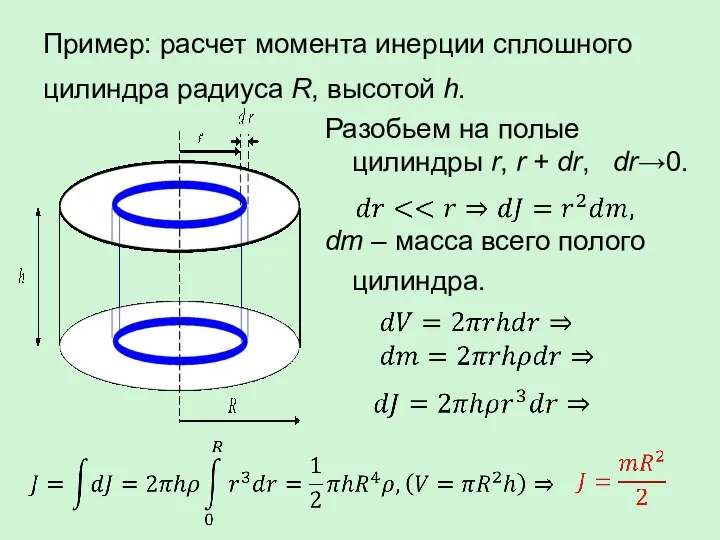
- 34. Пример: расчет момента инерции сплошного цилиндра радиуса R, высотой h. Разобьем на полые цилиндры r, r
- 35. Закон сохранения момента импульса АТТ относительно неподвижной оси
- 36. Скамья Жуковского
- 37. Т.к. имеется АТТ, следовательно, для всех mi ω = const. Кинетическая энергия при вращательном движении АТТ
- 38. Основное уравнение динамики вращательного движения: Закон сохранения момента импульса: Кинетическая энергия при вращательном движении: Работа и
- 39. Работа при вращательном движении идёт на увеличение его кинетической энергии:
- 40. Мощность:
- 41. Плоское движение – движение, при котором все участки траектории любых двух точек твёрдого тела лежат в
- 43. Скачать презентацию







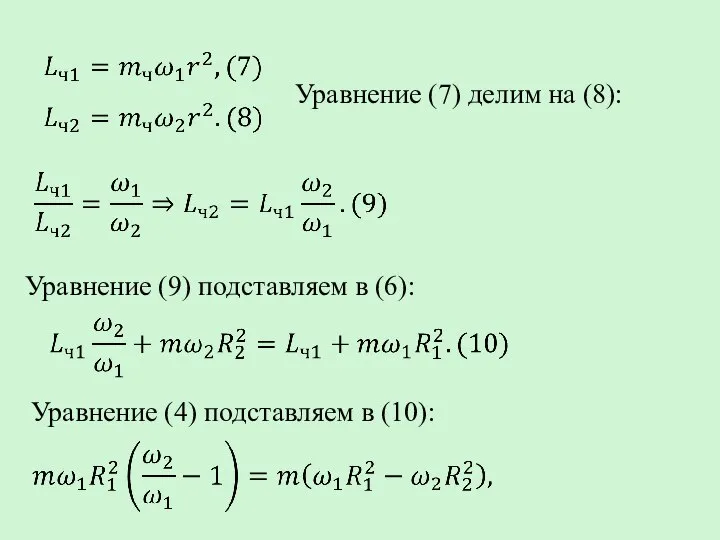















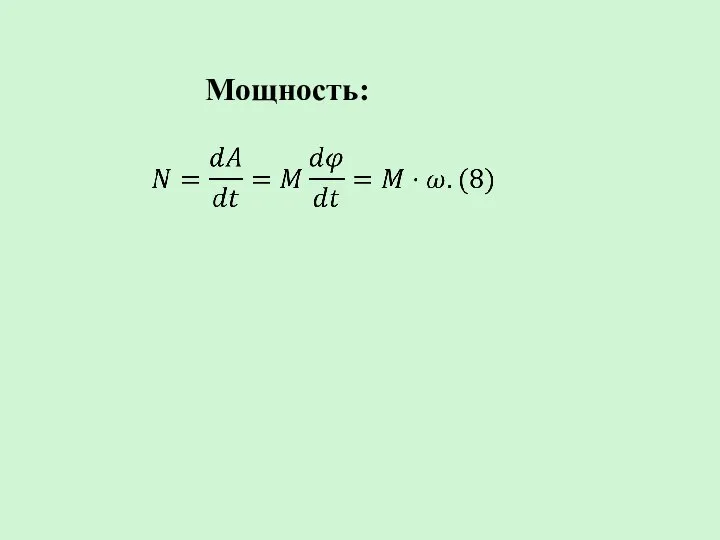

 2 Стереотипы в отношении человека работающего
2 Стереотипы в отношении человека работающего ООО ПолимерСтройРесурс. Производство и продажа строительного блока Теплоблок, Теплостен, Экстраблок
ООО ПолимерСтройРесурс. Производство и продажа строительного блока Теплоблок, Теплостен, Экстраблок Ораторское мастерство и искусство публичных выступлений
Ораторское мастерство и искусство публичных выступлений ИНТЕГРАЦИЯ проекта «Социальная карта Башкортостана» с проектом «Универсальная электронная карта» в рамках предоставления госуд
ИНТЕГРАЦИЯ проекта «Социальная карта Башкортостана» с проектом «Универсальная электронная карта» в рамках предоставления госуд Глагол to be в настоящем времени
Глагол to be в настоящем времени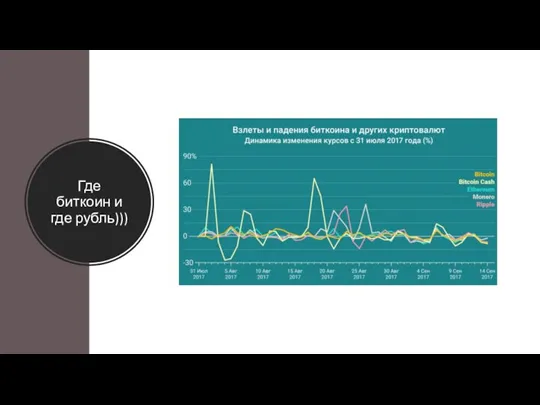 Где биткоин и где рубль
Где биткоин и где рубль Тренировочные упражненияпо орфографии
Тренировочные упражненияпо орфографии 8 декабря 1991 года в Беловежской пуще (Белоруссия) прекращение деятельности СССР и подписание соглашения о создании Содружества Нез
8 декабря 1991 года в Беловежской пуще (Белоруссия) прекращение деятельности СССР и подписание соглашения о создании Содружества Нез Великие зарубежные кинорежиссеры
Великие зарубежные кинорежиссеры Милостив и жесток государь Иван Васильевич Грозный
Милостив и жесток государь Иван Васильевич Грозный Легкая атлетика-королева спорта
Легкая атлетика-королева спорта Организационно-правовые основы деятельности любительских объединений. Тема 6
Организационно-правовые основы деятельности любительских объединений. Тема 6 Биологическое действие радиоактивных излучений
Биологическое действие радиоактивных излучений Государственный Рязанский приборный завод
Государственный Рязанский приборный завод Марийские национальные обычаи и костюмы.
Марийские национальные обычаи и костюмы. Содержание и организация контрольно-оценочной деятельности в 5-6-х классах РО(проблемная лекция)
Содержание и организация контрольно-оценочной деятельности в 5-6-х классах РО(проблемная лекция) Площади многоугольников. Решение задач. Урок 15
Площади многоугольников. Решение задач. Урок 15 Дзержинский Феликс Эдмундович
Дзержинский Феликс Эдмундович Фреш Чикен воппер - Маркировка ФК
Фреш Чикен воппер - Маркировка ФК Артефакт российской культуры: фильм Майор Гром: Чумной Доктор
Артефакт российской культуры: фильм Майор Гром: Чумной Доктор тест: Фразовые глаголы
тест: Фразовые глаголы Wine Diesel American Film Maker, Produzent, Drehbuchautor und Regisseu
Wine Diesel American Film Maker, Produzent, Drehbuchautor und Regisseu Тайo миян чужан му!
Тайo миян чужан му! Интегрированный урок по повести А.С.Пушкина «Метель»
Интегрированный урок по повести А.С.Пушкина «Метель» Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Сложение смешанных чисел: теория и практика
Сложение смешанных чисел: теория и практика Модели за соработка и учество на локално ниво
Модели за соработка и учество на локално ниво Достоинства леммы Маркова и неравенства Чебышева при оценивании риска
Достоинства леммы Маркова и неравенства Чебышева при оценивании риска