Содержание
- 2. Как работать над тестом ЕГЭ Внимательно прочитать задание Задать себе вопрос: Что я решаю?(уравнение, неравенство, тождество
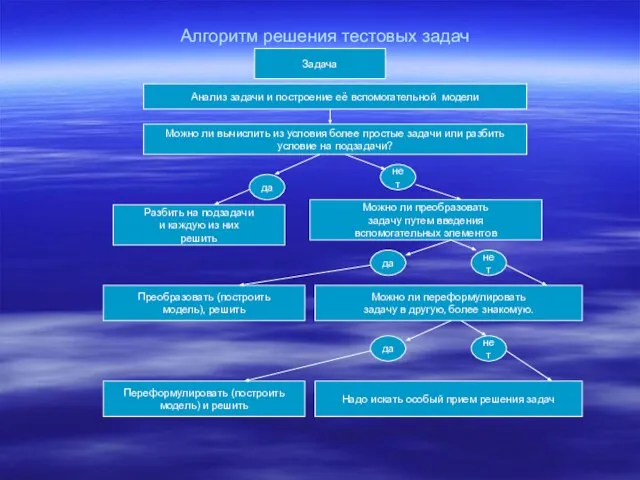
- 3. Алгоритм решения тестовых задач Задача Анализ задачи и построение её вспомогательной модели Можно ли вычислить из
- 4. Алгоритм решения задач на смеси. х – масса первого раствора, у – масса второго раствора, (х
- 5. Алгоритм решения иррациональных уравнений Нахожу ОДЗ переменной (или делаю проверку) Возвожу обе части уравнений в квадрат
- 6. I. Уединение радикала и возведение в степень. Решить уравнение: Рассмотрим уравнение системы х2– 17х + 66
- 7. Тригонометрические уравнения В курсе алгебры вычленяют 12 видов уравнений: Простейшие уравнения и уравнения сводящиеся к простейшим.
- 8. Какое уравнение называется показательным? (Уравнение , содержащие переменную и показательную степени, называется показательным.) На какой теореме
- 9. Задачи на преобразование Тождественно равными выражениями называться такие выражения, которые получаются одно из другого в результате
- 10. Логарифмические уравнения и неравенства ОДЗ переменной x Получим в обеих частях уравнения (неравенства) логарифмы с одинаковым
- 11. Пожелание выпускникам При желании можно объять необъятное Помни: глаза боятся, а руки делают Стремись, старайся, систематизируй
- 13. Скачать презентацию









 Г. Киров, 10 марта 2010г. Сети, в которые попадают люди … Люди, которые попадают в сети Выступление Управляющего партнера Агентства «Социальные Сети» Дениса. - презентация
Г. Киров, 10 марта 2010г. Сети, в которые попадают люди … Люди, которые попадают в сети Выступление Управляющего партнера Агентства «Социальные Сети» Дениса. - презентация Головные уборы
Головные уборы Розвиток технологій т’юторської діяльності студентів як фактору формування самостійної пізнавальної активності
Розвиток технологій т’юторської діяльності студентів як фактору формування самостійної пізнавальної активності Компания «Бегун»Краткая информация - 2009
Компания «Бегун»Краткая информация - 2009 Декоративно-прикладная обработка древесины
Декоративно-прикладная обработка древесины Скаты
Скаты Официально-деловой стиль
Официально-деловой стиль границы россии (2)
границы россии (2) Equivalence
Equivalence  Арт завод Платформа
Арт завод Платформа ДИЕТА И ЗДОРОВЬЕ.
ДИЕТА И ЗДОРОВЬЕ. Реабилитация несовершеннолетних через включение их в социальные проекты
Реабилитация несовершеннолетних через включение их в социальные проекты Презентация «Немного о кошках..." выполнена преподавателями образовательных учреждений Новосибирской области в рамках проекта По
Презентация «Немного о кошках..." выполнена преподавателями образовательных учреждений Новосибирской области в рамках проекта По КУПОНЫ В КАЖДЫЙ ЧЕК
КУПОНЫ В КАЖДЫЙ ЧЕК 수정사항 20221002
수정사항 20221002 Хохломская роспись
Хохломская роспись Соц_Пр_УЛ_2013.ppt
Соц_Пр_УЛ_2013.ppt Разработка и изготовление комплекта вязаных аксессуаров
Разработка и изготовление комплекта вязаных аксессуаров Спешл фо кидс v.2.1
Спешл фо кидс v.2.1 Протоиерей Виктор (Козлов), клирик храма во имя Введения во храм Пресвятой Богородицы
Протоиерей Виктор (Козлов), клирик храма во имя Введения во храм Пресвятой Богородицы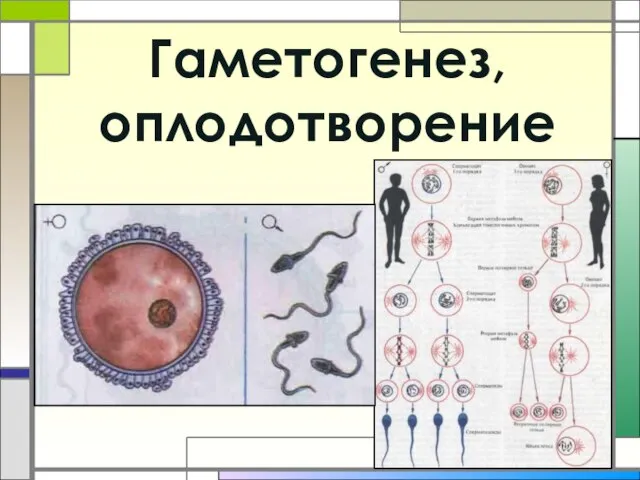 Презентация на тему Гаметогенез, оплодотворение (9 класс)
Презентация на тему Гаметогенез, оплодотворение (9 класс) Путешествие в космос
Путешествие в космос Виды и условия продуктов и услуг для частных клиентов банка. Практическое занятие 8. Вопросы практического занятия
Виды и условия продуктов и услуг для частных клиентов банка. Практическое занятие 8. Вопросы практического занятия Математик – бизнесмен
Математик – бизнесмен Презентация на тему Последний день в Белогорской крепости. Великодушие Пугачева
Презентация на тему Последний день в Белогорской крепости. Великодушие Пугачева Презентация на тему Внутренняя среда организма
Презентация на тему Внутренняя среда организма Российская империя в начале XX века
Российская империя в начале XX века право 4 урок, 10 класс-1
право 4 урок, 10 класс-1