Содержание
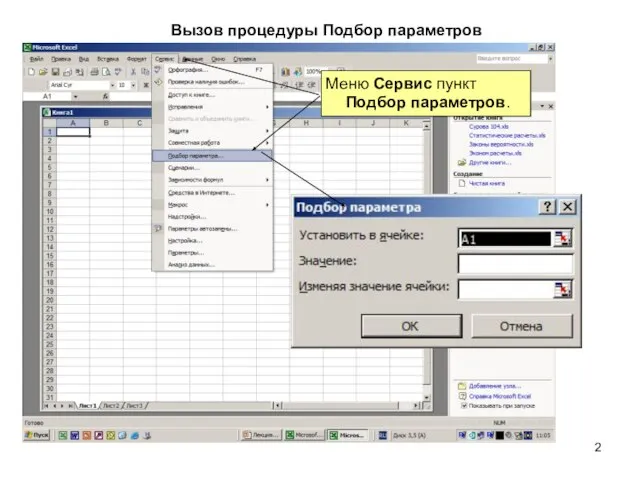
- 2. Вызов процедуры Подбор параметров Меню Сервис пункт Подбор параметров.
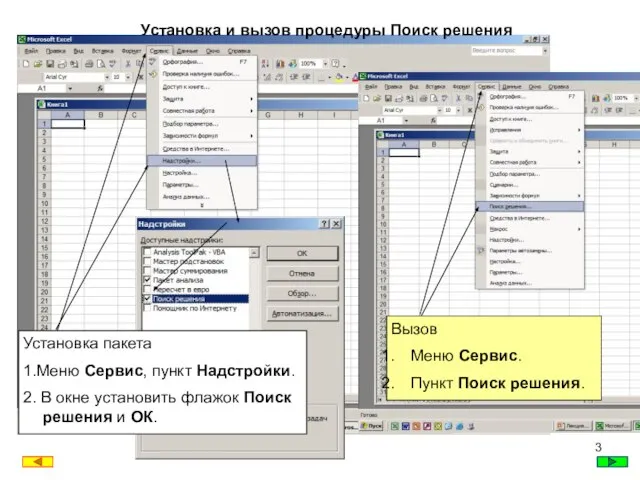
- 3. Установка и вызов процедуры Поиск решения Вызов Меню Сервис. Пункт Поиск решения. Установка пакета 1.Меню Сервис,
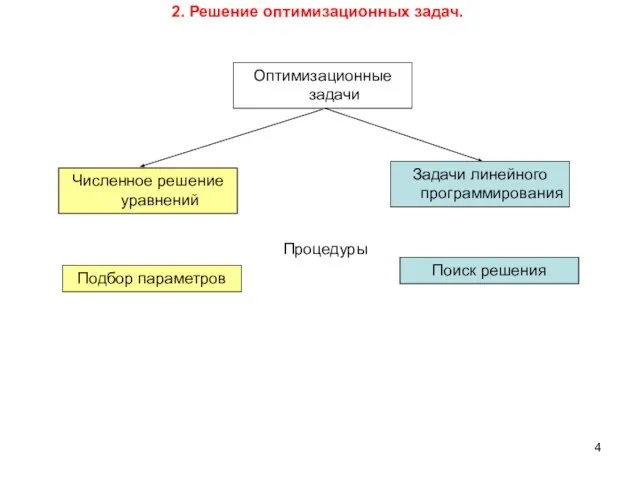
- 4. 2. Решение оптимизационных задач. Оптимизационные задачи Численное решение уравнений Задачи линейного программирования Подбор параметров Поиск решения
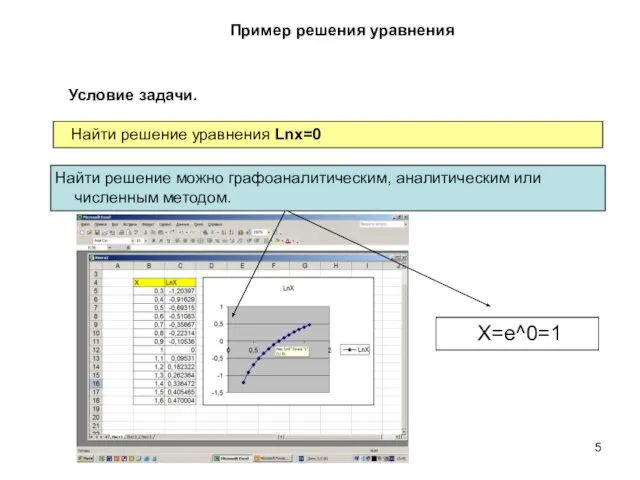
- 5. Пример решения уравнения Условие задачи. Найти решение уравнения Lnx=0 Найти решение можно графоаналитическим, аналитическим или численным
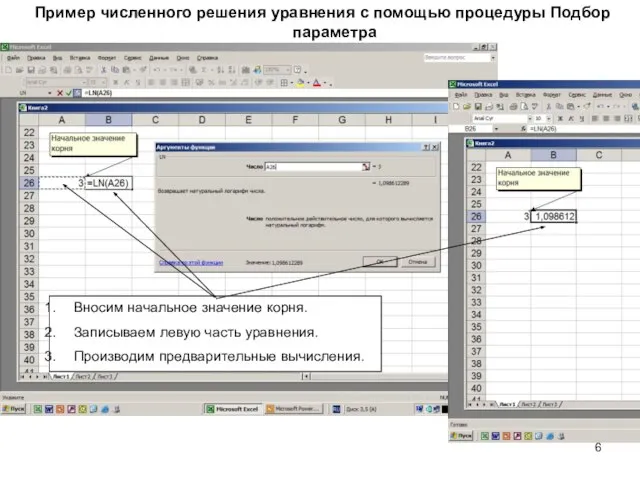
- 6. Вносим начальное значение корня. Записываем левую часть уравнения. Производим предварительные вычисления. Пример численного решения уравнения с
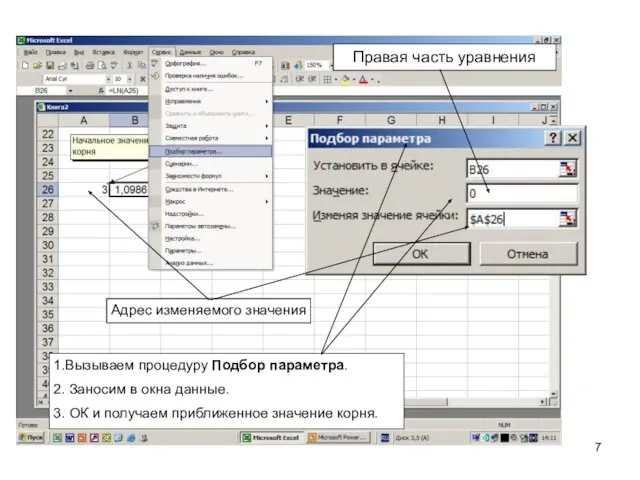
- 7. Правая часть уравнения Адрес изменяемого значения 1.Вызываем процедуру Подбор параметра. 2. Заносим в окна данные. 3.
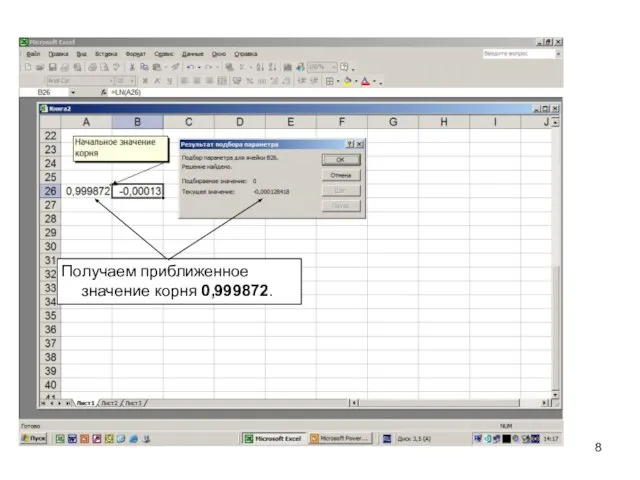
- 8. Получаем приближенное значение корня 0,999872.
- 9. В задаче линейного программирования все функции линейны. Требуется найти значения F(X), которые максимизируют или минимизируют целевую
- 10. Методика решения задачи линейного программирования 1.Определение параметров задачи в соответствии с общей постановкой задачи. 2. Введение
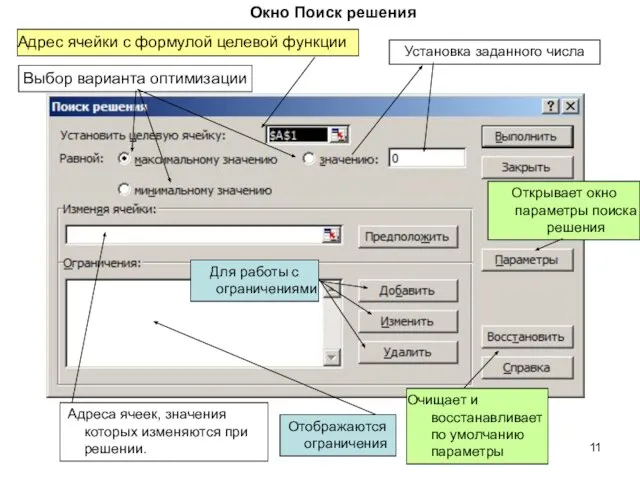
- 11. Окно Поиск решения Адрес ячейки с формулой целевой функции Выбор варианта оптимизации Установка заданного числа Адреса
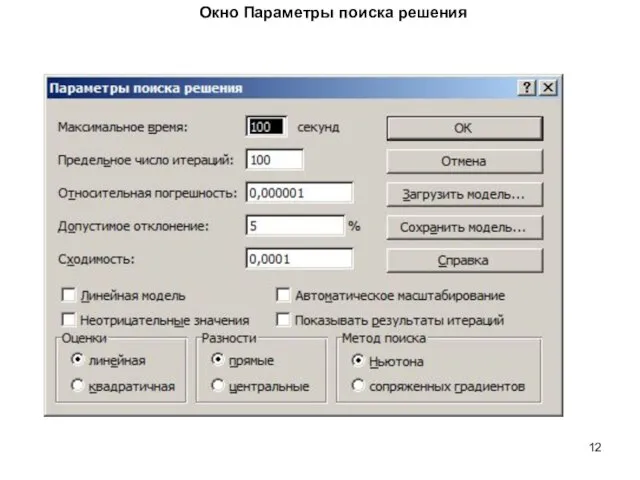
- 12. Окно Параметры поиска решения
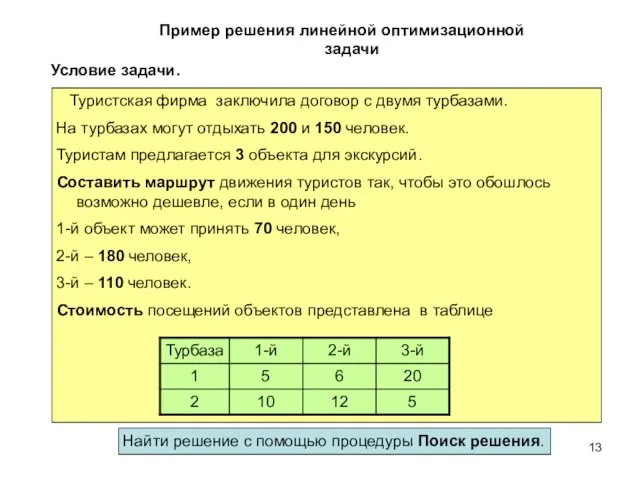
- 13. Пример решения линейной оптимизационной задачи Условие задачи. Туристская фирма заключила договор с двумя турбазами. На турбазах
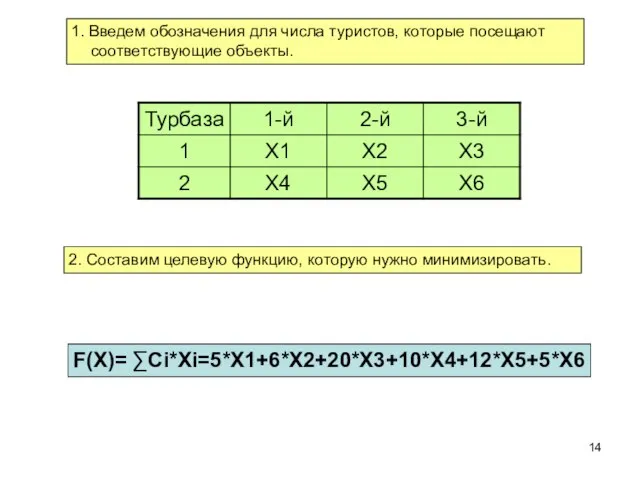
- 14. 1. Введем обозначения для числа туристов, которые посещают соответствующие объекты. 2. Составим целевую функцию, которую нужно
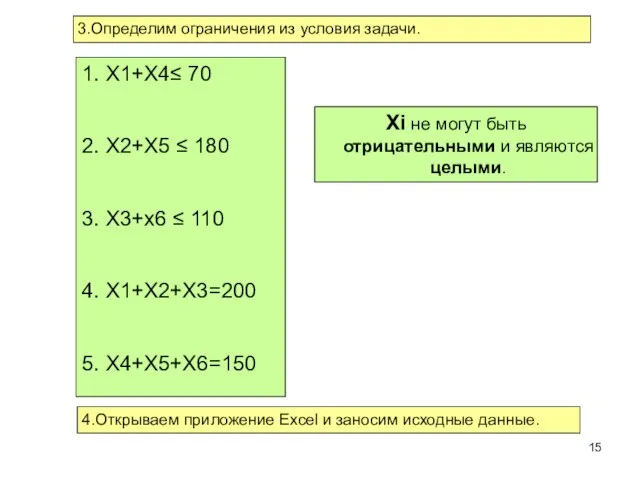
- 15. 3.Определим ограничения из условия задачи. 1. Х1+Х4≤ 70 2. Х2+Х5 ≤ 180 3. Х3+х6 ≤ 110
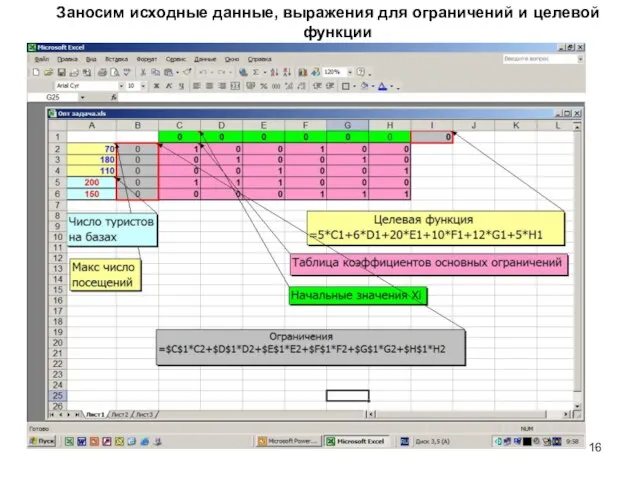
- 16. Заносим исходные данные, выражения для ограничений и целевой функции
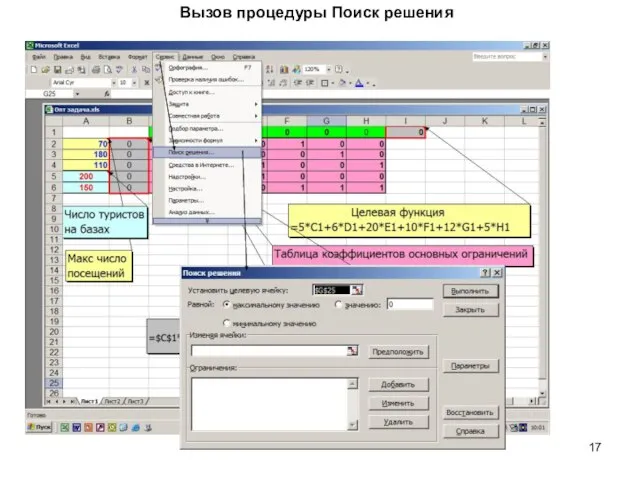
- 17. Вызов процедуры Поиск решения
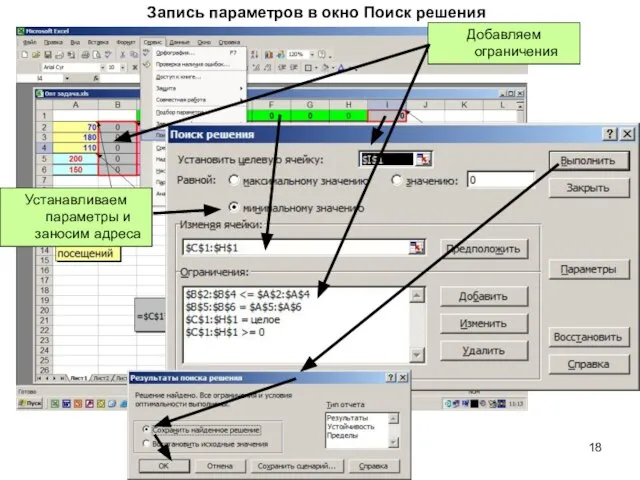
- 18. Запись параметров в окно Поиск решения Устанавливаем параметры и заносим адреса Добавляем ограничения
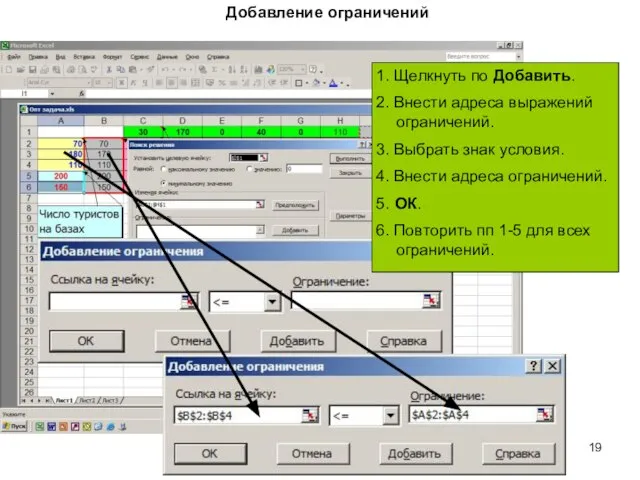
- 19. Добавление ограничений 1. Щелкнуть по Добавить. 2. Внести адреса выражений ограничений. 3. Выбрать знак условия. 4.
- 21. Скачать презентацию


 Гражданское право
Гражданское право Миокардиты и кардиомиопатии
Миокардиты и кардиомиопатии Проект Ориентир: Ямал
Проект Ориентир: Ямал KU-3 (Ку три) Система управления мультимедиа тренингами, моделирующими играми и динамическими тестами.
KU-3 (Ку три) Система управления мультимедиа тренингами, моделирующими играми и динамическими тестами. Презентация на тему Мирное освоение космоса
Презентация на тему Мирное освоение космоса  4 день. Запоминание штатов США. Чертоги разума
4 день. Запоминание штатов США. Чертоги разума Межрегиональная конференция «Сопровождение одаренного ребенка в региональном образовательном пространстве»
Межрегиональная конференция «Сопровождение одаренного ребенка в региональном образовательном пространстве» Преобразованиеграфиков функций
Преобразованиеграфиков функций Презентация на тему Пьер Огюстен Карон де Бомарше
Презентация на тему Пьер Огюстен Карон де Бомарше Презентация
Презентация Презентация на тему Воды суши. Подземные воды
Презентация на тему Воды суши. Подземные воды Спинной мозг
Спинной мозг Представляемклуб«Изыскатели»ГОУ № 490Красногвардейского района
Представляемклуб«Изыскатели»ГОУ № 490Красногвардейского района Ячейки овощехранилища Расположенные по адресу: г.Новосибирск, Ленинский район, ул. Котовского,5/3
Ячейки овощехранилища Расположенные по адресу: г.Новосибирск, Ленинский район, ул. Котовского,5/3 Контрольные вопросы
Контрольные вопросы rvex5e0qf2kcfgmz01w1i7ity29jz3lp
rvex5e0qf2kcfgmz01w1i7ity29jz3lp Презентация на тему Реальное и фантастическое в повести Н. В. Гоголь "Заколдованное место"
Презентация на тему Реальное и фантастическое в повести Н. В. Гоголь "Заколдованное место" Закон Ома
Закон Ома Структура исследовательской работы
Структура исследовательской работы Intel “Шлях до успіху” ч1 Комп’ютерні технологіі для місцевої спільноти ЗАКЛАДАЄМО ПАРК Соціальний проект підготували учні 7-х класів:Антон, Марина, Ольга, Лариса с.Успішне Серпень 2009
Intel “Шлях до успіху” ч1 Комп’ютерні технологіі для місцевої спільноти ЗАКЛАДАЄМО ПАРК Соціальний проект підготували учні 7-х класів:Антон, Марина, Ольга, Лариса с.Успішне Серпень 2009 Новогодняя викторина 3 класс
Новогодняя викторина 3 класс Ахмед Сукарно
Ахмед Сукарно Заготовка продуктов (6 класс)
Заготовка продуктов (6 класс) Детство без жестокости и насилия
Детство без жестокости и насилия Украшения из текстиля. Комплект Горячее сердце
Украшения из текстиля. Комплект Горячее сердце Блиц-опрос
Блиц-опрос Кейс - метод
Кейс - метод Презентация на тему Моделирование как метод познания (9 класс)
Презентация на тему Моделирование как метод познания (9 класс)