Методы автоматизации доказательства NP-полноты двумерных локально зависимых задач

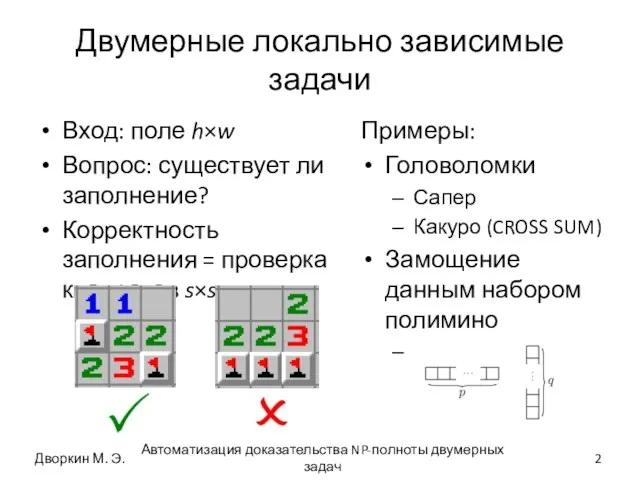
Двумерные локально зависимые задачи
Вход: поле h×w
Вопрос: существует ли заполнение?
Корректность заполнения = проверка квадратов s×s
Примеры:
Головоломки
Сапер
Какуро (CROSS SUM)
Замощение данным набором полимино
(p,q)-замощение
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Применение устройств
«На языке задачи L» выражается известная NP-полная задача
Используются «устройства» (gadgets) и провода, соединяющие их
Устройства могут
быть сложны
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Постановка задачи
Автоматизация построения устройств с заданной функциональностью
Описание наборов устройств, достаточных для доказательства NP-полноты
Программная реализация
Применение для доказательства
NP-полноты конкретных задач
N-CROSS SUM
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Сведение 1-in-3 SAT к L
Задача 1-in-3 SAT:
Вход: конъюнкция из предикатов R(A, B, C)
Вопрос: выполнима ли конъюнкция?
Удобна, поскольку истинность конъюнкций проверяется независимо
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Одинарные и двойные провода
Провод придумывается человеком, зачастую — просто
Устройство «создание провода» не всегда существует
Рассматриваются двойные провода:
«в фазе»
«в противофазе»
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

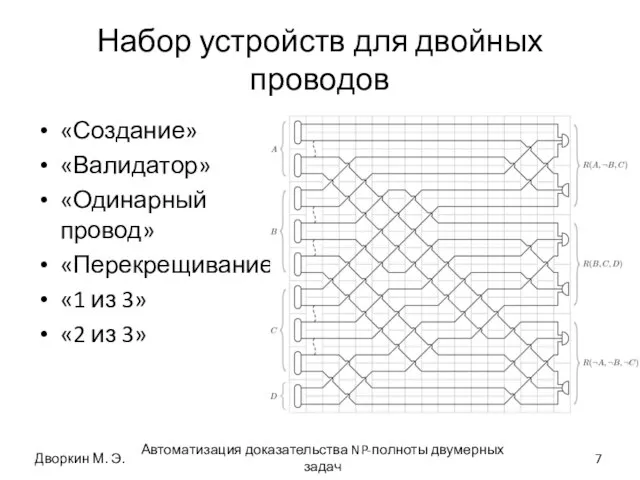
Набор устройств для двойных проводов
«Создание»
«Валидатор»
«Одинарный
провод»
«Перекрещивание»
«1 из 3»
«2 из 3»
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Динамическое программирование
по профилю
Профиль — вертикальный «срез» поля, содержит всю необходимую информацию для дальнейшей обработки поля
Прямой профиль
Проще для понимания
Громоздкий переход, большая таблица переходов
Изломанный профиль
Их число больше
Таблица переходов меньше
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Подход «перебор всех полей»
Перебрать все поля, O(|A|hw)
Для каждого проверить, является ли оно искомым устройством, O(nhwp|B|)
Итого: O(|A|hwnhwp|B|)
Улучшение: для разных полей не обрабатывать общие префиксы
Время работы: O(|A|hwnp|B|)
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Метадинамическое программирование
Рассмотрим два поля после обработки первых i клеток. Что если все совпадает?
Метапрофиль — множества достижимых профилей для каждого набора булевых значений входных проводов
После обработки i-й клетки все поля с одинаковыми метапрофилями можно отождествить
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Метадинамическое программирование
O(min(|A|hwnp|B|, |A||B|nphw2np))
Критична высота рассматриваемого поля
Если после обработки столбца то же множество метапрофилей, что и до нее, можно остановиться
Для каждого метапрофиля хранится одно поле-представитель (самое «красивое»)
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

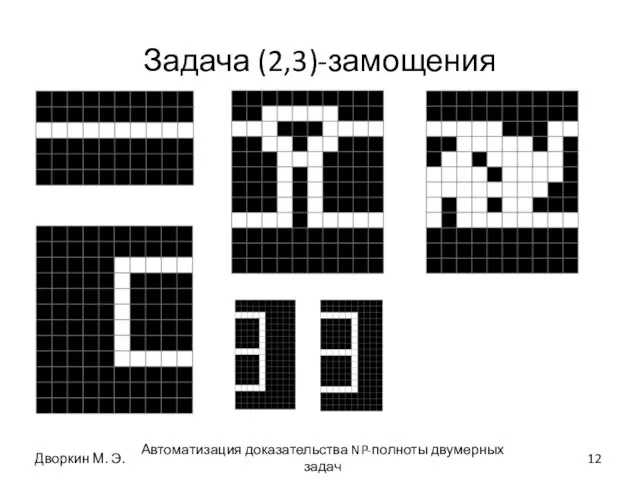
Задача (2,3)-замощения
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Задача 4-CROSS SUM (открытый вопрос)
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.

Задача 4-CROSS SUM (открытый вопрос)
Автоматизация доказательства NP-полноты двумерных задач
Дворкин М. Э.