Методы неявного перебора

Рассмотрим общую постановку задачи дискретной оптимизации
где n-мерный вектор x ∈ конечному мн. доп. решений D.
Постановка задачи
⇒ можно перебрать все решения и выбрать opt…
В методах неявного перебора доп. мн. решений разбивается на не ∅ подмн. < мощности. Затем анализируется возможность исключения этих подмн., а также улучшения найденного доп. решения (рекорда).
В результате возможно сокращение перебора доп. решений.
Метод ветвей и границ
Аддитивный алгоритм Балаша.

Метод ветвей и границ (МВГ)
Ветвлением мн. d ⊆ D наз. функцию
b : d → {d1, …, dN}, dk ⊂ d, dk ≠ ∅,
k = 1, …, N,
разбивающую мн. d на несобственные подмн.
Числовая функция H наз. нижней границей функционала f на мн. d, если:
{x} – одноэлементное мн.
Наз. рекордом, и обозн. его x0, наилучшее из найденных доп. решение. Величина f(x0) является верхней границей (ВГ) функционала задачи. Сначала рекорд x0 либо произвольное доп. решение, либо не известен.

Правила отсечения
МВГ последовательно выполняет итерации (шаги).
На очер. итер. выбирается и проверяется нек. не отсеченное мн.
В результате оно либо отбрасывается (отсекается), либо разбивается на непустые подмн. < мощности (ветвится).
Пусть t1, …, tL мн. не отсеченных подмн. решений.
(первоначально L = 1, t1 = D.)
Мн. ti, 1 ≤ i ≤ L отсекается в одном из 2-х, последовательно проверяемых, случаев:
a) если H(ti) ≥ f(x0);
b) если H({ti}) = f(ti) < f(x0). Т.е. 1-элем. мн. отсекается всегда. Последнее неравенство имеет место, т.к. 1-элем. мн. не было удалено по критерию a). Значит, в случае b) происходит смена рекорда x0 = ti и ВГ f(x0).

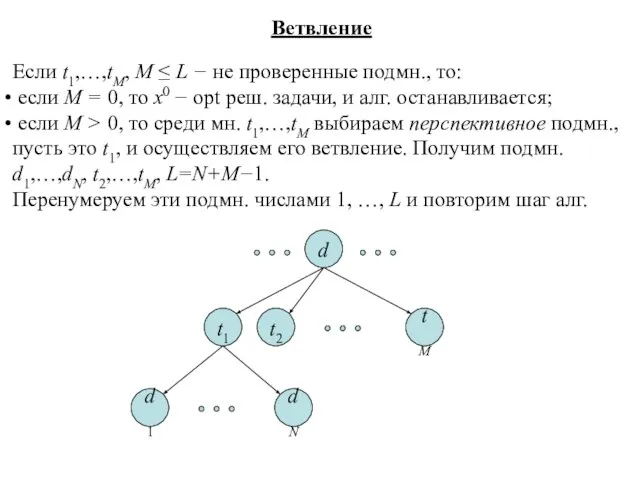
Ветвление
Если t1,…,tM, M ≤ L − не проверенные подмн., то:
если M = 0, то x0 − opt реш. задачи, и алг. останавливается;
если M > 0, то среди мн. t1,…,tM выбираем перспективное подмн., пусть это t1, и осуществляем его ветвление. Получим подмн. d1,…,dN, t2,…,tM, L=N+M−1.
Перенумеруем эти подмн. числами 1, …, L и повторим шаг алг.
d
t1
tM
d1
dN
t2

Корректность алгоритма
Теорема. Приведенный алгоритм МВГ находит решение задачи за конечное число шагов.
Доказательство. Конечность алг. ⇒ из след. 4 свойств:
1) На каж. шаге выбранное подмн. либо удаляется, либо разбивается на непустые подмн. < мощности.
2) 1-элем. мн. исключаются всегда.
3) Подмн. не проверяются > 1 раза.
4) Исходное мн. доп. решений D конечно.
Докажем opt найденного решения. Предположим противное: после остановки алгоритма, рекорд x0 не является opt решением задачи. Значит,
⇒ на каком-то шаге opt решение x* было удалено вместе с нек. мн. t на основании правила а), т.е. H(t) ≥ f(x0). Значит,
f(x*) ≥ H(t) ≥ f(x0), что противоречит предположению (*).
(*)

Реализация МВГ
Если получение ВГ сопряжено с трудностями, тогда для быстрого нахождения рекорда следует применять схему одностороннего ветвления, когда разбивается мн. min мощности.
⇒ 1-элем. мн. и доп. решение (1 рекорд) будут найдены быстро.
Мн., имеющее min НГ, может с большой вероятностью содержать решение, близкое (по функционалу) к opt, что приведет к получению хорошего рекорда (и ВГ). Выбор такого мн. для дальнейшего разбиения определяет схему всестороннего ветвления.
Если при реализации алг. критической является память, тогда схема одностороннего ветвления предпочтительнее.

Реализация МВГ
Для решения МВГ конкретной задачи следует определить:
способ представления подмн. решений; схему и способ ветвления;
алг. вычисления НГ;
метод нахождения рекорда.
Время работы алг. зависит от многих факторов. Теоретически не исключен полный перебор решений. Практически же следует найти компромисс между точностью и сложностью вычисления НГ, что позволит найти решение, близкое к opt, за приемлемое время. Более точное вычисление НГ может позволить отсечь больше решений, но потребует и больше времени, что может привести к длительному выполнению 1 итерации.

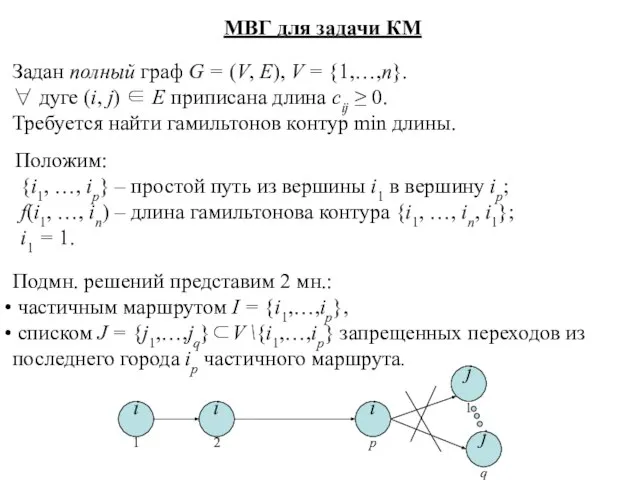
МВГ для задачи КМ
Задан полный граф G = (V, E), V = {1,…,n}.
∀ дуге (i, j) ∈ E приписана длина cij ≥ 0.
Требуется найти гамильтонов контур min длины.
Подмн. решений представим 2 мн.:
частичным маршрутом I = {i1,…,ip},
списком J = {j1,…,jq}⊂V \{i1,…,ip} запрещенных переходов из последнего города ip частичного маршрута.
Положим:
{i1, …, ip} – простой путь из вершины i1 в вершину ip;
f(i1, …, in) – длина гамильтонова контура {i1, …, in, i1};
i1 = 1.
i1
i2
ip
j1
jq

Ветвление
Если p < n – 1, то 0 ≤ q ≤ n – p – 2.
Если же p = n – 1, то q = 0, т.е. мн. (I, J) определяют ед. решение.
Функция ветвления b делит мн. гам. контуров (I, J), на 2 подмн.
Для этого выбирается некоторая вершина i ∈ V′ = V \ (I ∪ J).
Если кроме i в множестве V′ ∃! вершина k, то:
I = {i1, …, ip, i}, J = ∅ , а другое мн. I = {i1, …, ip, k}, J = ∅.
Если в V′ > 2 эл., то 1 мн. I = {i1, …, ip, i}, J = ∅,
а 2 мн. I = {i1, …, ip}, J = {j1, …, jq, i}.
i1
ip
i
k
i1
ip
i

Вычисление НГ
Введем матрицу
где
для незапрещенных
дуг, и
для запрещенных. Вычислим
Лемма. Если {i1, …, in, i1} – гам. контур мн. (I, J), то
f(i1, …, in) ≥ H(I, J).
Доказательство. Из определения αi и βj имеем:
≥ 0

Вычисление НГ
Функция
удовлетворяет
и 2-му свойству НГ. H({x}) = f(x), т.к. в случае p=n− 1, имеем
αn-1 = cn-1,n , αn = cn1 , β1 = 0, βn= 0.
Для произвольного мн. (I, J) можно найти доп. решение, например, используя жадный алгоритм: “иди в ближайшую вершину, где еще не был”, начиная с вершины p и учитывая запреты J…
Выбор вершины i для ветвления мн. (I, J) …

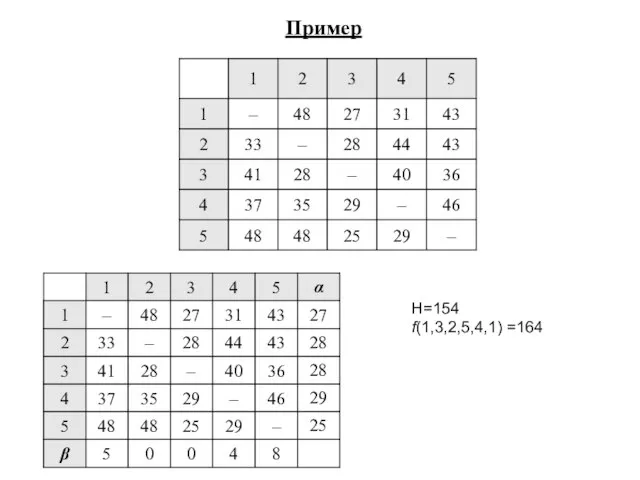
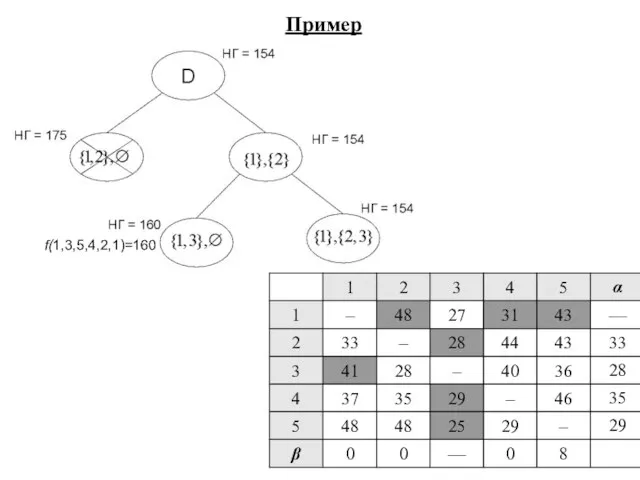
H=154
f(1,3,2,5,4,1) =164
Пример

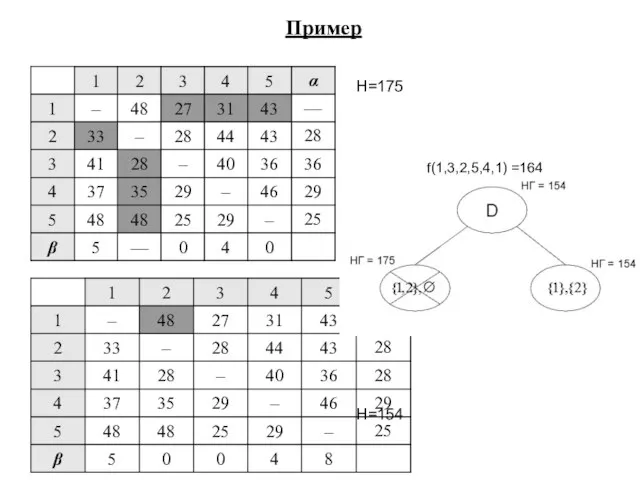
H=175
H=154
f(1,3,2,5,4,1) =164
Пример

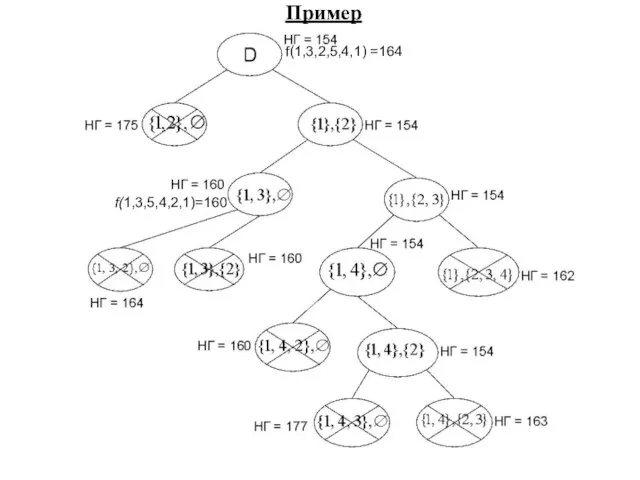
f(1,3,5,4,2,1)=160
Пример

f(1,3,2,5,4,1) =164
f(1,3,5,4,2,1)=160
Пример

2-й способ построения НГ для задачи КМ
Задача о назначениях. Имеется n работ и n исполнителей,
cij ≥ 0 – затраты, связанные с назначением i-го исп. на j-ю работу.
Каждая работа должна быть выполнена 1 исполнителем, и каждый исполнитель должен выполнить 1 работу.
Требуется назначить исп. на работы : общие затраты min.
xij=1, если исполнитель i назначен на работу j;
xij=0 в противном случае.
T=O(n3).
Предположим, что cij = длине перехода i → j и положим
cii = +∞, i = 1, …, n. ⇒ Z является НГ для ц.ф. задачи КМ

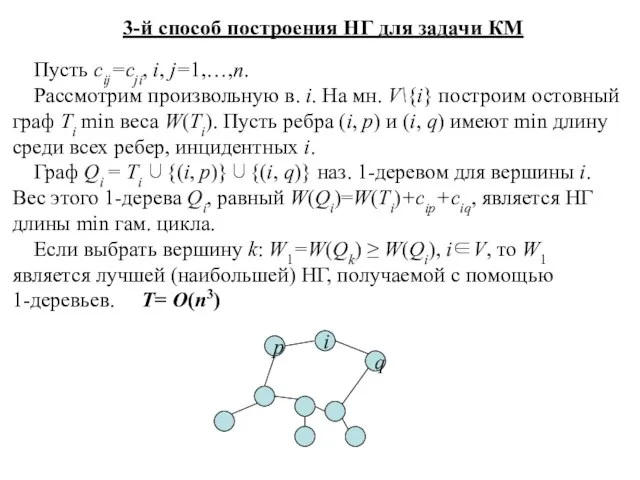
3-й способ построения НГ для задачи КМ
Пусть cij=cji, i, j=1,…,n.
Рассмотрим произвольную в. i. На мн. V\{i} построим остовный граф Ti min веса W(Ti). Пусть ребра (i, p) и (i, q) имеют min длину среди всех ребер, инцидентных i.
Граф Qi = Ti ∪{(i, p)}∪{(i, q)} наз. 1-деревом для вершины i.
Вес этого 1-дерева Qi, равный W(Qi)=W(Ti)+cip+ciq, является НГ длины min гам. цикла.
Если выбрать вершину k: W1=W(Qk) ≥ W(Qi), i∈V, то W1 является лучшей (наибольшей) НГ, получаемой с помощью
1-деревьев. T= O(n3)
i
p
q

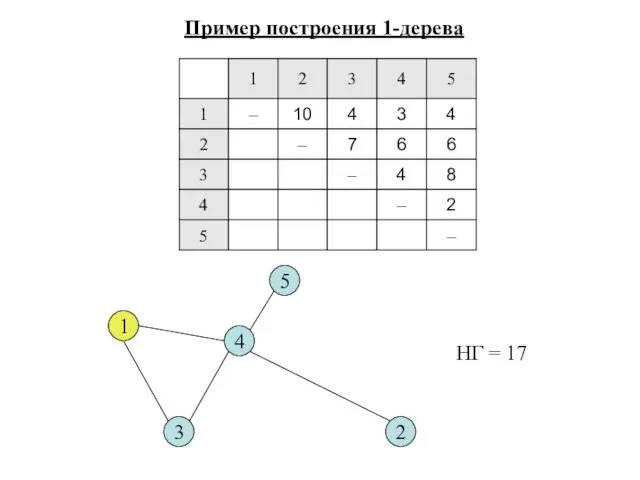
Пример построения 1-дерева
1
2
3
4
5
НГ = 17

Аддитивный алгоритм Балаша
(1)
(2)
Наз. решением мн. {xj : xj=1, j∈N1; xj=0, j∈N\N1, N={1,…,n}}.
Решение является допустимым, if выполняются неравенства (2).
Пусть 0≤c1≤c2≤…≤cn. (if ∃ j : cj<0, то → yj=1–xj)
Доп. решение x доминирует доп. решение y, если Z(x) < Z(y).
Если решения доминируются лучшим найденным допустимым решением (рекордом), то их можно отбросить.

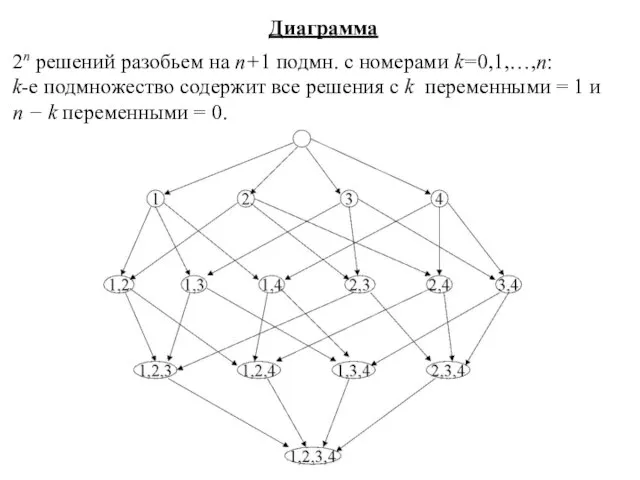
Диаграмма
2n решений разобьем на n+1 подмн. с номерами k=0,1,…,n:
k-е подмножество содержит все решения с k переменными = 1 и
n − k переменными = 0.

Упорядоченность решений
при k=0, подмн. решений состоит из 1 решения х = 0;
при k=1, подмн. решений включает n решений, в которых xi=1; xj=0, j≠ i; i=1,…,n;
k-е подмножество состоит из
На диаграмме каж. вершина, содержащая список N1, представляет решение, в котором переменные с индексами из N1 равны 1, а остальные – 0. Так вершина (1,3) соответствует решению
x1=x3=1; x2=x4=0.
решений.
Если в диаграмме ∃ путь из u в v, то в. u наз. предшествующей для в. v, а v - следующей за u.
⇒ решения частично упорядочены.

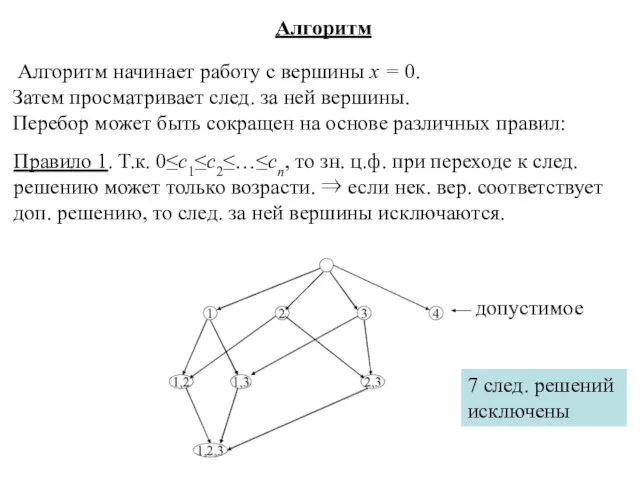
Алгоритм
Алгоритм начинает работу с вершины х = 0.
Затем просматривает след. за ней вершины.
Перебор может быть сокращен на основе различных правил:
Правило 1. Т.к. 0≤c1≤c2≤…≤cn, то зн. ц.ф. при переходе к след. решению может только возрасти. ⇒ если нек. вер. соответствует доп. решению, то след. за ней вершины исключаются.
допустимое
7 след. решений
исключены

Правила отсечения
Правило 2. Пусть
Z* − min (рекордное) зн. ц.ф. на найденных доп. реш.,
ZQ – зн. ц.ф. в вершине VQ , где xj=1, j∈Q; xj=0, j∈ N\Q.
Если для некоторого r имеет место неравенство ZQ+cr >Z*, то достаточно проверять только те следующие вершины, в кот. xr=xr+1=xn=0 (в силу неравенств 0≤c1≤c2≤…≤cn).
Правило 3. Пусть вер. VQ задает реш. xj=1, j∈Q; xj=0, j∈N\Q.
⇒ все след. в. должны иметь xj=1, j∈Q. Такие пер. наз. фиксированными для след. в. Остальные - свободными.
Вершина VQ может оказаться недоп. из-за нек. неравенств (2).
Пример. Q={1,2} и –x1–x2+x3+x4≥1.
Даже, если у след. вершин переменные x3=x4=1, то данное неравенство не может быть выполнено.
⇒ все след. за VQ вершины могут быть исключены.