Методы погашения долгосрочной задолженности

Методы погашения долгосрочной задолженности
Методы погашения долгосрочной задолженности
Единоразовое погашение
Возврат разовым платежом без накопления на счете
Возврат разовым платежом методом накопления фонда
Погашение основного долга в рассрочку
Возврат основного долга равными суммами долга
Возврат равными уплатами долга с процентами
Погашение ипотечного кредита
Возврат потребительского кредита по “схеме 78”

Методы погашения долгосрочной задолженности

Методы погашения долгосрочной задолженности
Метод формирования погасительного фонда
Подставив R в формулу (1), получим
Yt = D*i + D/sg,n = D(i + 1/sg,n) -значение срочной уплаты при начислении на основной долг простых процентов
Для расчета накопленных за t лет сумм погасительного фонда используется формула наращенных сумм постоянных рент:
В случае формирования фонда по схеме простых процентов, режиме платежей по m и р-кратной ренте, используются соответствующие расчетные формулы.

Методы погашения долгосрочной задолженности
Метод формирования погасительного фонда

Методы погашения долгосрочной задолженности
Метод формирования погасительного фонда

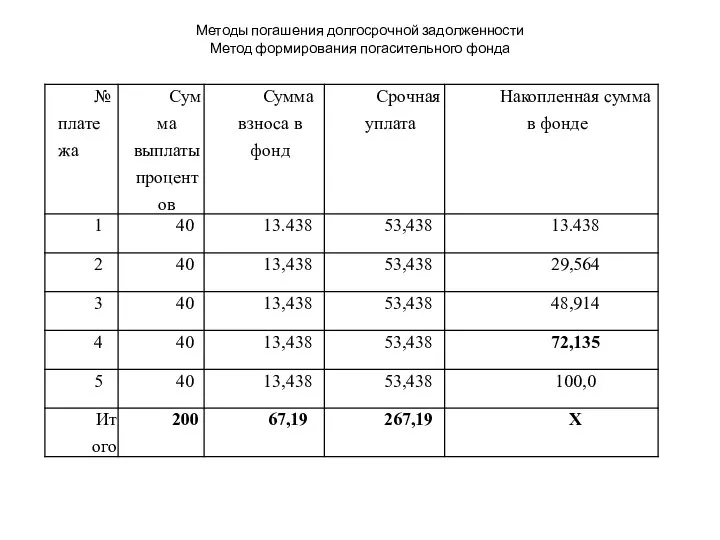
Методы погашения долгосрочной задолженности
Метод формирования погасительного фонда
Сумма накопления в фонде Wt
рассчитывается наращиванием ежегодных взносов R=13,438 тыс. рублей по формуле (3.2) либо по известным формулам наращенной ренты за соответствующий период времени.
Например, наращенная сумма в фонде за 4 года равна
Последовательным наращиванием
W4 = 48,914(1+0,2)+13,438 = 72,135
или по формуле наращенной величины
W4 = 13,438*((1+0,2)4 – 1)/0,2 = 72,135

Методы погашения долгосрочной задолженности
Погашение равными суммами долга
При годовом погашении размеры платежей по основному долгу будут равны
D/n=R1=R2=…=Rn=const=R
Остаток основного долга в начале каждого расчетного периода (Dк) определится как
Dк = D – R (к – 1)
D - сумма первоначального долга,
к - номер расчетного периода.
Величина срочной уплаты в каждом расчетном периоде равна
Yк = Dк*i + R
Подставив в (3.4) значение Dк, получим
Yк = Dк*i + R
Yк = (D-R(к-1))*i + R (3.3)
При погашении задолженности чаще, чем раз в год при расчете появляется
параметр р, отражающий частоту платежей в течение года, корректирующий
размер выплаты по долгу
R = D/np
И размер выплаты процентов соответственно
Iк = Dк*i/p

Методы погашения долгосрочной задолженности
Погашение равными суммами долга
Пример.
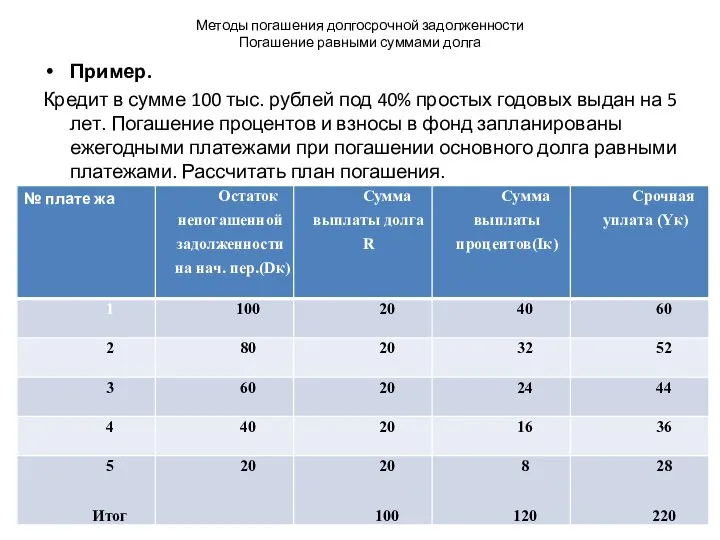
Кредит в сумме 100 тыс. рублей под 40% простых годовых выдан на 5 лет. Погашение процентов и взносы в фонд запланированы ежегодными платежами при погашении основного долга равными платежами. Рассчитать план погашения.

Методы погашения долгосрочной задолженности
Погашение равными суммами долга
Суммы, идущие на погашение долга, увеличиваются во времени:
Rк+1 = Rк(1+i) (для годовых выплат).
Размер роста Rк соответствует сумме уменьшения выплачиваемых процентов по долгу.
Платежи по погашению долга образовывают ряд:
R1, R1(1+i), R1(1+i)2, R1(1+i)3, ....,R1(1+i)n.
Используя этот ряд, несложно определить размер погашенного долга на любой момент времени t (после очередной выплаты).
t-1
Wt = ∑ R1(1+i)к
К=0
Соответственно, остаток непогашенной задолженности на начало периода t будет равен разнице D и Wt

Методы погашения долгосрочной задолженности
Погашение равными срочными уплатами (аннуитетом)

Методы погашения долгосрочной задолженности
Погашение равными срочными уплатами (аннуитетом)
Пример
Тот же. Погашение равными суммами вместе с процентами.
Y= 100*0,4/(1-1,4-5) = 49,136 тыс. рублей
I1 = D*i = 100*0,4 = 40 тыс.руб.
R1 = Y-I1=49,136-40=9,136 тыс.руб.
Остаток непогашенного долга на начало 2 года рассчитывается как разница между начальной суммой долга и размером погашенной задолженности первым платежом:
D2 = D – R1 = 100 – 9,136 = 90,864 тыс. рублей
Далее сумма процентов в структуре срочной уплаты 49,136 тыс. рублей определяется из расчета процентов от остатка непогашенной задолженности D2 = 90,864 тыс. рублей, что соответствует сумме I2 = 90,864*0,4 = 36,3456 тыс. рублей

Методы погашения долгосрочной задолженности
Погашение равными срочными уплатами (аннуитетом)

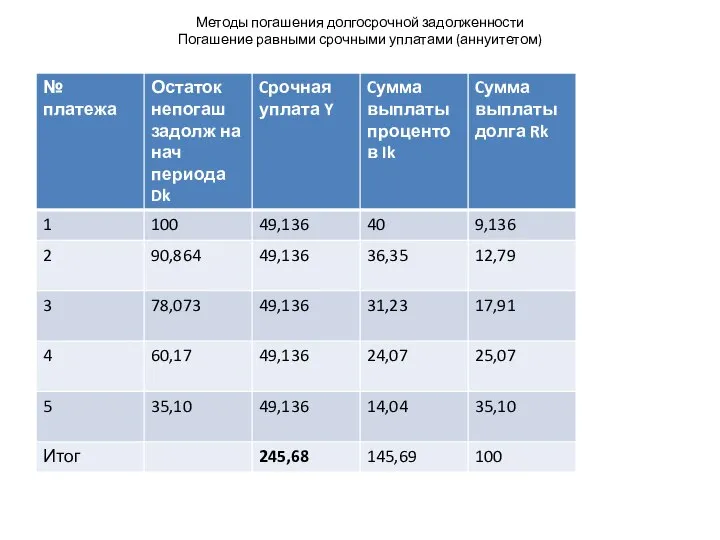
Методы погашения долгосрочной задолженности
Погашение равными срочными уплатами (аннуитетом)
Суммы, идущие на погашение долга, увеличиваются во времени:
Rк+1 = Rк(1+i) (для годовых выплат).
Размер роста Rк соответствует сумме уменьшения выплачиваемых процентов по долгу.
Платежи по погашению долга образовывают ряд:
R1, R1(1+i), R1(1+i)2, R1(1+i)3, ....,R1(1+i)n.
Используя этот ряд, несложно определить размер погашенного долга на любой момент времени t (после очередной выплаты).
t-1
Wt = ∑ R1(1+i)к
К=0
Соответственно, остаток непогашенной задолженности на начало периода t будет равен разнице D и Wt
Пример
Определить размер погашенного долга за 3 года и остаток к погашению до конца периода. (Условия предыдущей задачи).
Сумма взноса по погашению долга в первом периоде составляет R1=9,136 т. р.
Объем погашения за 3 года
Wз=9,136* s3,40 =9,136*{(1+0,4)3-1 }/0,4=39,83 т.руб.
Остаток к погашению равен
D-Wз=100 - 39,83=60,17 т.руб., что соответствует данным таблицы.

Методы погашения долгосрочной задолженности
Погашение схема «78»
Пусть выдан потребительский кредит в сумме D на n лет. Общая сумма задолженности вместе с процентами за весь срок погашения равна
S = D (1+n*i).
Поскольку погашение ведется равными долями от общей суммы задолженности, размер срочной уплаты рассчитывается
Y = S/n
При режиме погашения р раз в год - Y = S/nр.
В срочной уплате выделяются части, направленные на погашение процентов It и основного долга Rt: Y = It + Rt. При расчете плана погашения определяется размер процентного платежа, а затем - сумма, направленная на погашение основного долга:
Rt = Y – It.

Методы погашения долгосрочной задолженности
Погашение схема «78»
Процентные выплаты расположены в последовательности nр/Q, nр-1/Q,...,1/Q.
Величина Q - сумма арифметической прогрессии 1,2,3,...,nр с первым членом 1 и разностью 1. Эта сумма равна
Q=nр(nр+1)/2.
Например, при погашении задолженности в течение 2 лет ежемесячными платежами “правило 78” преобразуется в “правило 300”:
Q=2*12*(2*12+1)/2=:24*2%/2=300
и процентные платежи в срочных уплатах расположены в последовательности
I1 = 24/300*I, I2 = 23/300*I,... ,I24 = 1/300*I.

Методы погашения долгосрочной задолженности
Погашение схема «78»
Пример.
Погашение потребительского кредита ведется в течение 5 лет. Сумма кредита - 100 тыс. рублей, проценты - 20% годовых. Погашение ежемесячное.
S=D( 1+in)=100( 1+0,2*5)=200 т. рублей.
Сумма процентов - I=100 т. рублей
Срочная уплата Y=200/5*12=3,33 т. рублей
Q=5*12*61/2=1830
Для первого платежа находим
I1=60/1830*100=3,27 т. рублей, R1=3,33-3,27=0,06 т. рублей

Методы погашения долгосрочной задолженности
Погашение схема «78»

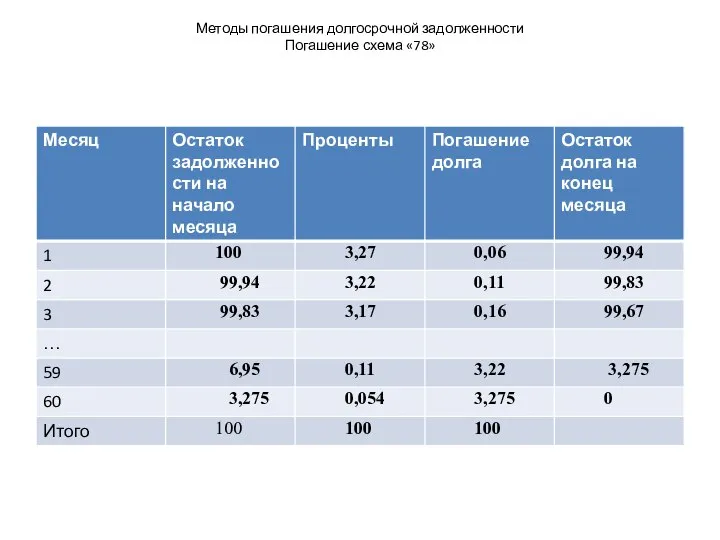
Методы погашения долгосрочной задолженности
Грант-элемент - это условная потеря заимодавца, которая связана с применением более низкой процентной ставки, чем ставка кредитного рынка.
Грант-элемент определяется в двух видах - абсолютной и относительной величины.
Размер абсолютного грант-элемента находим следующим образом:
W = D - G (G-дисконтированная по ставке кредитного рынка величина льготного потока платежей).
Относительный грант-элемент:
w = W/D = 1 – G/D