Содержание
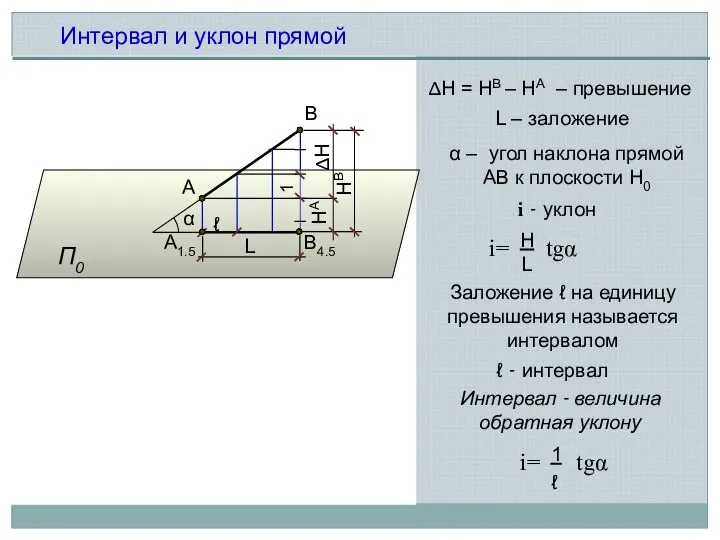
- 2. А В4.5 П0 А1.5 В Интервал и уклон прямой ∆H = НВ – НА – превышение
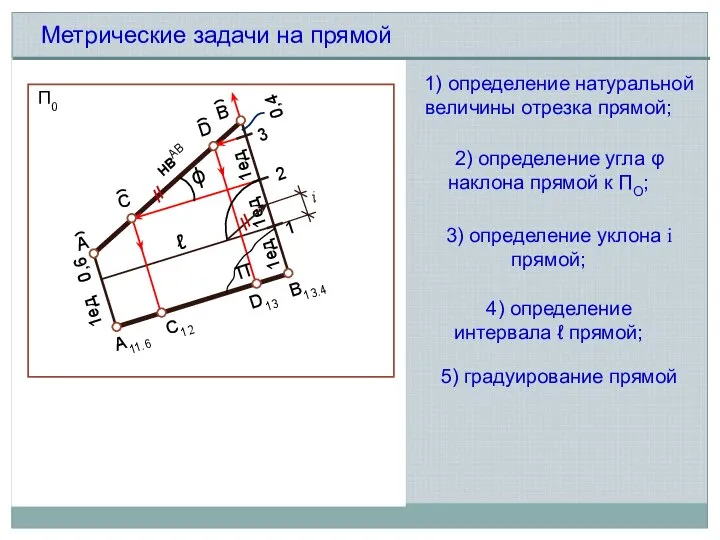
- 3. Метрические задачи на прямой 5) градуирование прямой 1) определение натуральной величины отрезка прямой; 2) определение угла
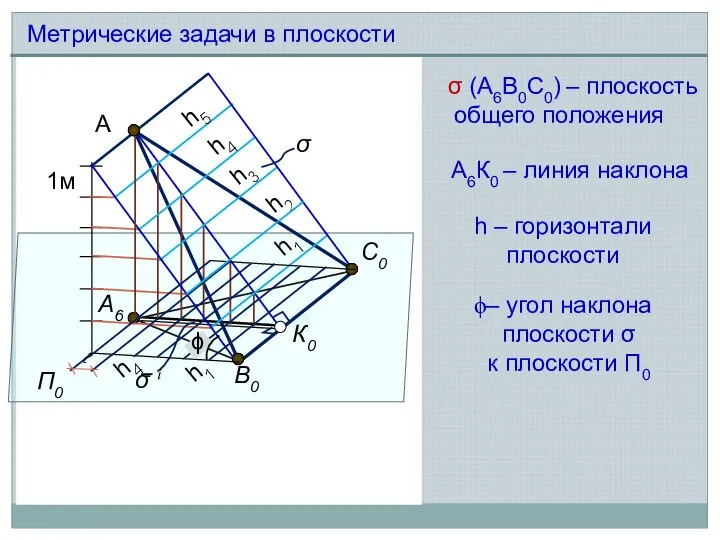
- 4. А А6 П0 В0 С0 К0 σ 1м h5 h4 h3 h2 h1 σ i σ
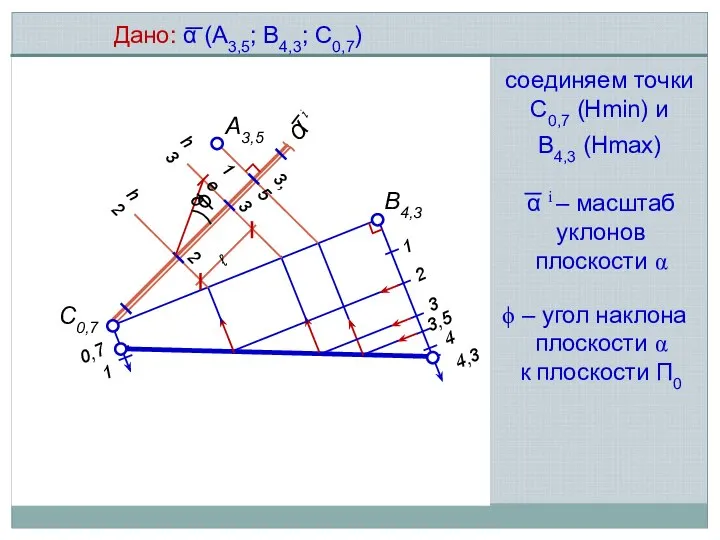
- 5. А3,5 В4,3 С0,7 1 0,7 4,3 1 2 3 3,5 4 3,5 3 2 h2 h3
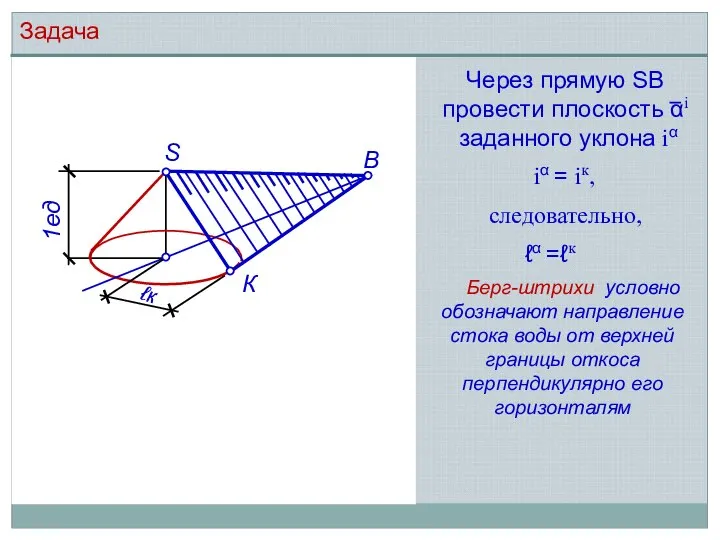
- 6. Задача Через прямую SВ провести плоскость αi заданного уклона iα S В 1ед ℓк К iα
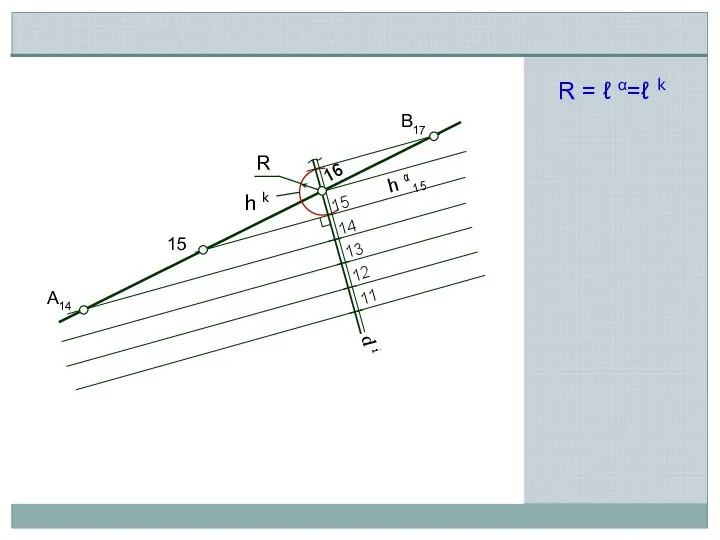
- 7. A14 B17 15 16 14 15 13 12 11 R = ℓ α=ℓ k h k
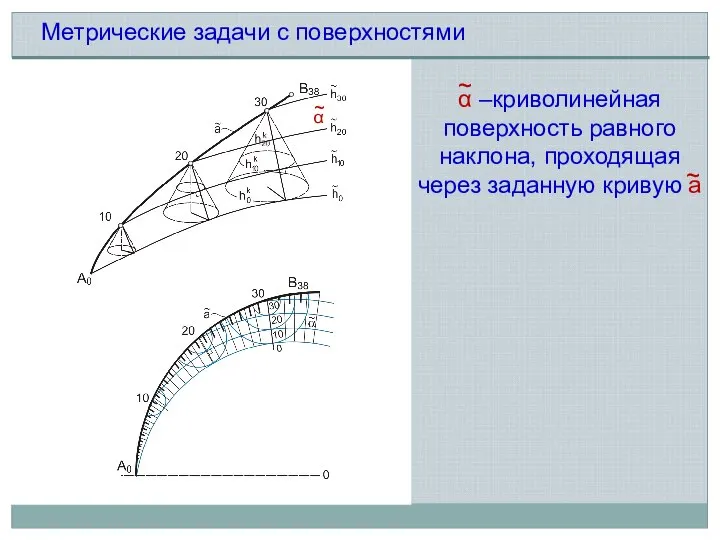
- 8. α –криволинейная поверхность равного наклона, проходящая через заданную кривую а ~ ~ α ~ Метрические задачи
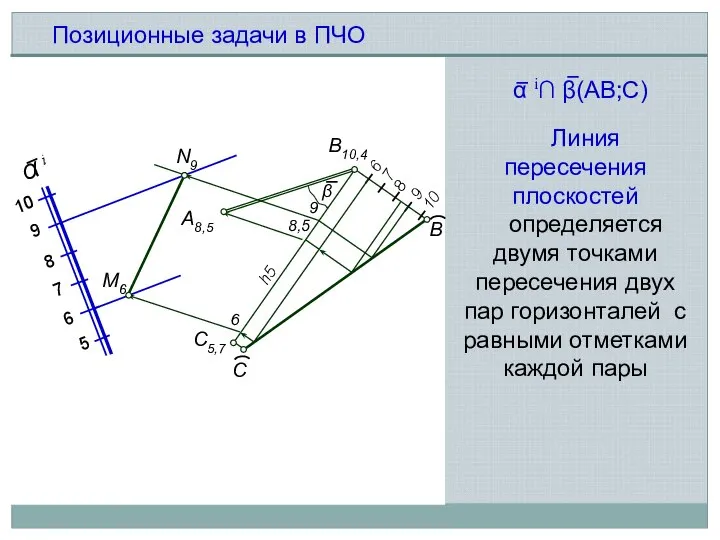
- 9. Позиционные задачи в ПЧО Линия пересечения плоскостей определяется двумя точками пeресечения двух пар горизонталей с равными
- 11. Скачать презентацию
 Возникновение баланса, первые записи о балансе в трактате Л. Пачоли
Возникновение баланса, первые записи о балансе в трактате Л. Пачоли Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Автоматизированная система расчетов ”Onyma”
Автоматизированная система расчетов ”Onyma” Монтаж видео средствами PYTHON (MOVIEPY) и FFMPEG
Монтаж видео средствами PYTHON (MOVIEPY) и FFMPEG 289163
289163 Где обитают знаки препинания?
Где обитают знаки препинания? Weekly Meeting
Weekly Meeting Оборудование для проведения деловых мероприятий
Оборудование для проведения деловых мероприятий Группа компаний Дженерали ППФ в России
Группа компаний Дженерали ППФ в России ЯЗЫКОВОЙ КУРС ПО ВЫБОРУ ДЛЯ 7 КЛАССА «Жизнь в слове и слово в жизни».
ЯЗЫКОВОЙ КУРС ПО ВЫБОРУ ДЛЯ 7 КЛАССА «Жизнь в слове и слово в жизни». Все, что вы хотели знать о сертификации ИТ-специалистов, но боялись спросить
Все, что вы хотели знать о сертификации ИТ-специалистов, но боялись спросить Ата аналар тақтасы
Ата аналар тақтасы Интернет – телевидение (IPTV)
Интернет – телевидение (IPTV) Кредит: зачем он нужен
Кредит: зачем он нужен ПРОЕКТсоздания сети бистрог. Череповец, 2011 год
ПРОЕКТсоздания сети бистрог. Череповец, 2011 год Цемент
Цемент Религия как форма мировоззрения
Религия как форма мировоззрения Кровь как компанент внутренней среды организма
Кровь как компанент внутренней среды организма Психологическая характеристика мышления
Психологическая характеристика мышления Презентация на тему Папство и реформация
Презентация на тему Папство и реформация  «Школьные годы чудесные…»
«Школьные годы чудесные…» Тайны актерского перевоплощения
Тайны актерского перевоплощения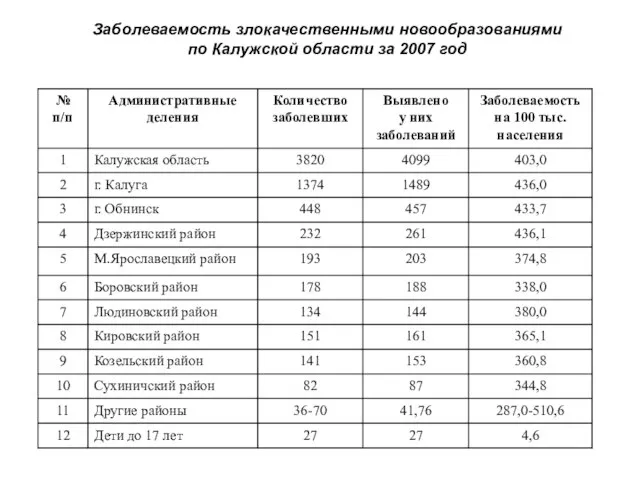 Заболеваемость злокачественными новообразованиями по Калужской области за 2007 год
Заболеваемость злокачественными новообразованиями по Калужской области за 2007 год Наступающий год – год Красной Огненной Свиньи Свинья - последний, 12-й, знак китайского зодиака.
Наступающий год – год Красной Огненной Свиньи Свинья - последний, 12-й, знак китайского зодиака. Цвет в одежде и в жизни
Цвет в одежде и в жизни Цветовой контраст (часть 2)
Цветовой контраст (часть 2) Содержание трудового договора и его существенные условия
Содержание трудового договора и его существенные условия К 65 летию Победы
К 65 летию Победы