Многогранники 3D и 4D: двойственность

Определение многогранника
Многогранником в n-мерном пространстве называется ограниченная замкнутая часть этого пространства, имеющая грани всех размерностей от 0 до n-1.
Пример 1. Трехмерный многогранник имеет грани размерностей 0, 1, 2, которые мы называем вершинами, ребрами и плоскими гранями.
Пример 2. Четырехмерный многогранник имеет грани размерностей 0, 1, 2, 3 – вершины, ребра, грани, плоские грани и трехмерные грани.

Правильный многогранник
Правильным назовем многогранник, грани всех размерностей которого являются также правильными.
Пример 1. У правильного трехмерного многогранника равны между собой все ребра и плоские грани соответственно.
Пример 2. У правильного четырехмерного многогранника равны между собой все ребра, плоские грани и трехмерные грани соответственно.

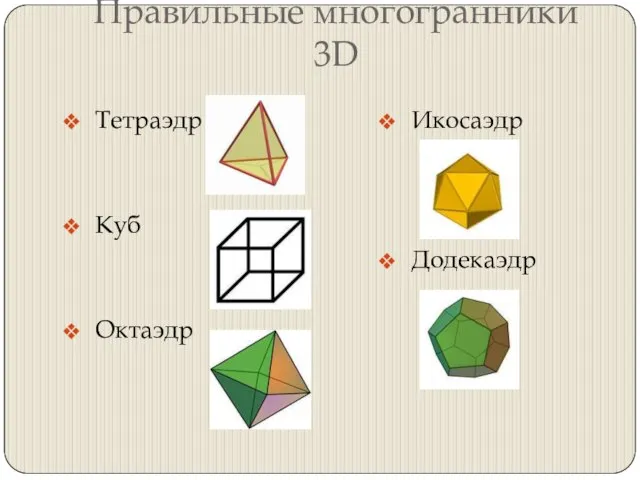
Правильные многогранники 3D
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр

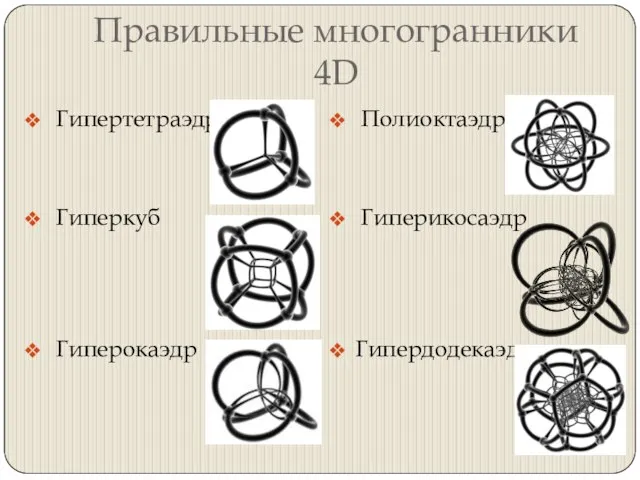
Правильные многогранники 4D
Гипертетраэдр
Гиперкуб
Гиперокаэдр
Полиоктаэдр
Гиперикосаэдр
Гипердодекаэдр

«Звезда» многогранника
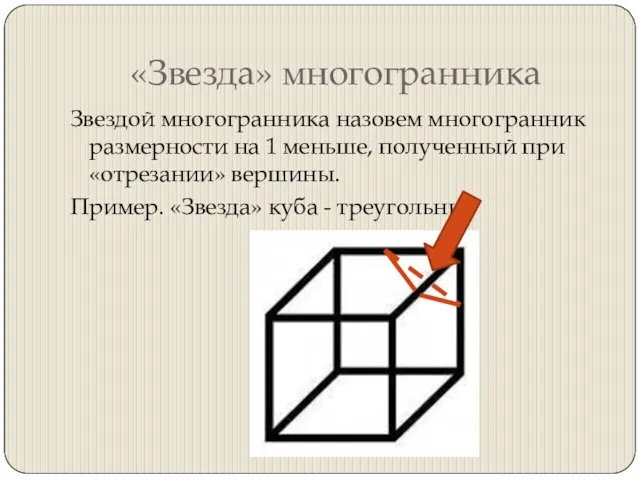
Звездой многогранника назовем многогранник размерности на 1 меньше, полученный при «отрезании» вершины.
Пример. «Звезда» куба - треугольник

Символ Шлефли
Символом Шлефли для правильного многогранника назовем множество { k; m; n;…}, где k – число ребер каждой плоской грани, а остальное множество m; n; … - «звезда» многогранника.
Пример 1. Символ Шлефли для куба {4; 3}
Пример 2. Символ Шлефли для полиоктаэдра {3;4;3}

Таблица взаимосвязи граней(3D)

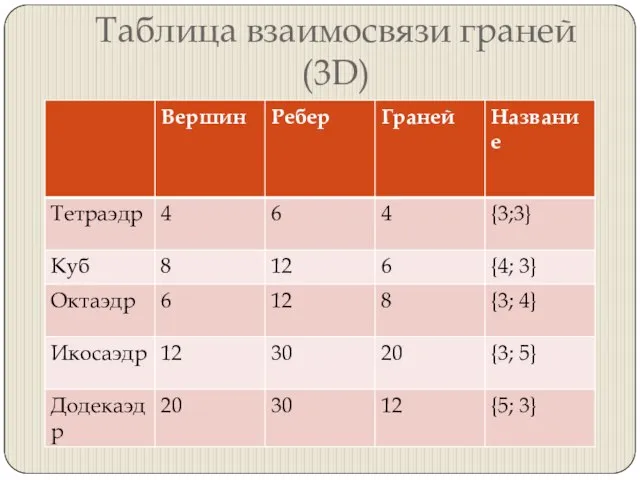
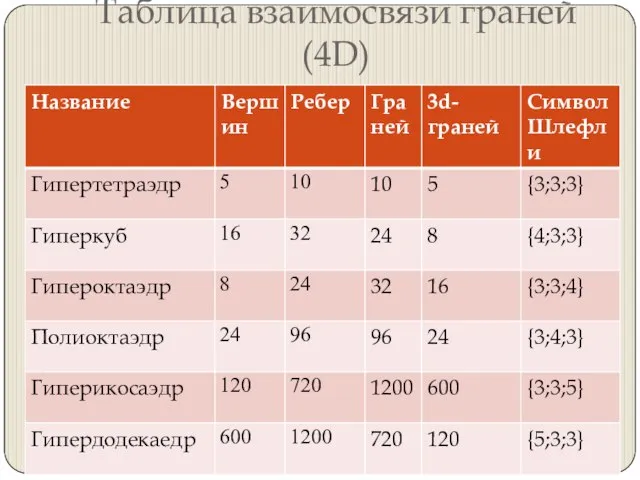
Таблица взаимосвязи граней (4D)

Двойственность
Двойственными назовем многогранники, у которых количество граней всех размерностей расположено в обратном порядке. Иначе говоря, символы Шлефли которых записаны «наоборот»
{4; 3; 3}
{3; 3; 4}

Сделаем выводы о двойственности многогранников:
3D
4D
Тетраэдр – тетраэдр
Куб – Октаэдр
Икосаэдр - Додекаэдр
Гипертетраэдр – гипертетраэдр
Гиперкуб – Гипероктаэдр
Полиоктаэдр – полиоктаэдр
Гиперикосаэдр - гипердодекаэдр

Источники: ссылки на изображения
Тетраэдр http://images.yandex.ru/yandsearch?source=wiz&fp=1&uinfo=ww-1264-wh-625-fw-1023-fh-448-pd-1&p=1&text=%D1%82%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80&noreask=1&pos=54&rpt=simage&lr=2&img_url=http%3A%2F%2Fdiesel.elcat.kg%2Fuploads%2Fmonthly_07_2011%2Fpost-113583-1310311161.jpg
Куб http://images.yandex.ru/yandsearch?text=%D0%BA%D1%83%D0%B1&fp=0&pos=4&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fwww.lapinbook.ru%2Fbook2%2Fmistakes%2Fimg%2F540.jpg
Икосаэдр http://images.yandex.ru/yandsearch?text=%D0%B8%D0%BA%D0%BE%D1%81%D0%B0%D1%8D%D0%B4%D1%80&fp=0&pos=16&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fgraph.power.nstu.ru%2Fwolchin%2Fumm%2FGraphbook%2Fbook%2F001%2F027%2F74%2F74.gif
Додекаэдр http://images.yandex.ru/yandsearch?text=%D0%B4%D0%BE%D0%B4%D0%B5%D0%BA%D0%B0%D1%8D%D0%B4%D1%80&fp=0&pos=3&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2F7%2F73%2FDodecahedron.gif

Источники: ссылки на изображения
Гипертетраэдр http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2Ff%2Ff5%2FStereographic_polytope_5cell.png%2F105px-Stereographic_polytope_5cell.png
Гиперкуб http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F0%2F05%2FStereographic_polytope_8cell.png%2F150px-Stereographic_polytope_8cell.png
Гипероктаэдр http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F2%2F2d%2FStereographic_polytope_16cell.png%2F105px-Stereographic_polytope_16cell.png

Источники: ссылки на изображения
Полиоктаэдр http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F1%2F16%2FStereographic_polytope_24cell.png%2F105px-Stereographic_polytope_24cell.png
Гиперикосаэдр http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F4%2F43%2FStereographic_polytope_600cell.png%2F105px-Stereographic_polytope_600cell.png
Гипердодекаэдр http://images.yandex.ru/yandsearch?text=%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D0%BC%D0%B5%D1%80%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&fp=0&pos=1&uinfo=ww-1264-wh-625-fw-1039-fh-448-pd-1&rpt=simage&img_url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2Fd%2Fdb%2FStereographic_polytope_120cell.png%2F105px-Stereographic_polytope_120cell.png

Источники: печатные
Стрингхем П. Г. Правильные фигуры в n-мерном пространстве. Под ред. Фаге, Успехи математических наук, вып. 10 – М., 1954.
М. Берже, Геометрия, издательство «Мир», 1984 год
М. Бюргер, Сферландия, издательство Амфора, 2001
Пухальская Я. Т. Курсовая работа по теме «Правильный многогранник в n – мерном пространстве». 2006 г.