Многоугольники получающиеся в сечении куба

Цель работы:
Продемонстрировать плоские многоугольники,
которые получаются при сечение
куба плоскостью,
выяснить их вид
и доказать это исходя из основных
теорем и аксиом.

Доказать, что если в сечение куба получится треугольник, то этот треугольник остроугольный.
Задача №1

Построить сечение куба плоскостью, проходящей через концы трех ребер куба, выходящих из одной вершины. Вычислить периметр и площадь сечения, если ребро куба равно а.
Задача №2

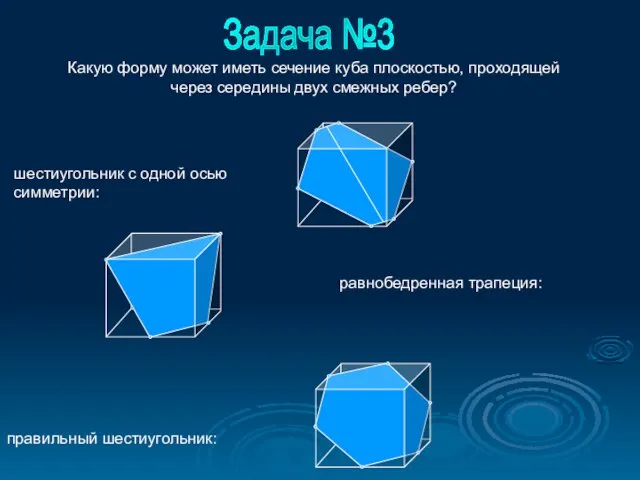
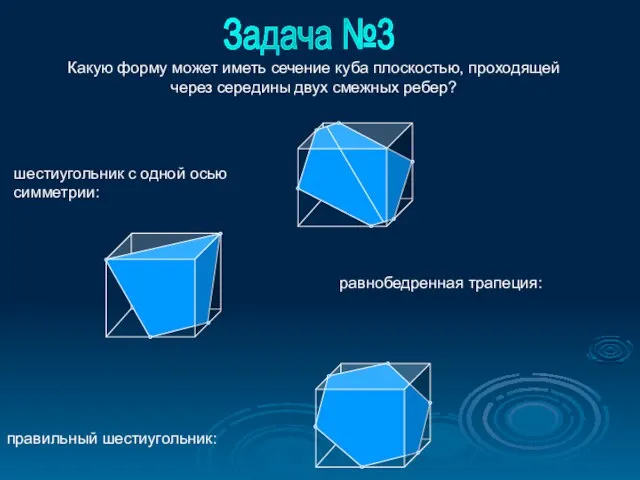
шестиугольник с одной осью симметрии:
правильный шестиугольник:
Задача №3
равнобедренная трапеция:
Какую форму может иметь сечение куба плоскостью, проходящей через середины двух смежных ребер?

Прямоугольник
Диагональ куба выбрана в той диагональной плоскости, которая параллельна прямой МN.
По условию MN параллельна А’С’. Построим MP параллельно DD’ и NL параллельно DD’. Тогда PL параллельно MN. Плоскость MPLN параллельна диагональной плоскости ACC’A’, поскольку проходит через две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости A’C’CA. Диагональ АС’ принадлежит плоскости A’ACC’, значит, AC’ параллельно (PMN).

Трапеция

Пятиугольник с одной осью
Плоскость параллельна диагонали куба, выходящей из общей вершины указанных сторон основания.
Пусть M и N – середины двух смежных сторон грани A’B’C’D’. Отрезки MN и B’D’ пересекаются в точке Р. Проводим отрезок РК параллельно диагоналям BD’. Через две пересекающиеся прямые PK и MN проводим плоскость KLMNT. Она параллельна диагонали BD’.

Правильный шестиугольник

Треугольник
Плоскость параллельна диагонали B’D.
Пусть точка Р – пересечение отрезков B’D’ и MN. В диагональной плоскости BDD’B’ проводим отрезок PQ параллельный диагонали B’D. Искомое сечение представляет собой треугольник MQN.

шестиугольник с одной осью симметрии:
правильный шестиугольник:
Задача №3
равнобедренная трапеция:
Какую форму может иметь сечение куба плоскостью, проходящей через середины двух смежных ребер?