Содержание
- 2. Понятие множества - используют для описания совокупности некоторых предметов или объектов, обладающих определенным набором свойств. Предметы
- 3. 5∈R; -10∈Z; 0,5∉N Виды множеств Конечные - содержат определенное число элементов. Бесконечные - содержат бесконечное число
- 4. Способы задания множеств 1. Перечисление элементов множества M = {2, 3, 5, 7} или M =
- 5. A и B - равны, если они состоят из одних и тех же элементов. ∀x∈ A
- 6. Если в B найдется хотя бы один элемент, не принадлежащий A, то B не будет являться
- 7. Числовые множества - множества, элементами которых являются числа. 1, 2, 3, ..., n, ... образуют множество
- 9. Числовые промежутки a, b ∈ R, a 1. [a, b]={x∈R: a x ∈ [a, b] 2.
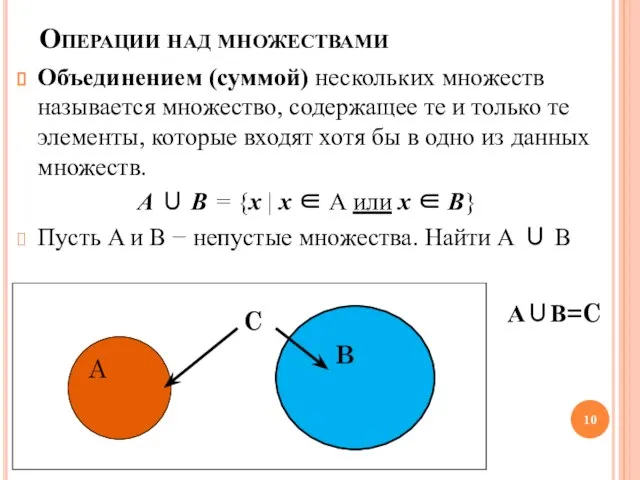
- 10. Операции над множествами Объединением (суммой) нескольких множеств называется множество, содержащее те и только те элементы, которые
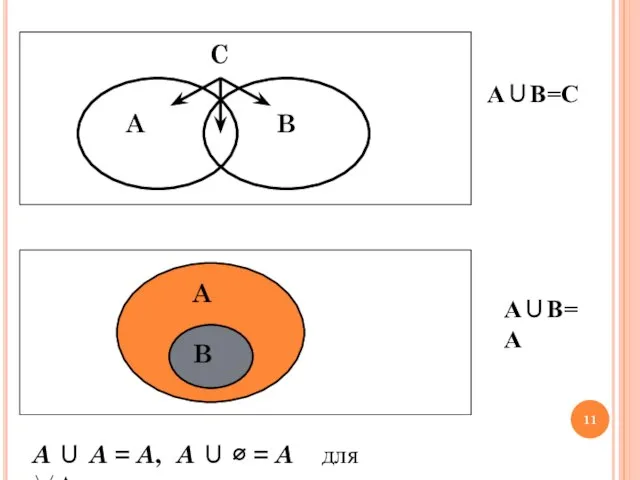
- 11. А∪В=C А∪В=A A ∪ A = A, A ∪ ∅ = A для ∀А
- 12. a). Пусть A = [1; 3], B = [2; 4), найти A ∪ B. A ∪
- 13. b). Пусть A = (−6; 8), B = [0; 3/2], найти A ∪ B. A ∪
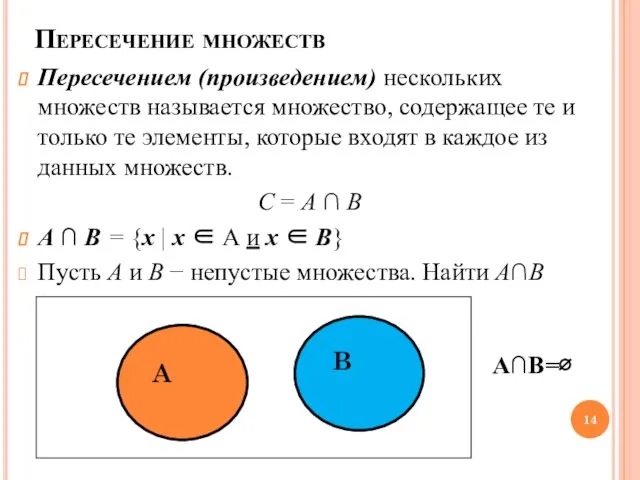
- 14. Пересечение множеств Пересечением (произведением) нескольких множеств называется множество, содержащее те и только те элементы, которые входят
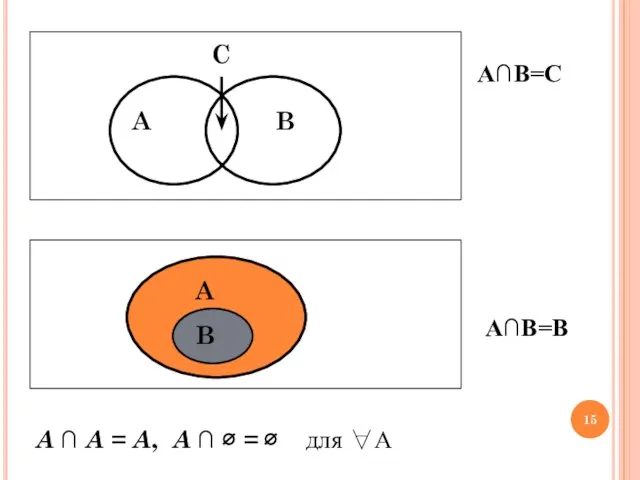
- 15. А∩В=C А∩В=B A ∩ A = A, A ∩ ∅ = ∅ для ∀А
- 16. a). Пусть A = (−∞; −2], B = (−7; 4]. Найти A ∩ B. A ∩
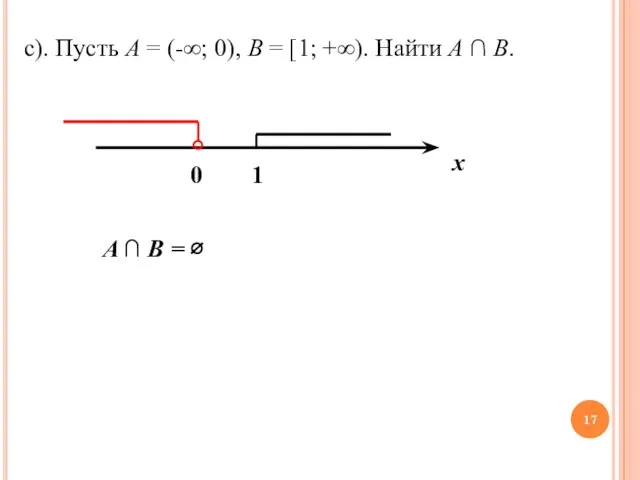
- 17. c). Пусть A = (-∞; 0), B = [1; +∞). Найти A ∩ B. A ∩
- 18. Алгебраические свойства U - универсальное множество, т.е. все рассматриваемые объекты, являются его элементами.
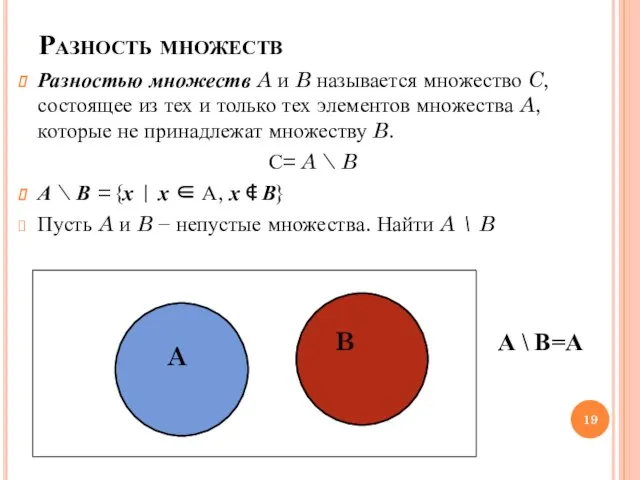
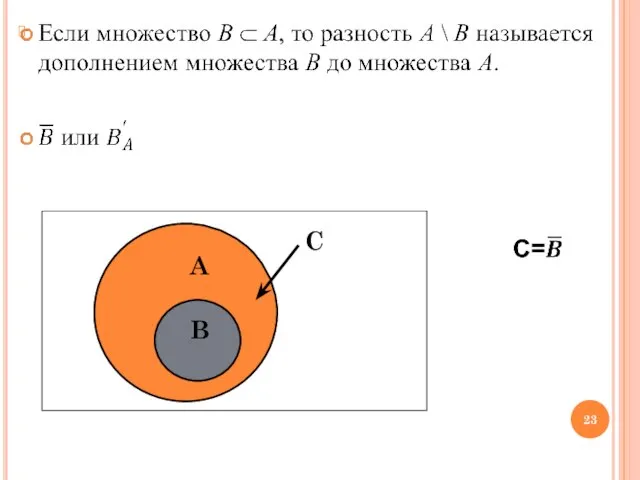
- 19. Разность множеств Разностью множеств A и B называется множество C, состоящее из тех и только тех
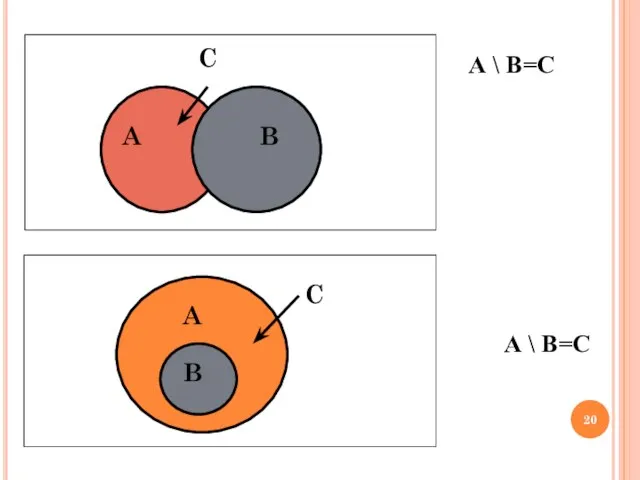
- 20. А \ В=C А \ В=C
- 21. a). Пусть A = (−∞; −2], B = (−7; 4]. Найти A \ B. A \
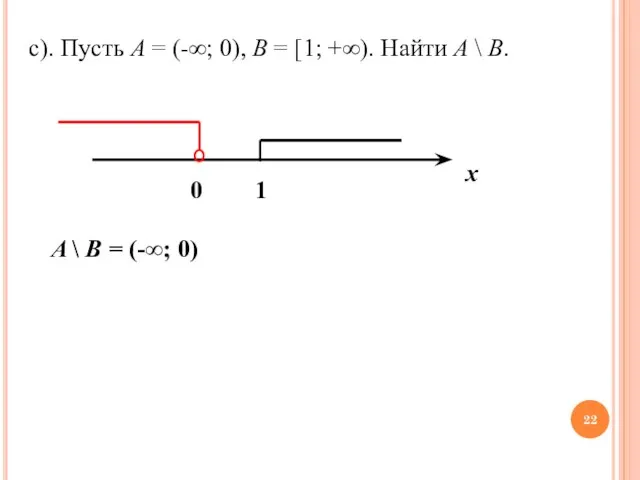
- 22. c). Пусть A = (-∞; 0), B = [1; +∞). Найти A \ B. A \
- 25. Скачать презентацию







![Числовые промежутки a, b ∈ R, a 1. [a, b]={x∈R: a x](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904149/slide-8.jpg)
![a). Пусть A = [1; 3], B = [2; 4), найти A](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904149/slide-11.jpg)
![b). Пусть A = (−6; 8), B = [0; 3/2], найти A](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904149/slide-12.jpg)
![a). Пусть A = (−∞; −2], B = (−7; 4]. Найти A](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904149/slide-15.jpg)

![a). Пусть A = (−∞; −2], B = (−7; 4]. Найти A](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904149/slide-20.jpg)
 По дорогам сказки с музыкой
По дорогам сказки с музыкой Какие бывают деньги (1)
Какие бывают деньги (1) It’s good to be a child
It’s good to be a child Учреждение образования Могилевский государственный областной лицей № 3 Могилев, 2018
Учреждение образования Могилевский государственный областной лицей № 3 Могилев, 2018 Псалом 112, отрока
Псалом 112, отрока Презентация на тему Вязание
Презентация на тему Вязание  ТЕХНОЛОГИЧЕСКИЕ АСПЕКТЫ ПРОВЕДЕНИЯ ГИА-9 ПО ИНОСТРАННЫМ ЯЗЫКАМ
ТЕХНОЛОГИЧЕСКИЕ АСПЕКТЫ ПРОВЕДЕНИЯ ГИА-9 ПО ИНОСТРАННЫМ ЯЗЫКАМ Методы психологического исследования
Методы психологического исследования Биологические ресурсы мира
Биологические ресурсы мира Презентация на тему Автостат
Презентация на тему Автостат  Презентация на тему ПОСТИМПРЕССИОНИЗМ
Презентация на тему ПОСТИМПРЕССИОНИЗМ  СХЕМА НАБЛЮДЕНИЯ ДЛЯ ВЫЯВЛЕНИЯ СФОРМИРОВАННОСТИ РАЗЛИЧНЫХ КОМПОНЕНТОВ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
СХЕМА НАБЛЮДЕНИЯ ДЛЯ ВЫЯВЛЕНИЯ СФОРМИРОВАННОСТИ РАЗЛИЧНЫХ КОМПОНЕНТОВ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ НЕПРОИЗВЕДЕННЫЕ АКТИВЫ (счет 0 103 00 000)
НЕПРОИЗВЕДЕННЫЕ АКТИВЫ (счет 0 103 00 000) Белорусский государственный университет. Филологический факультет
Белорусский государственный университет. Филологический факультет [Предприятие]
[Предприятие] Эмоции человека
Эмоции человека Законодательная база и перспективы развития дополнительного образования на 2020-2030 годы
Законодательная база и перспективы развития дополнительного образования на 2020-2030 годы Презентация на тему A Healthy Way of Life
Презентация на тему A Healthy Way of Life  Алиментарнозависимые заболевания у детей и подростков
Алиментарнозависимые заболевания у детей и подростков сыртқы экономикалық қызметті мемлекеттік басқару осөж номер 2 (1)
сыртқы экономикалық қызметті мемлекеттік басқару осөж номер 2 (1) Алгоритмы
Алгоритмы Художественная вышивка
Художественная вышивка «Күні жетілмеген балалардың күтімі»
«Күні жетілмеген балалардың күтімі» Презентация на тему Общая характеристика Индии
Презентация на тему Общая характеристика Индии  Режим труда и отдыха
Режим труда и отдыха Промышленные подходы привлечения поискового трафика
Промышленные подходы привлечения поискового трафика Орган слуха и равновесия
Орган слуха и равновесия Презентация на тему Социальное развитие и молодежь
Презентация на тему Социальное развитие и молодежь