Моделирование. Решение популяционных задач

Популяция и популяционная динамика
В биологии: популяция - совокупность особей вида, входящая в состав биогеоценоза.
Популяционная динамика, - исследует изменение численности популяции во времени.
Математическое моделирование помогает
формализовать знания об объекте,
дать описание процесса, предсказать его ход и эффективность,
дать рекомендации по управлению этим процессом.
Это крайне важно для биологических процессов, промышленного назначения - биотехнологических систем, продуктивность которых определяется ростом популяций живых организмов.

Популяционная модель неограниченного роста
Модель предложена Т. Мальтусом в 1798 г. в его работе "О росте народонаселения".
Где - численность популяции в году n;
- численность в году n+1;
- коэффициент рождаемости.
Томас Роберт Мальтус (1766-1834) английский демограф и экономист.
Обнаружил, что численность популяций растет в геометрической прогрессии, а производство продуктов питания линейно (в арифметической прогрессии), из чего сделал вывод, что неизбежно наступит мировой голод.

Популяционная модель ограниченного роста
Впервые ограниченный рост популяции, описал Ферхюльст (1848) – в логистическом уравнении.
Это уравнение в дискретном виде
Nn+1=Nn+kNn-qNn2
где Nn+1 численность популяции в году n+1;
Nn - численность популяции в году n;
k – коэффициент рождаемости;
q – коэффициент смертности.

Популяционная модель ограниченного роста
Уравнение ограниченного роста обладает двумя важными свойствами:
при малых х численность х возрастает экспоненциально;
при больших х - приближается к определенному пределу К.
Величина К называется емкость популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования и многими другими факторами, которые могут быть разными для разных видов.
Динамика численности жука Rhizopertha dominica в
10-граммовой порции пшеничных зерен, пополняемых каждую неделю.
Динамика численности жука Rhizopertha dominica

Проверка возможности прогнозирования популяции интерполированием
Используя экспериментальные данные, проверить возможность прогнозирования численности популяции обычными методами интерполяции.
Сделать выводы о возможности применения этих методов в задачах о численности популяции.

Результаты проверки возможности прогнозирования

Вывод:
Методы интерполяции с использованием трендов, имеющиеся в MS Excel, не могут быть использованы для прогнозирования поведения модели ограниченного роста популяции.

Исследование модели популяции

Постановка задачи
Имеется заброшенный пруд, который может быть использован для разведения карпа.
Карпы питаются за счет ресурсов пруда.
Параметры прудового хозяйства определены в рамках математической модели ограниченного роста популяции.

Описание математической модели
Дано:
Nn+1 - численность карпа в году n+1.
Nn - численность карпа в году n.
k=1 – коэффициент рождаемости.
q =0,001 – коэффициент смертности.
Тогда: Nn+1=Nn + k·Nn- q·Nn2
Число карпов на начало года
Родилось карпов за год
погибло карпов
за год
Число карпов к концу года

Математическая модель с учетом ежегодного отлова
Дано:
Nn+1 - численность карпа в году n+1;
Nn - численность карпа в году n;
k=1 – коэффициент рождаемости;
q =0,001 – коэффициент смертности;
U – ежегодный улов, заданный количеством особей
Тогда: Nn+1=Nn+k·Nn-q·Nn2-U
Число карпов на начало года
Родилось карпов за год
погибло карпов
за год
Число карпов к концу года
отловлено карпов за год

Популяция карпа
компьютерная модель в Excel
Размещение исходных данных.

Цель моделирования
Определить емкость популяции.
Определить максимальный годовой улов рыбы, после стабилизации популяции на уровне емкости популяции.
Определить с какого года возможно отлавливать рыбу в максимальном размере.
Определить какое количество элитных мальков карпа надо запустить в пруд, чтобы начать отлов на максимальном уровне уже через год.
Определить через сколько лет окупятся затраты на приобретение элитных мальков. (Кредит 20% годовых)
Исследовать влияние коэффициента рождаемости на динамику популяции, дать своё обоснование каждому из полученных графиков.

Задание
Создать отчет о проведенном исследовании в виде презентации.
1.Слайд «Название и автор».
2.Исследование возможности прогнозирования
3. Слайд «Математическая модель».
4. Слайд «Реализация модели в Excel».
5-11. Слайды ответы на вопросы исследования.
12. Слайд «Направление дальнейших исследований».

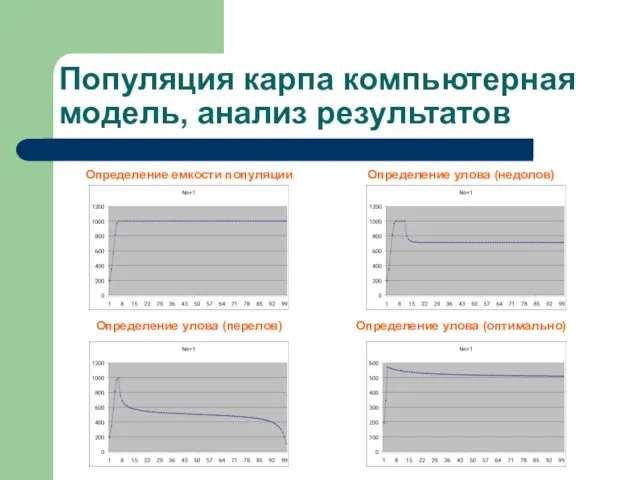
Популяция карпа компьютерная модель, анализ результатов
Определение емкости популяции
Определение улова (недолов)
Определение улова (перелов)
Определение улова (оптимально)

Исследование влияния коэффициента рождаемости

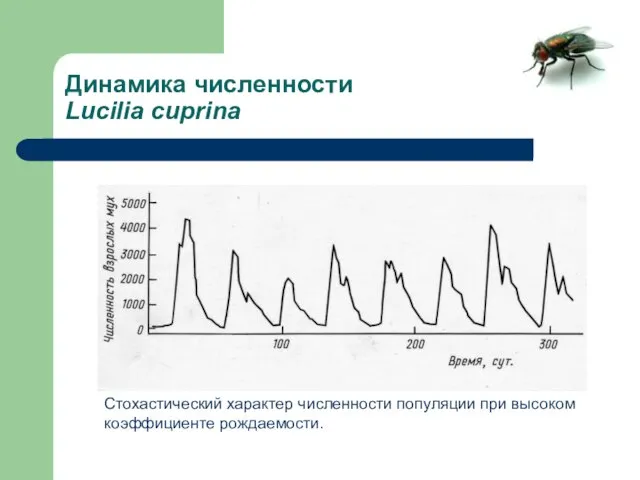
Динамика численности
Lucilia cuprina
Стохастический характер численности популяции при высоком коэффициенте рождаемости.

Список источников информации
Задачник по моделированию «Информатика и ИКТ» 9-11 класс, Макарова Н.В., «Питер», 2008 год.
Избранные вопросы математического моделирования и численных методов. Учебное пособиеИзбранные вопросы математического моделирования и численных методов. Учебное пособие. Автор/создатель: Тарасевич Ю.Ю.,Год: 2004. (http://window.edu.ru/library/pdf2txt/936/38936/16634/page6).
Г.Ю.Ризниченко Популяционная динамика (http://www.library.biophys.msu.ru/MathMod/PD.HTML).
Видео ролик video.raid.ru/pages/video/58845/.
Динамика численности Динамика численности LuciliaДинамика численности Lucilia Динамика численности Lucilia cuprinaДинамика численности Lucilia cuprina Динамика численности Lucilia cuprina http://www.slidefinder.net/l/lect_15_fert_human_pop_growth/32718196/p2.
festival.1september.ru/articles/571753/prez.ppt
kvlar.3dn.ru/dowl/dinamika_populiacii.ppt
http://www.metod-kopilka.ru/page-2-2-9-9.html