Моделирование течения при взлёте и посадке вертолёта

Содержание
Анализ литературы;
Рассмотрение основных положений теории несущего винта вертолёта;
Расчёт внешнего обтекания вертолёта на режиме взлёта и посадки (снижения).
Рассмотрение проблемы обтекания заокнцовок лопастей;
Постановка задачи.
2/41
Д.Г. Ковытин
2018

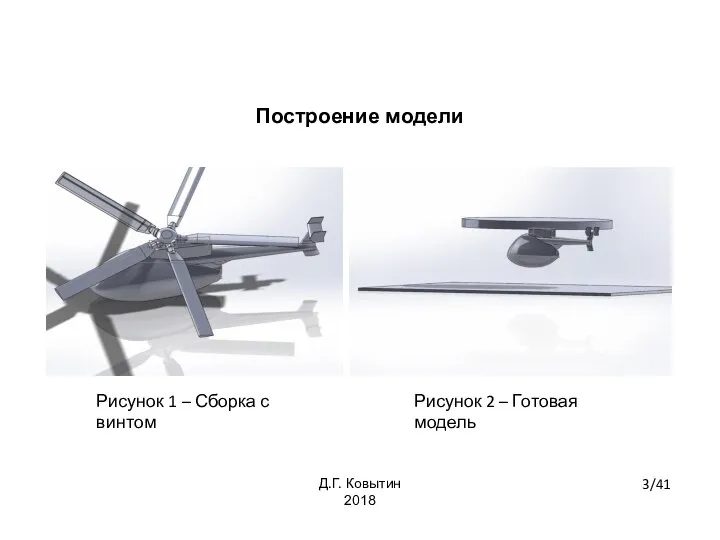
Построение модели
Рисунок 1 – Сборка с винтом
Рисунок 2 – Готовая модель
3/41
Д.Г. Ковытин
2018

Построение сетки для взлёта
Сначала настраивается базовая сетка, затем, на основе базовой строится итоговая сетка
Итоговая сетка для взлёта насчитывает 2205313 ячеек.
Рисунок 3 – Базовая сетка
Рисунок 4 – Итоговая сетка
4/41
Д.Г. Ковытин
2018

Построение сетки для посадки
Финальная сетка для посадки насчитывает примерно 3000000 ячеек
Рисунок 5 – Базовая сетка
Рисунок 6 – Итоговая сетка
5/41
Д.Г. Ковытин
2018

Математическая модель и настройка решателя
Flow simulation моделирует движение потока, на основе решения осреднённых по Рейнольдсу уравнений Навье−Стокса. Жидкость принята несжимаемой.
Исходные уравнения Навье−Стокса:
6/41
Д.Г. Ковытин
2018

Диссипативная функция
Уравнение состояния
Тензор вязких напряжений
Вязкость
7/41
Д.Г. Ковытин
2018

В SolidWorks используется модель турбулентности k-e standart. Благодаря быстрой сходимости и относительно низким требованиям к объему памяти k-ε модель очень популярна при решении задач.
Внутренняя энергия
Плотность теплового потока
8/41
Д.Г. Ковытин
2018
,где

Осреднение по Рейнольдсу и Фавру
Метод осреднения по Рейнольдсу заключается в замене случайных значений параметра на сумму средних и пульсационных значении этого же параметра.
9/41
Для сжимаемых течений часто используют осреднение по Фавру:
Д.Г. Ковытин
2018

Осреднённые уравнения
Применив осреднения по Рейнольдсу и по Фавру получим:
10/41
Д.Г. Ковытин
2018

Гипотеза Буссинеска:
Осреднённые уравнения, с учётом этой гипотезы:
11/41
Д.Г. Ковытин
2018

В данной модели решается 2 дополнительных уравнения для транспорта кинетической энергии турбулентности (k) и транспорта диссипации турбулентности (ε).
12/41
Д.Г. Ковытин
2018

Исходные данные
Нормальная взлётная масса: 1 361 [кг];
Угол установки лопастей: 11 [град] при взлёте, 9,7 [град] при спуске ;
Скорость подъёма(спуска): 6 [м/с], 4 [м/с] (начальное условие)
Подключено условие на стенке;
Задана область вращения;
Скорость вращения винта: 220 [об/мин] на подъёме, 200 [об/мин] при спуске;
Профиль лопасти: NACA 0015 (рисунок 7).
Рисунок 7
13/41
Д.Г. Ковытин
2018

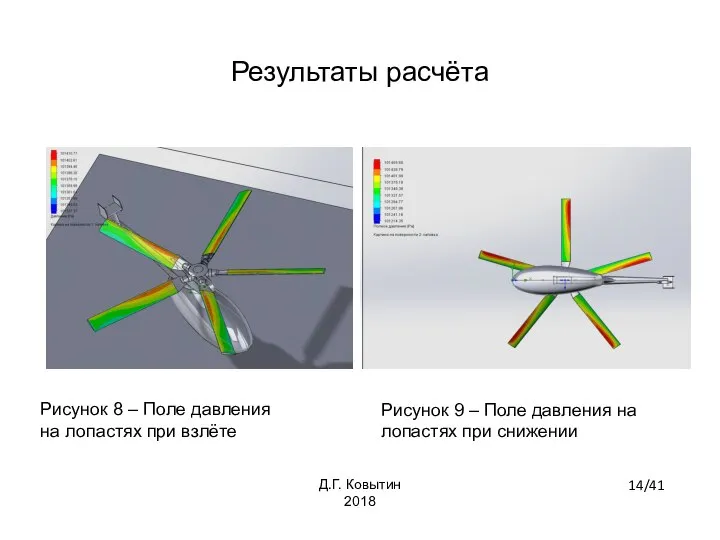
Результаты расчёта
Рисунок 8 – Поле давления
на лопастях при взлёте
Рисунок 9 – Поле давления на
лопастях при снижении
14/41
Д.Г. Ковытин
2018

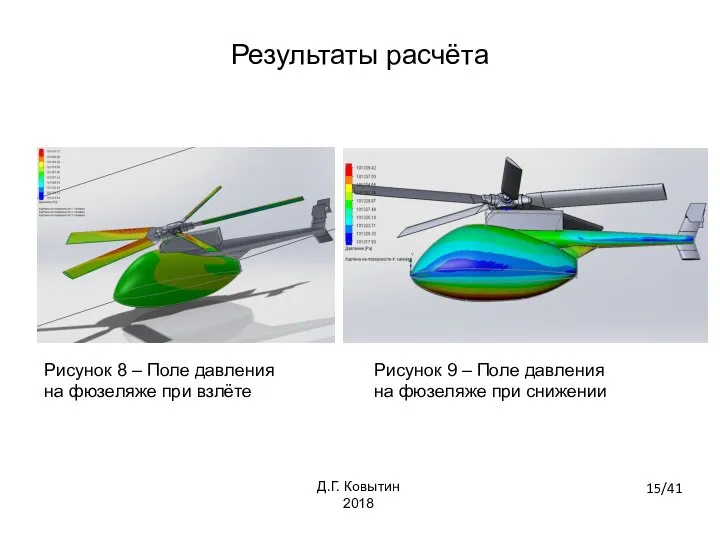
Рисунок 8 – Поле давления
на фюзеляже при взлёте
Рисунок 9 – Поле давления
на фюзеляже при снижении
15/41
Д.Г. Ковытин
2018
Результаты расчёта

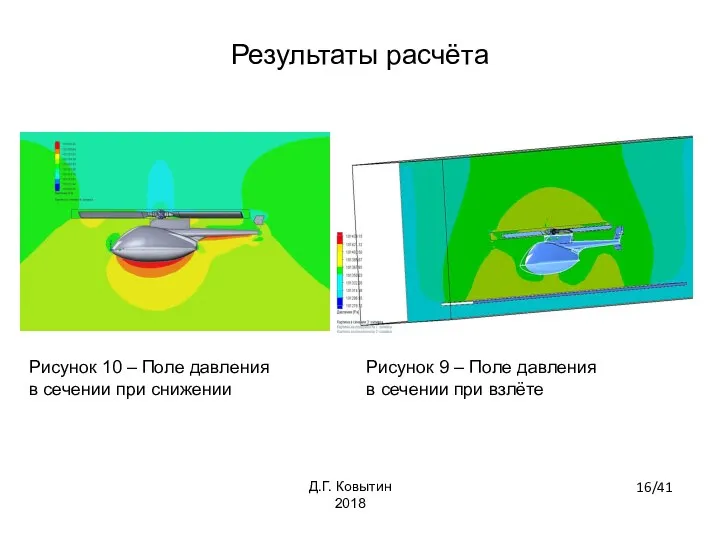
Рисунок 10 – Поле давления
в сечении при снижении
Рисунок 9 – Поле давления
в сечении при взлёте
16/41
Д.Г. Ковытин
2018
Результаты расчёта

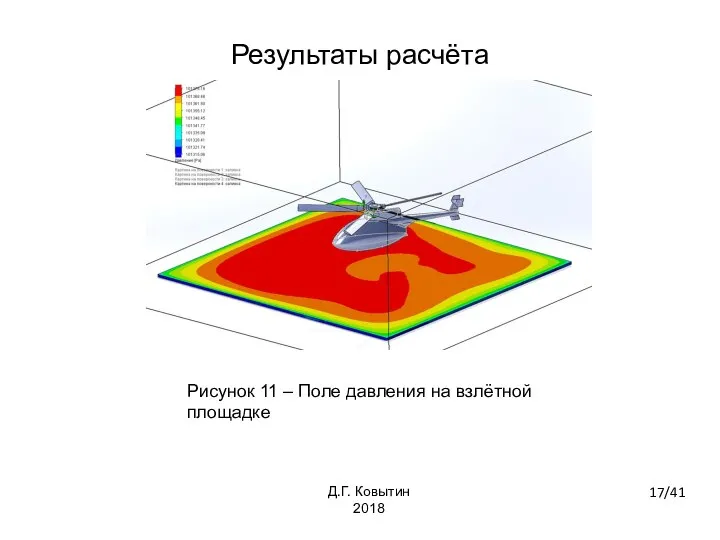
Рисунок 11 – Поле давления на взлётной площадке
17/41
Д.Г. Ковытин
2018
Результаты расчёта

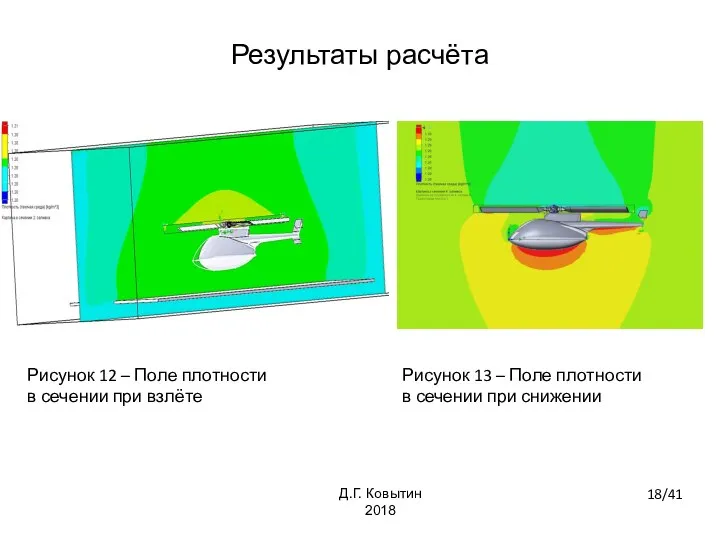
Рисунок 12 – Поле плотности
в сечении при взлёте
Рисунок 13 – Поле плотности
в сечении при снижении
18/41
Д.Г. Ковытин
2018
Результаты расчёта

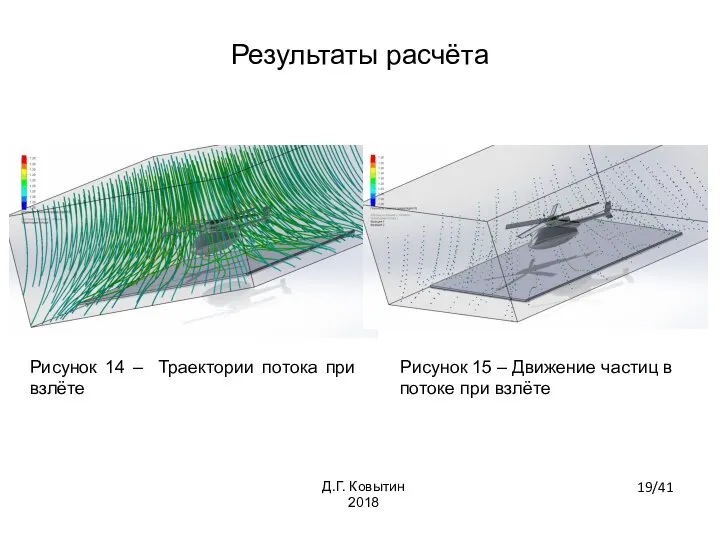
Рисунок 14 – Траектории потока при взлёте
Рисунок 15 – Движение частиц в потоке при взлёте
19/41
Д.Г. Ковытин
2018
Результаты расчёта

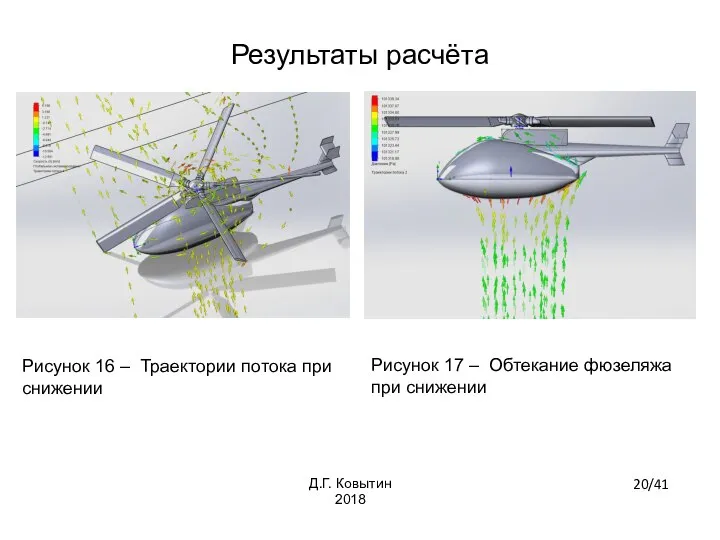
Рисунок 16 – Траектории потока при снижении
Рисунок 17 – Обтекание фюзеляжа при снижении
20/41
Д.Г. Ковытин
2018
Результаты расчёта

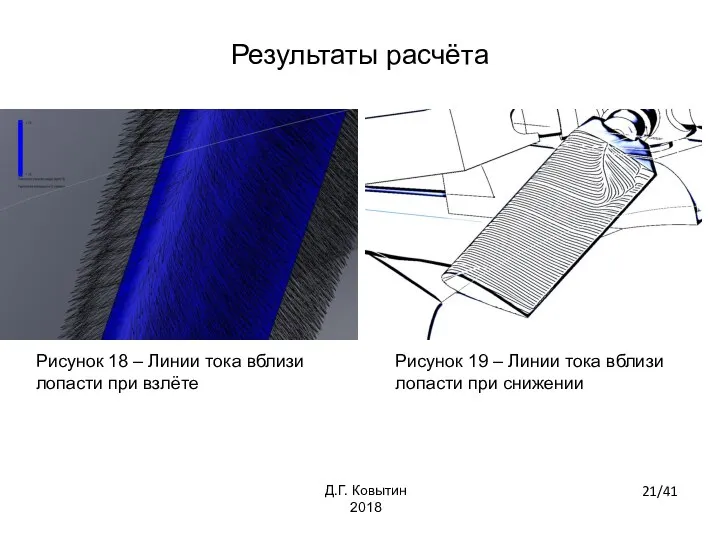
Рисунок 18 – Линии тока вблизи лопасти при взлёте
Рисунок 19 – Линии тока вблизи лопасти при снижении
21/41
Д.Г. Ковытин
2018
Результаты расчёта

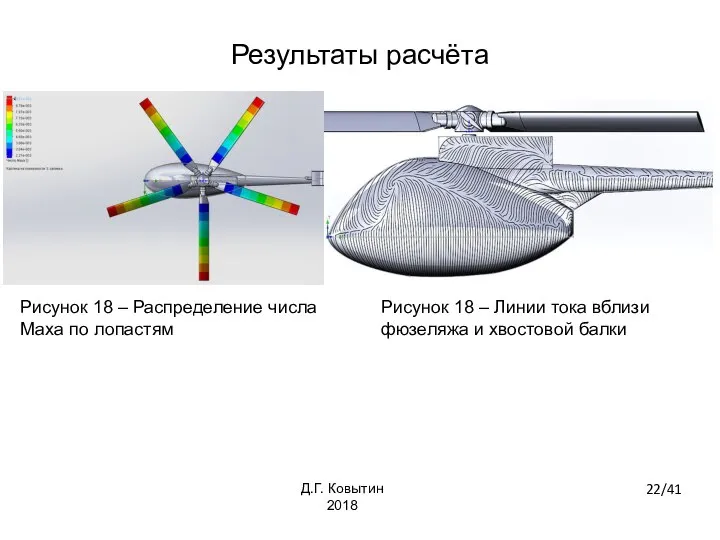
Рисунок 18 – Линии тока вблизи фюзеляжа и хвостовой балки
Рисунок 18 – Распределение числа Маха по лопастям
22/41
Д.Г. Ковытин
2018
Результаты расчёта

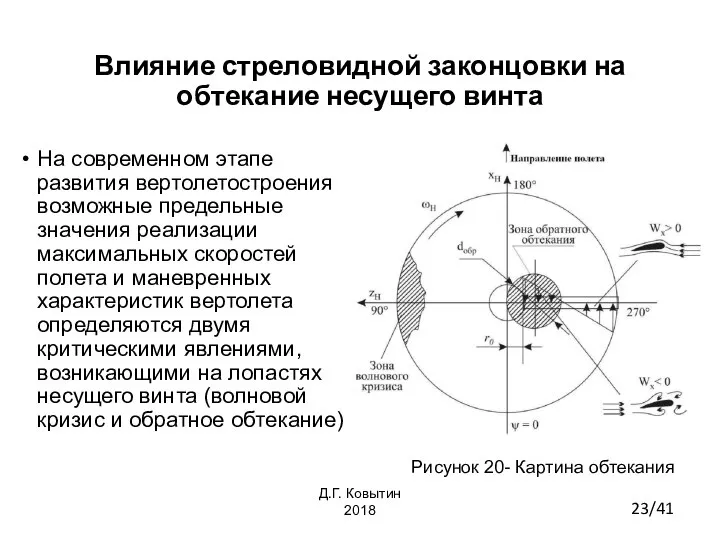
Влияние стреловидной законцовки на обтекание несущего винта
На современном этапе развития вертолетостроения возможные предельные значения реализации максимальных скоростей полета и маневренных характеристик вертолета определяются двумя критическими явлениями, возникающими на лопастях несущего винта (волновой кризис и обратное обтекание)
Рисунок 20- Картина обтекания
23/41
Д.Г. Ковытин
2018

Способы борьбы с критическими явлениями
использование специальных профилей с большим значением критического числа Маха (Мкр ≥ 0.95) и благоприятным изменением моментных характеристик профиля на трансзвуковых скоростях;
применение различных видов аэродинамических профилей переменной относительной толщины по длине лопасти (профилировка лопасти);
установка специальных законцовок лопастей НВ, позволяющих уменьшить величину Мкр наступающей лопасти, улучшить влияние концевого вихря лопасти на аэродинамические характеристики несущего винта.
24/41
Д.Г. Ковытин
2018

Виды законцовок
Рисунки 21,22- Виды законцовок
25/41
Д.Г. Ковытин
2018

Способы борьбы с критическими явлениями
26/41
Д.Г. Ковытин
2018

Способы борьбы с критическими явлениями
У современных вертолетов окружная скорость конца лопасти достигает величины wR =220…230 м/с, что соответствует числам М наступающей лопасти при максимальных скоростях полета M =1.05…0.95.
При проектировании современного скоростного вертолета необходимо обеспечить компромиссное решение при выборе частоты вращения винта: с одной стороны – уменьшение числа М конца наступающей лопасти позволяет ослабить проявление эффектов сжимаемости воздуха; с другой стороны – увеличение окружной скорости конца лопасти приводит к уменьшению зоны срыва и обратного обтекания на диске несущего винта.
27/41
Д.Г. Ковытин
2018

Принятые допущения
Лопасть является абсолютно жесткой на изгиб и кручение ;
Не учтена нестационарность обтекания сечений лопасти, т. е. использована гипотеза стационарности при определении аэродинамических характеристик профилей;
Аэродинамические характеристики профилей сечений лопасти не зависят от угла скольжения потока вдоль лопасти и влияния центробежных сил на пограничный слой;
Не учтена жесткость проводки управления.
28/41
Д.Г. Ковытин
2018

Постановка задачи
29/41
Д.Г. Ковытин
2018

Постановка задачи
Расчёты аэродинамических характеристик профиля и моделей крыльев выполнялись Ю.М. Игнаткиным, С.Г. Константиновым на суперкомпьютере МАИ ( Электронный журнал «Труды МАИ». Выпуск № 57 ) в CFD пакете ANSYS FLUENT , в котором для описания движения вязкого турбулентного потока сжимаемого газа используются осредненные по Рейнольдсу уравнения Навье-Стокса .
Для подтверждения достоверности полученных результатов расчётов они сравнивались с результатами экспериментов, полученных в дозвуковой аэродинамической трубе НК МАИ и в сверхзвуковой - Т-2 МАИ
30/41
Д.Г. Ковытин
2018

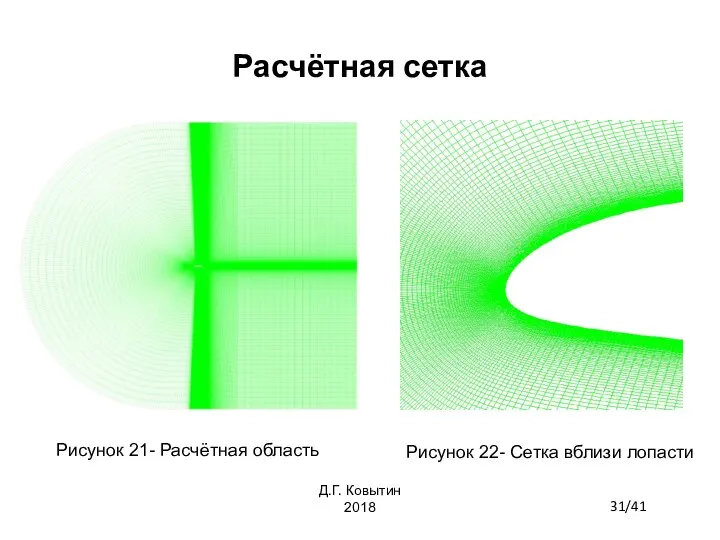
Расчётная сетка
Рисунок 21- Расчётная область
Рисунок 22- Сетка вблизи лопасти
31/41
Д.Г. Ковытин
2018

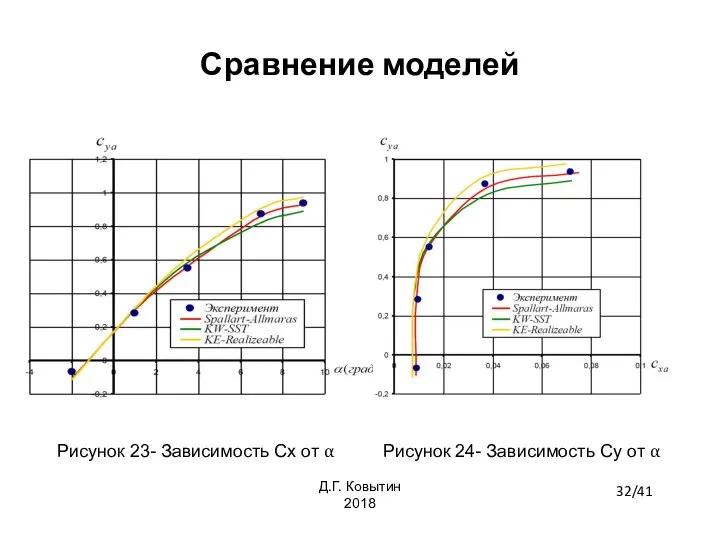
Сравнение моделей
Рисунок 23- Зависимость Cx от α
Рисунок 24- Зависимость Cy от α
32/41
Д.Г. Ковытин
2018

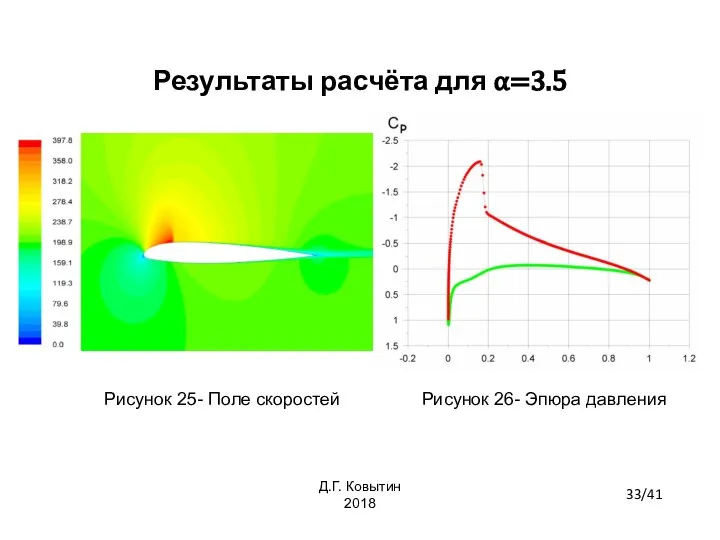
Результаты расчёта для α=3.5
Рисунок 25- Поле скоростей
Рисунок 26- Эпюра давления
33/41
Д.Г. Ковытин
2018

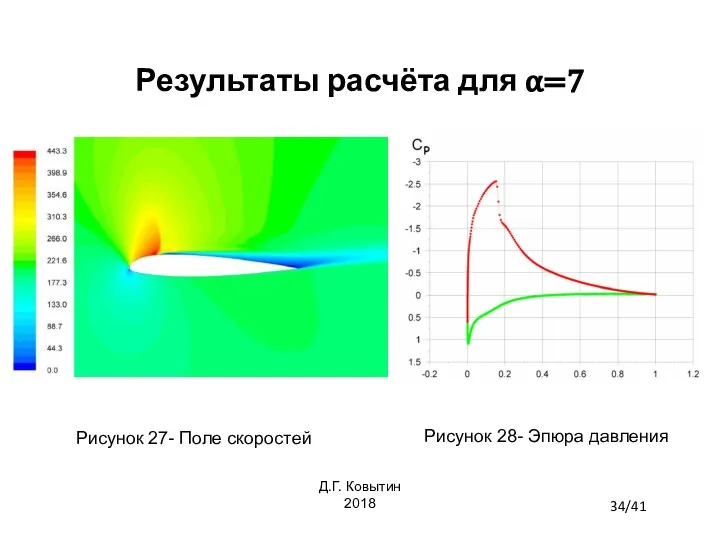
Результаты расчёта для α=7
Рисунок 27- Поле скоростей
Рисунок 28- Эпюра давления
34/41
Д.Г. Ковытин
2018

Использованные законцовки
35/41
Д.Г. Ковытин
2018

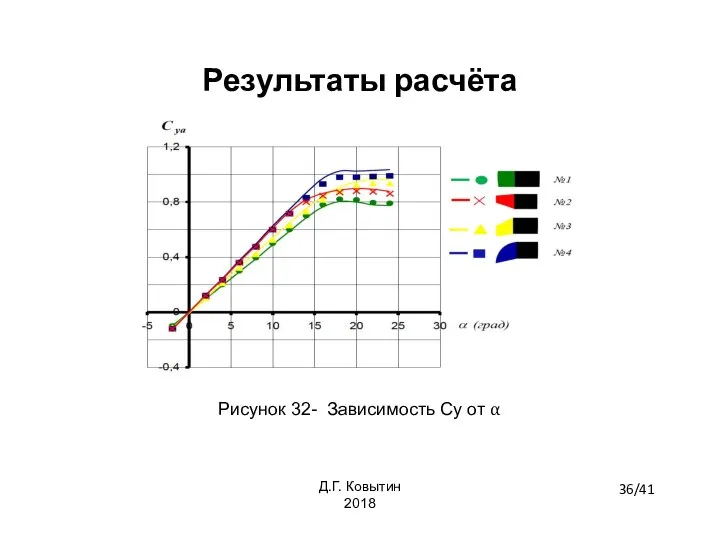
Результаты расчёта
Рисунок 32- Зависимость Сy от α
36/41
Д.Г. Ковытин
2018

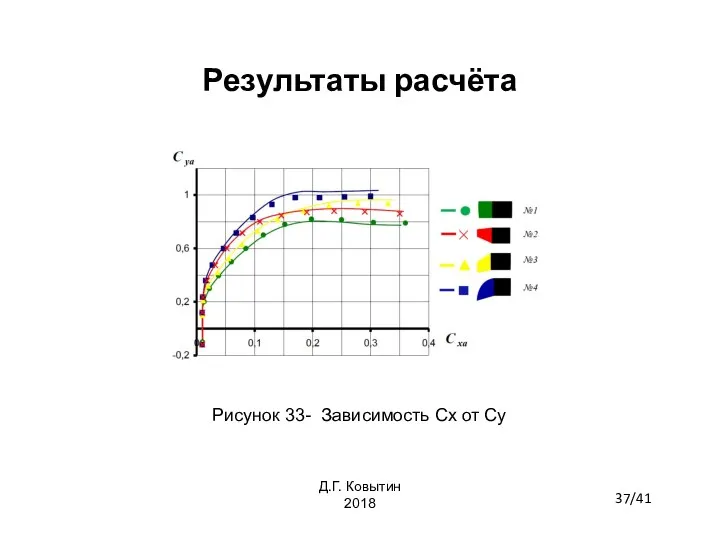
Результаты расчёта
Рисунок 33- Зависимость Сx от Су
37/41
Д.Г. Ковытин
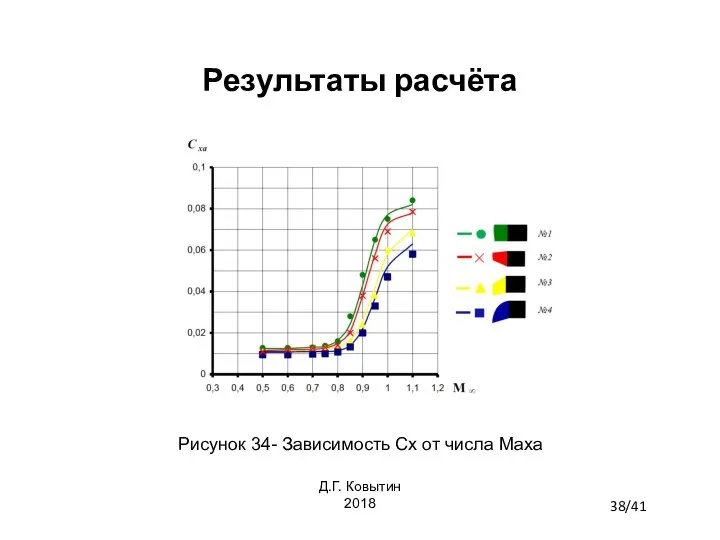
2018

Результаты расчёта
Рисунок 34- Зависимость Сх от числа Маха
38/41
Д.Г. Ковытин
2018

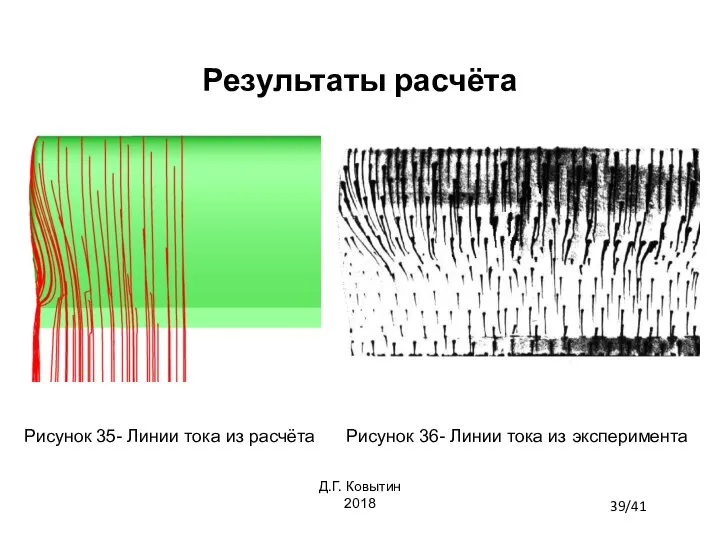
Результаты расчёта
Рисунок 35- Линии тока из расчёта
Рисунок 36- Линии тока из эксперимента
39/41
Д.Г. Ковытин
2018

Выводы
Построена 3-D модель гражданского вертолёта Hughes 500E и выполнен расчёт обтекания фюзеляжа и несущего винта вблизи поверхности на режимах взлета и посадки;
Обтекание несущего винта моделировалось на основе упрощенной теории несущего винта; обтекание фюзеляжа моделировалось численно на основе уравнений Рейнольдса с k−ε моделью турбулентности в пакете SolidWorks 16.0;
Получены и проанализированы картины обтекания вертолёта и поля газодинамических параметров в потоке, на фюзеляже и лопастях винта;
Проанализированы результаты расчёта МАИ для выбранных форм законцовок.
Д.Г. Ковытин
2018
40/41