Содержание
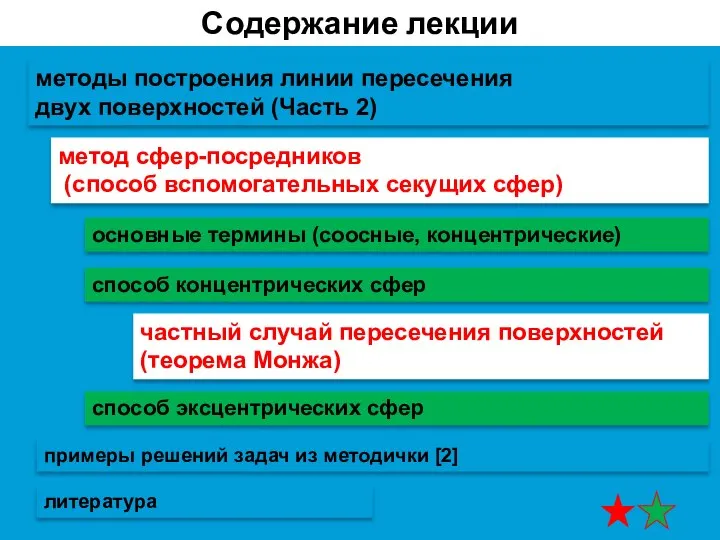
- 2. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) метод сфер-посредников (способ вспомогательных секущих сфер)
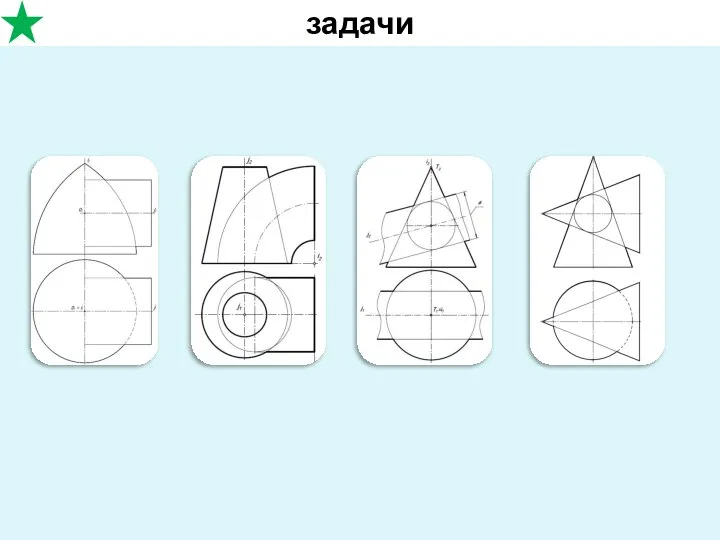
- 3. задачи
- 4. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
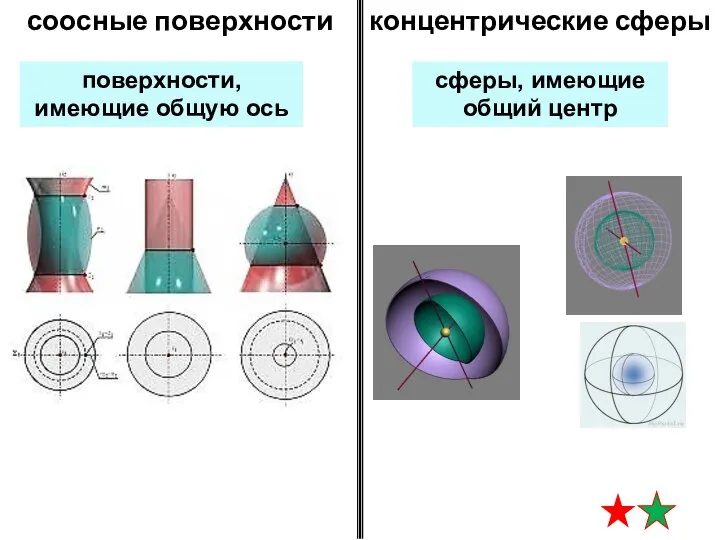
- 5. сферы, имеющие общий центр концентрические сферы соосные поверхности поверхности, имеющие общую ось
- 6. способ вспомогательных секущих сфер если центр сферы лежит на оси какой-либо поверхности вращения, то сфера соосна
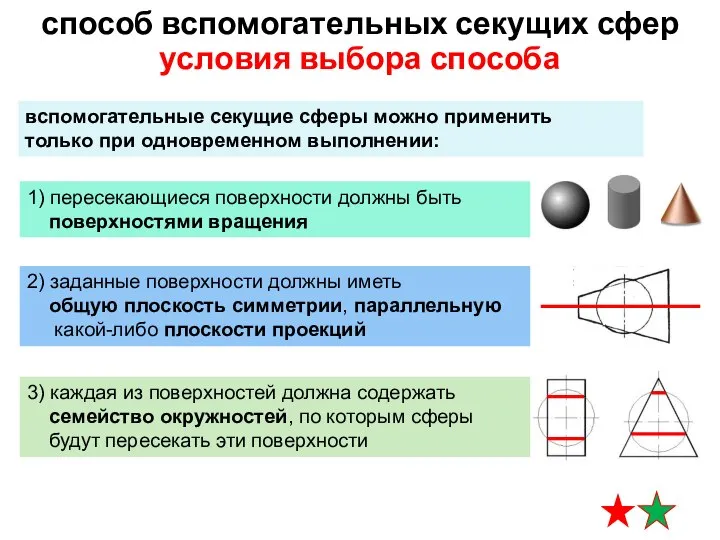
- 7. вспомогательные секущие сферы можно применить только при одновременном выполнении: условия выбора способа способ вспомогательных секущих сфер
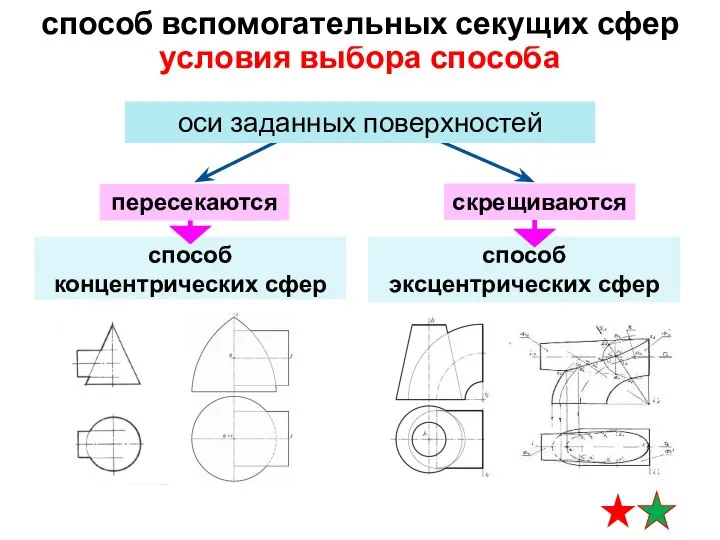
- 8. способ эксцентрических сфер способ концентрических сфер условия выбора способа способ вспомогательных секущих сфер пересекаются скрещиваются оси
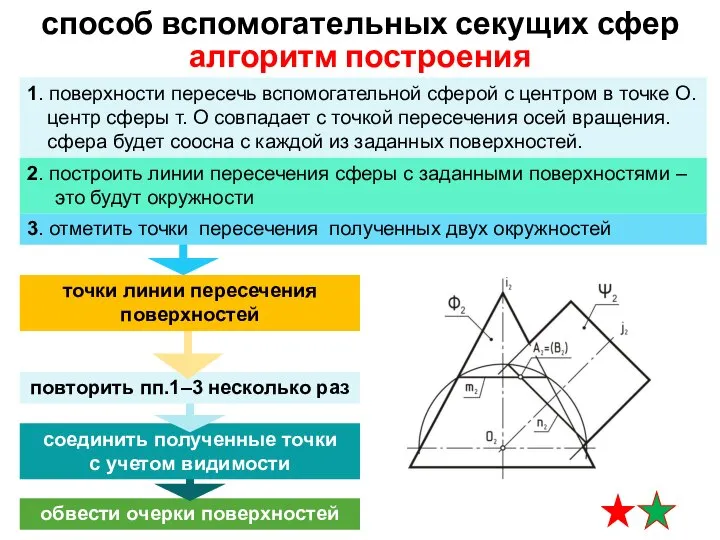
- 9. обвести очерки поверхностей соединить полученные точки с учетом видимости повторить пп.1–3 несколько раз алгоритм построения способ
- 10. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
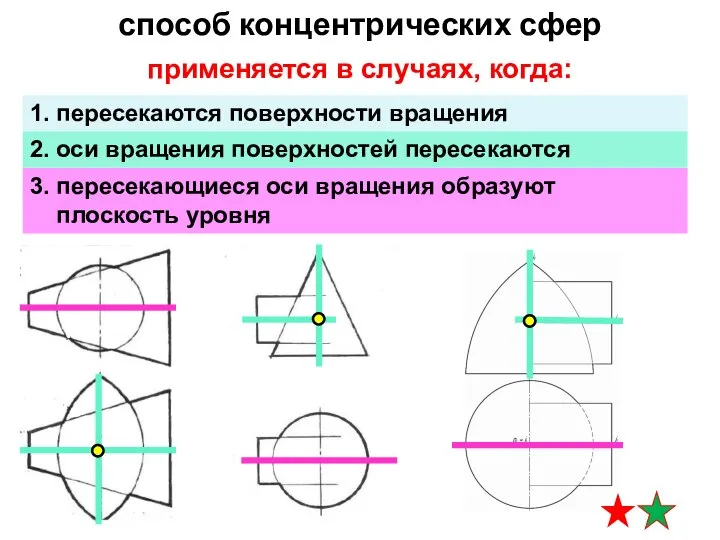
- 11. способ концентрических сфер 1. пересекаются поверхности вращения 2. оси вращения поверхностей пересекаются 3. пересекающиеся оси вращения
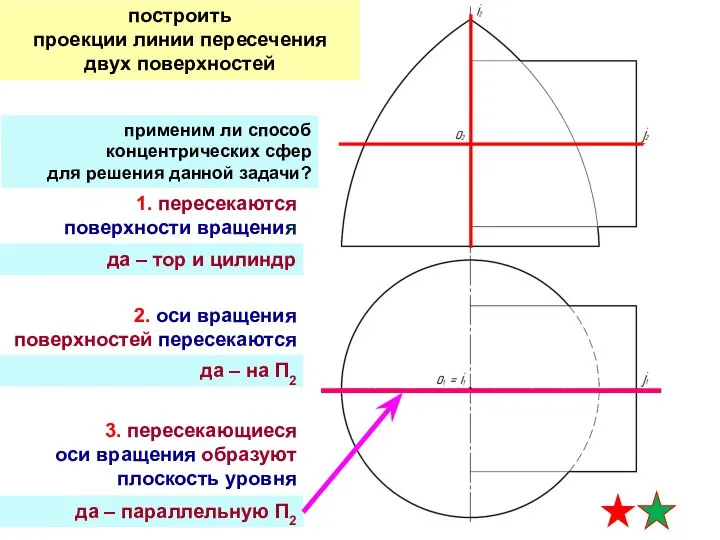
- 12. применим ли способ концентрических сфер для решения данной задачи? 1. пересекаются поверхности вращения 2. оси вращения
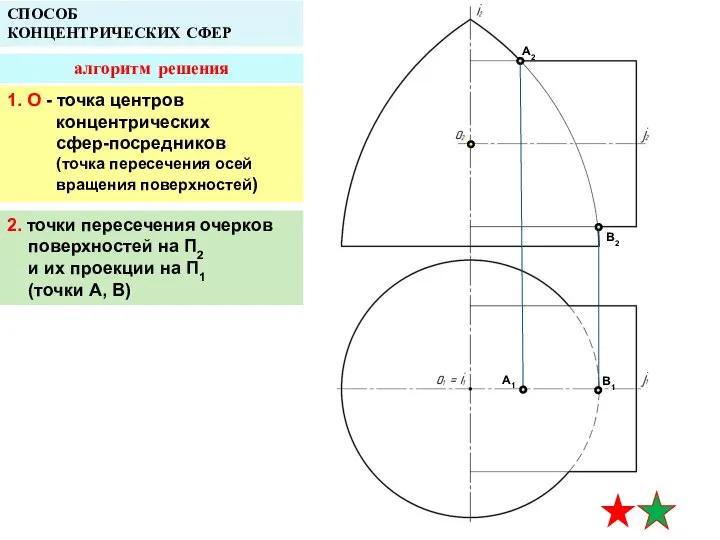
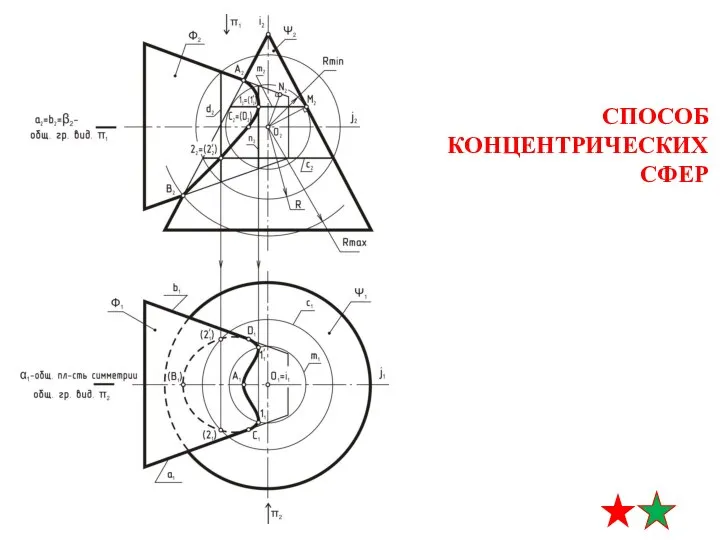
- 13. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 1. О - точка центров концентрических сфер-посредников (точка пересечения осей вращения
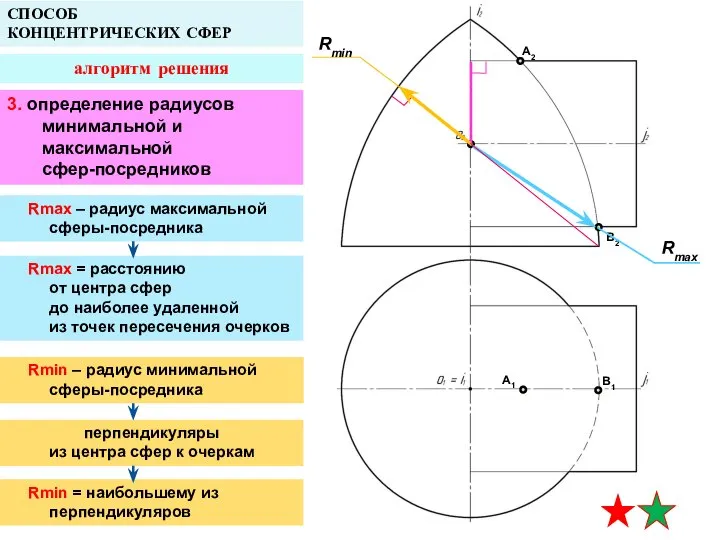
- 14. A2 B2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 3. определение радиусов минимальной и максимальной сфер-посредников
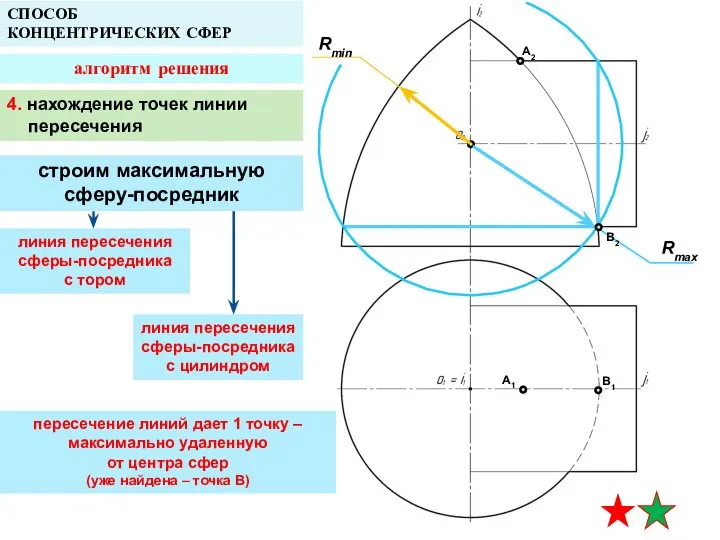
- 15. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmax Rmin 4. нахождение точек линии пересечения строим
- 16. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 4. нахождение точек линии пересечения строим
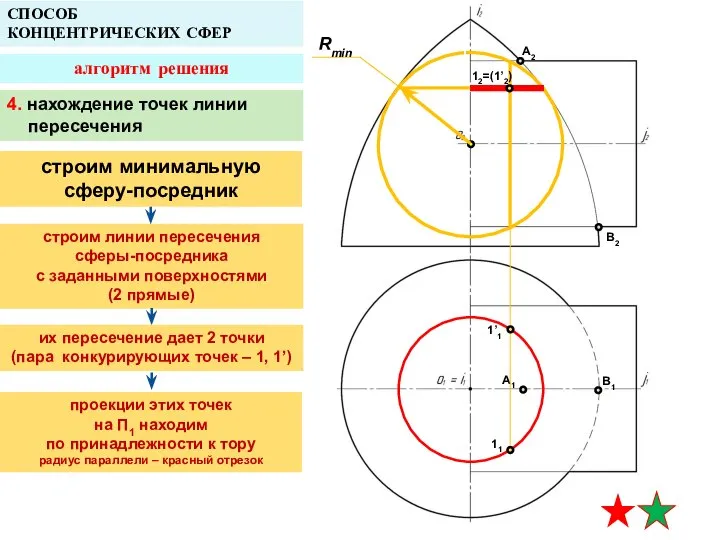
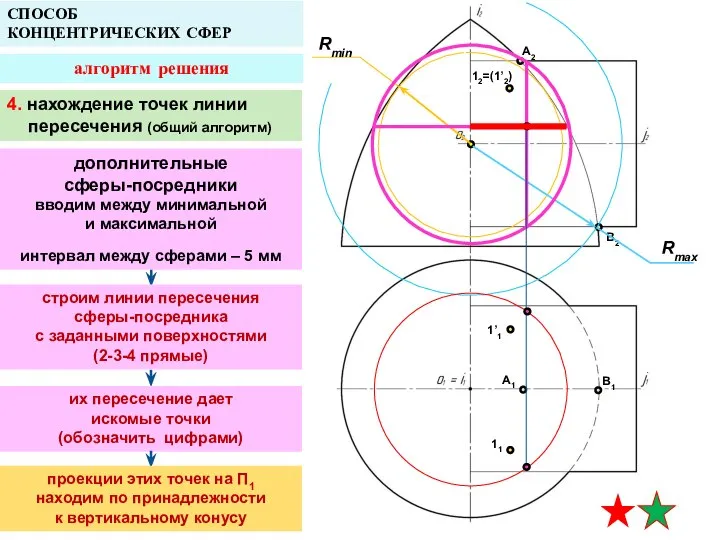
- 17. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
- 18. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
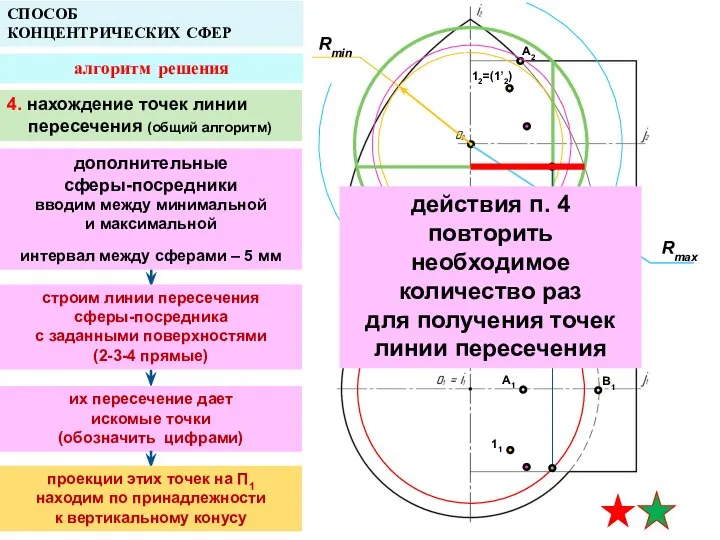
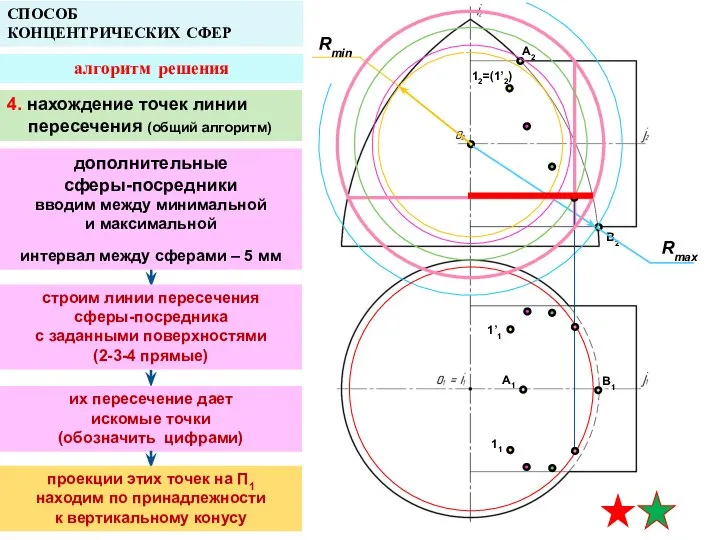
- 19. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
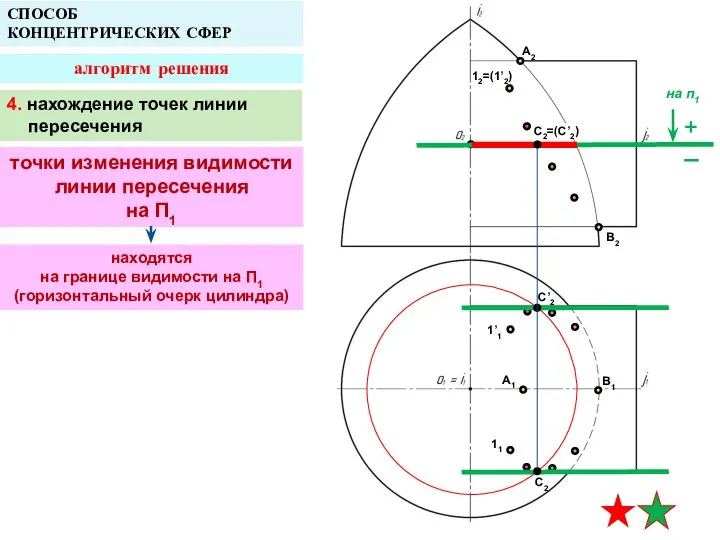
- 20. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 находятся на границе видимости
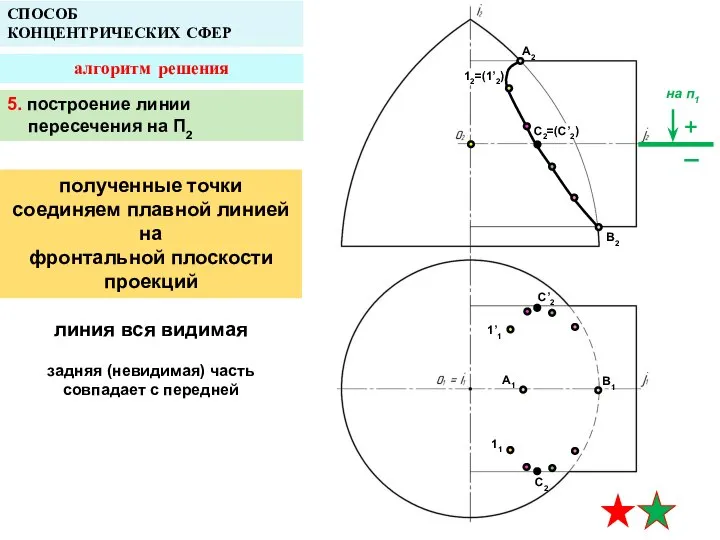
- 21. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 5.
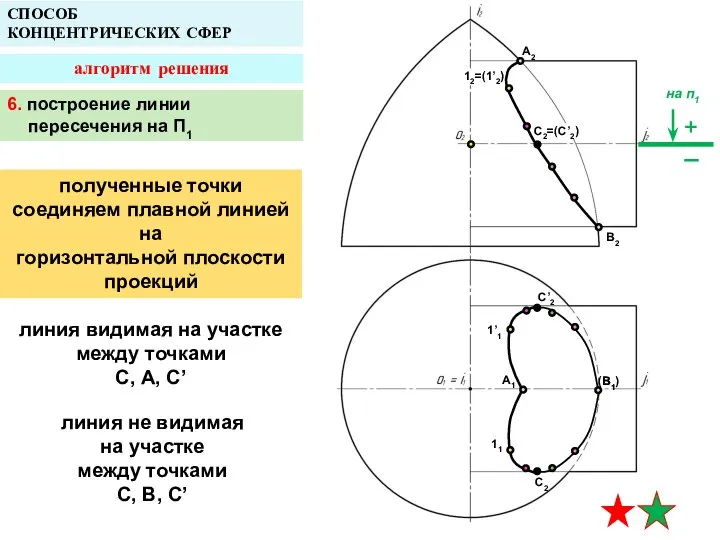
- 22. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 6.
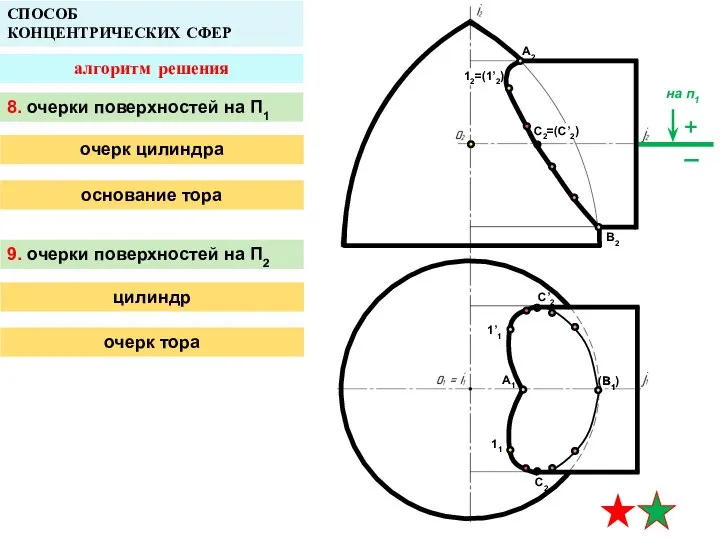
- 23. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 (B1)
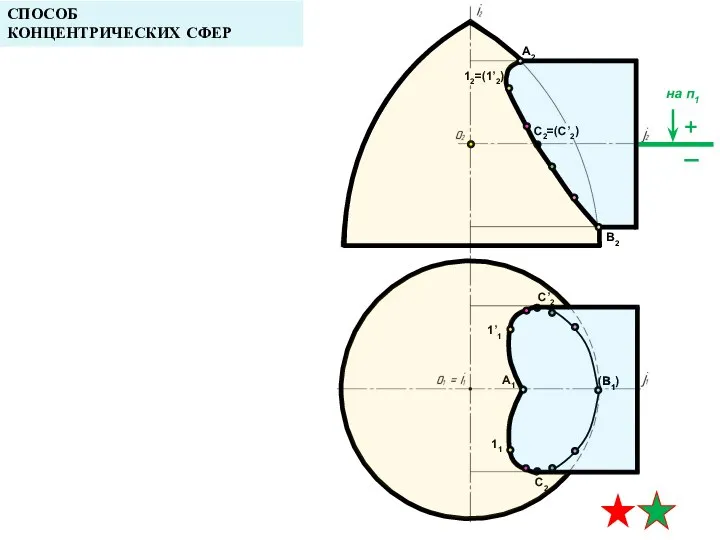
- 24. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 (B1)
- 25. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
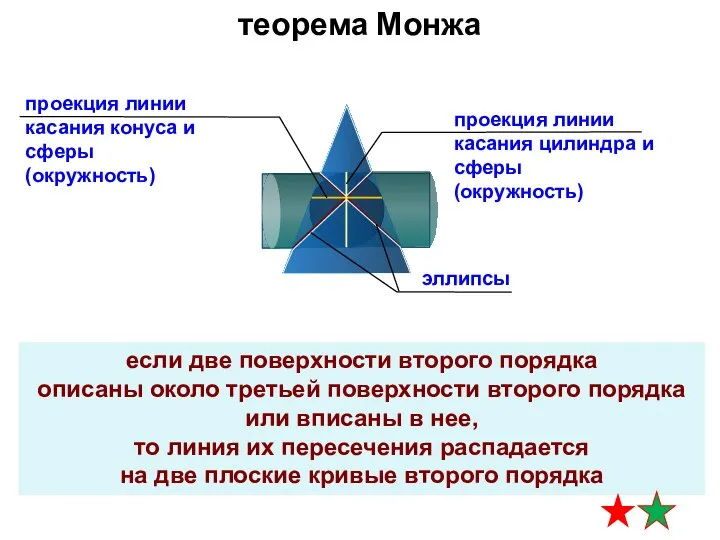
- 26. если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то
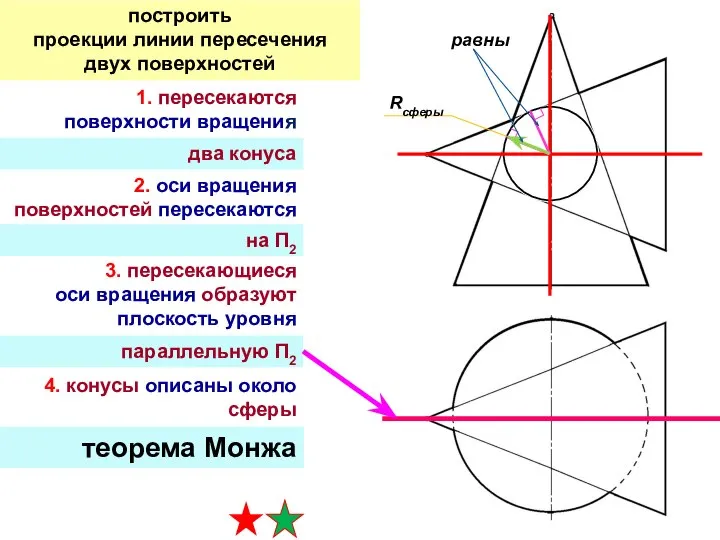
- 27. 1. пересекаются поверхности вращения 2. оси вращения поверхностей пересекаются 3. пересекающиеся оси вращения образуют плоскость уровня
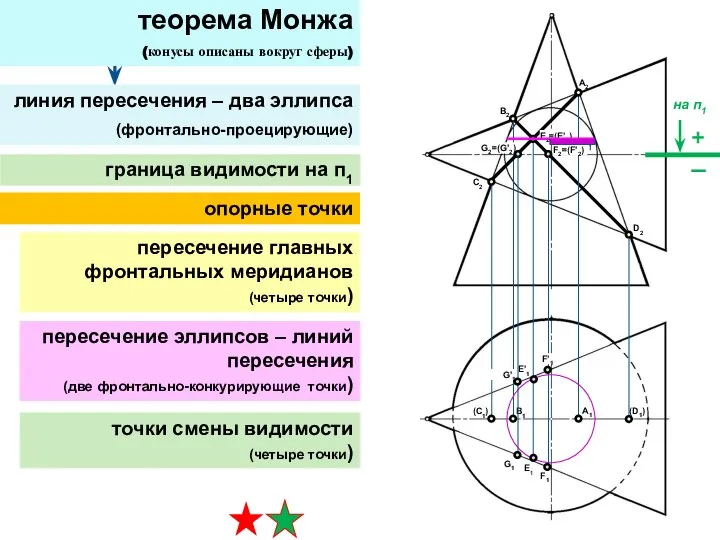
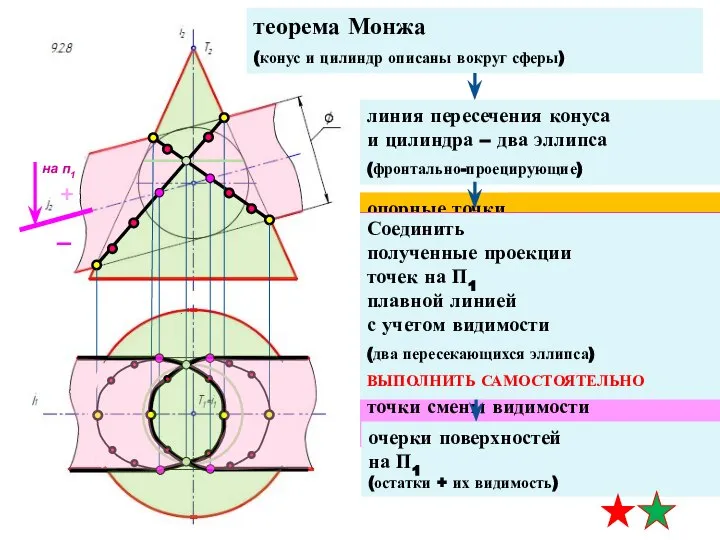
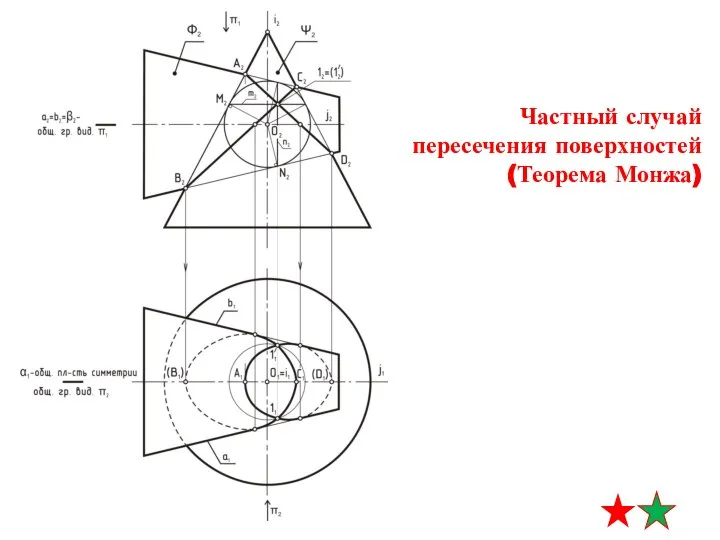
- 28. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) опорные точки пересечение главных
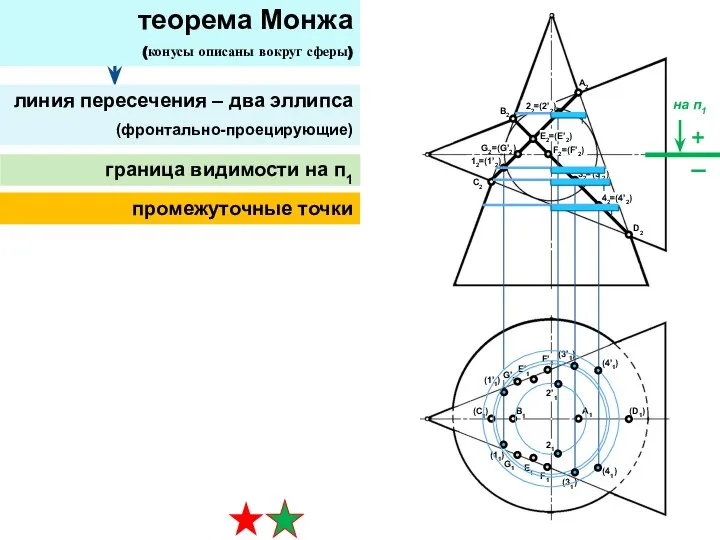
- 29. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) промежуточные точки граница видимости
- 30. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) граница видимости на п1
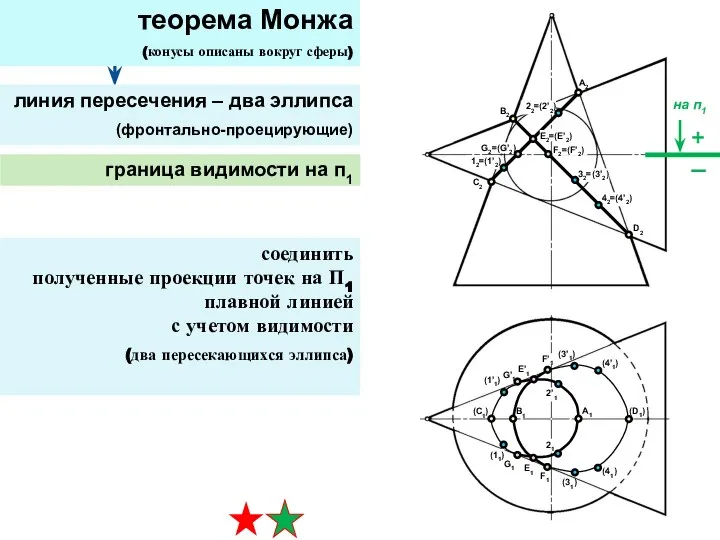
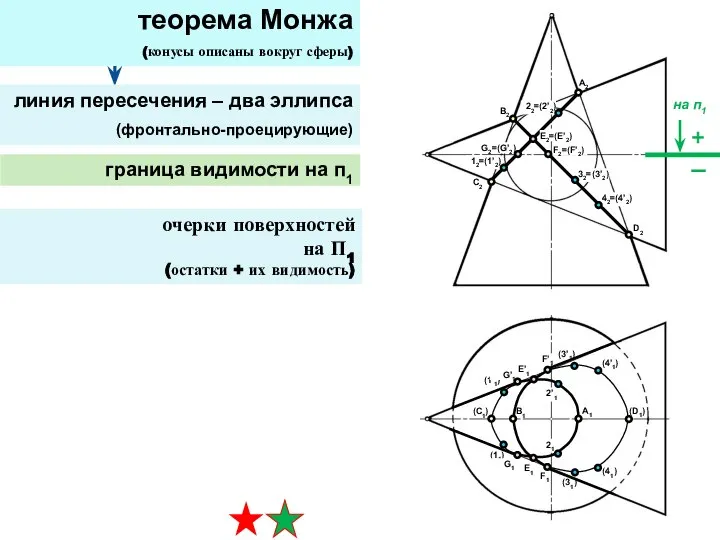
- 31. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) граница видимости на п1
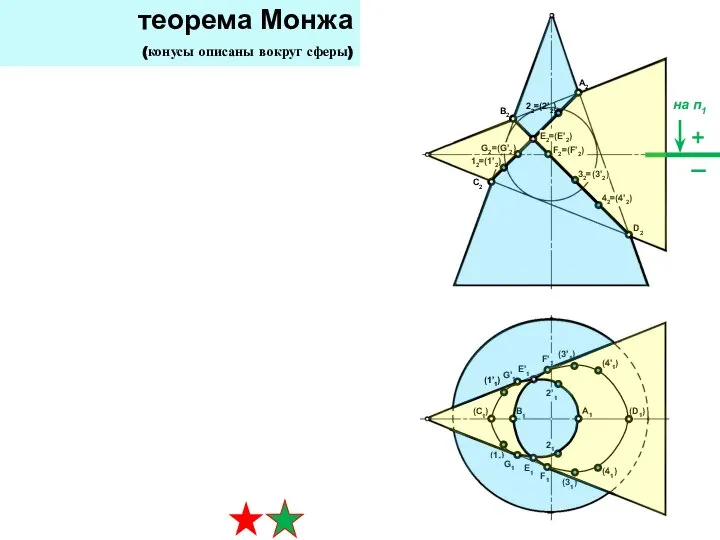
- 32. теорема Монжа (конусы описаны вокруг сферы)
- 33. построить на П1 по принадлежности к конусу (САМОСТОЯТЕЛЬНО) пересечение главных фронтальных меридианов (четыре точки) теорема Монжа
- 34. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
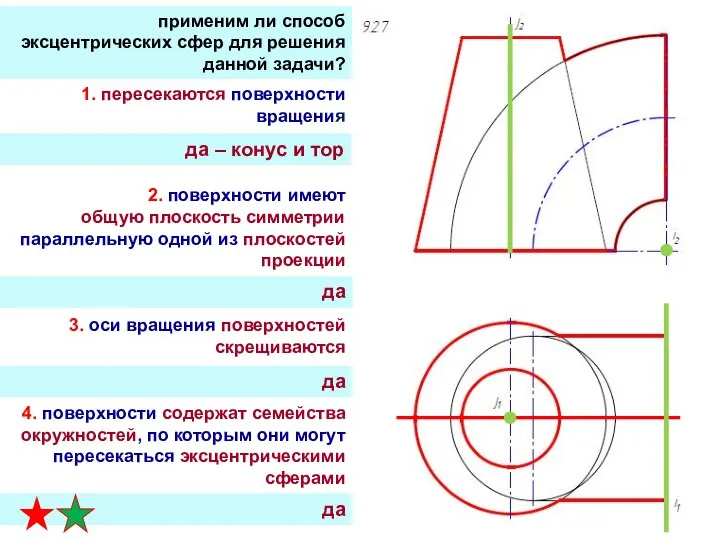
- 35. применим ли способ эксцентрических сфер для решения данной задачи? 1. пересекаются поверхности вращения 3. оси вращения
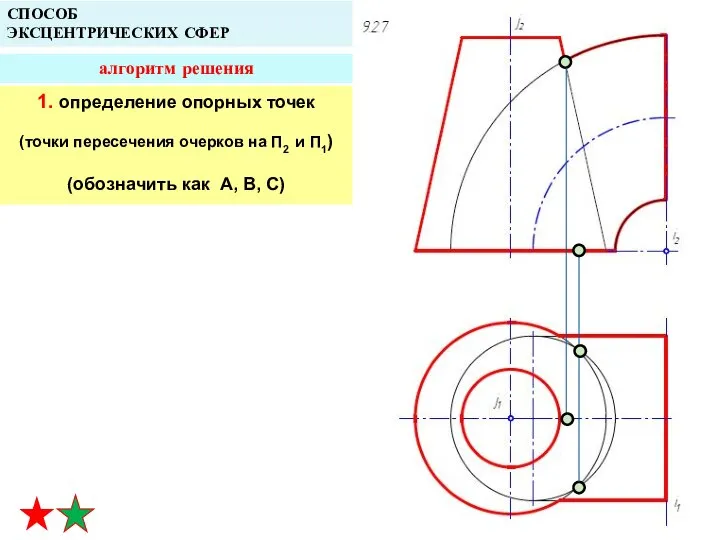
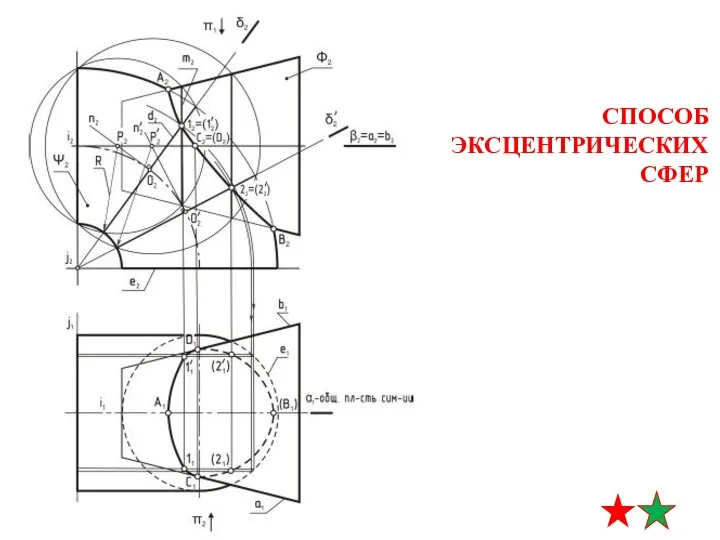
- 36. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 1. определение опорных точек (точки пересечения очерков на П2 и П1)
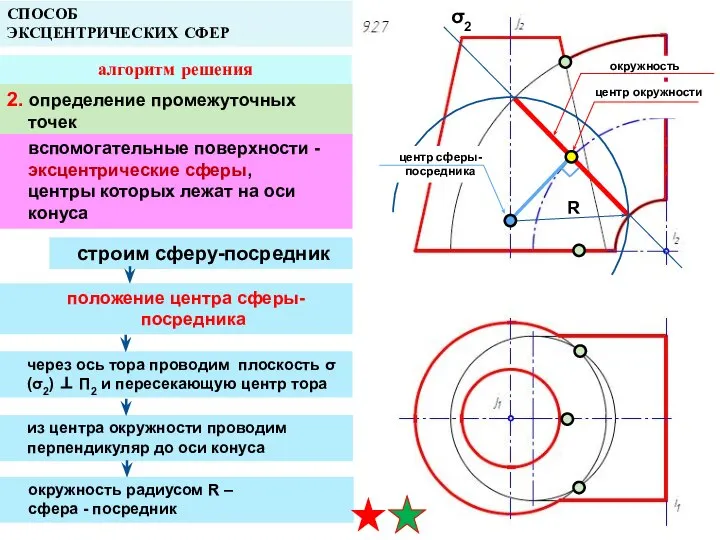
- 37. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 2. определение промежуточных точек вспомогательные поверхности - эксцентрические сферы, центры которых
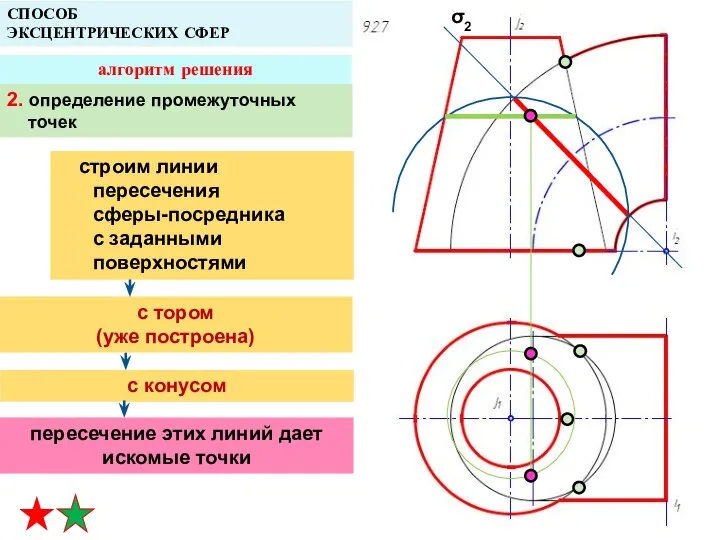
- 38. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 2. определение промежуточных точек строим линии пересечения сферы-посредника с заданными поверхностями
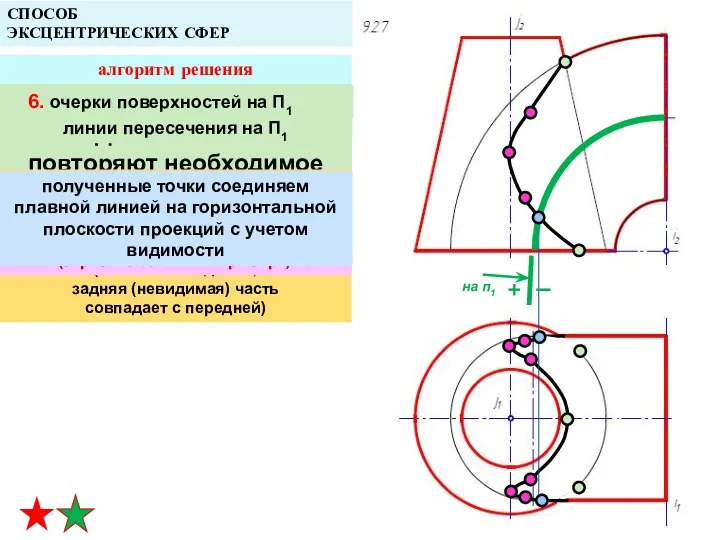
- 39. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Действия п. 2 повторяют необходимое количество раз для получения точек линии
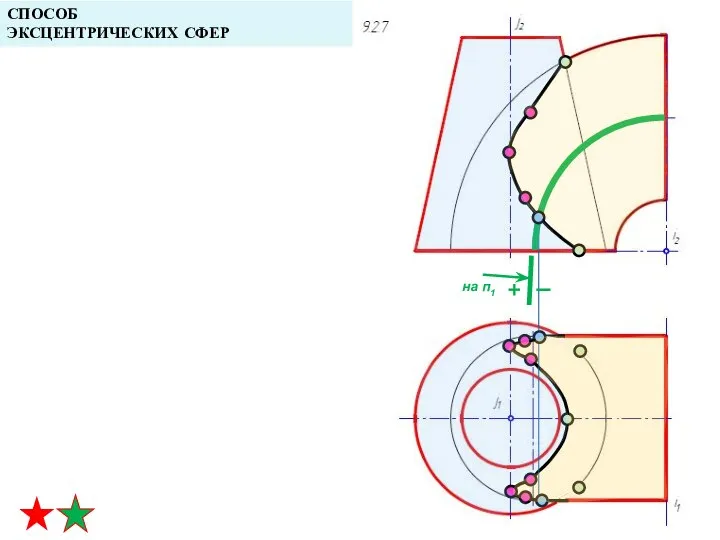
- 40. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР на п1
- 41. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
- 42. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР
- 43. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР
- 44. Частный случай пересечения поверхностей (Теорема Монжа)
- 46. Скачать презентацию



 МОУ «Андреевская СОШ»Судогодского районаВладимирской областиКоманда «НЕПОСЕДЫ»Учитель: Н.В.Пых
МОУ «Андреевская СОШ»Судогодского районаВладимирской областиКоманда «НЕПОСЕДЫ»Учитель: Н.В.Пых Повышение пенсионного возраста
Повышение пенсионного возраста Насекомоопыляемые растения
Насекомоопыляемые растения Биофизика
Биофизика Дети войны
Дети войны Анализ информатизации учебно-воспитательного процесса в ГБОУ лицей № 486Выборгского района Санкт-Петербурга
Анализ информатизации учебно-воспитательного процесса в ГБОУ лицей № 486Выборгского района Санкт-Петербурга Презентация на тему Человек и его деятельность 6 класс
Презентация на тему Человек и его деятельность 6 класс Расчет и построение чертежа конструкции женских брюк
Расчет и построение чертежа конструкции женских брюк Волшебная монотипия Бабочка
Волшебная монотипия Бабочка Православные праздники
Православные праздники Факультатив "Предпринимательский образ мышления" НИУ ВШЭ НН 28/09/2011
Факультатив "Предпринимательский образ мышления" НИУ ВШЭ НН 28/09/2011 Riddles
Riddles Почему он ушел? Примеры ошибок юзабилити и методы их определения.
Почему он ушел? Примеры ошибок юзабилити и методы их определения. Житие Сергия Радонежского Фрагмент кружкового занятия в 8 классе Учителя МОУ СОШ № 19 г. Кореновска Паньковой Елены Ивановны
Житие Сергия Радонежского Фрагмент кружкового занятия в 8 классе Учителя МОУ СОШ № 19 г. Кореновска Паньковой Елены Ивановны Winter - Зима
Winter - Зима American holidays and customs
American holidays and customs  Готовые решения на базе профессиональных CMSДмитрий Васильев
Готовые решения на базе профессиональных CMSДмитрий Васильев ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ НАЧАЛЬНОГО ОБЩЕГО ОБРАЗОВАНИЯвторого поколения
ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ НАЧАЛЬНОГО ОБЩЕГО ОБРАЗОВАНИЯвторого поколения Разграничение понятий акцентуация характера и психопатия
Разграничение понятий акцентуация характера и психопатия Индейцы
Индейцы Центр физического развития в средней группы №5
Центр физического развития в средней группы №5 Физические основы радиосвязи
Физические основы радиосвязи Романтизм в искусстве
Романтизм в искусстве 8 класс
8 класс Структура научного общества учащихся (НОУ). Детского технопарка
Структура научного общества учащихся (НОУ). Детского технопарка Tunahan Construction
Tunahan Construction Презентация на тему Водоемы нашего края
Презентация на тему Водоемы нашего края  СОКРОВИЩА ЧЕЛОВЕЧЕСТВАВсемирное наследие ЮНЕСКО
СОКРОВИЩА ЧЕЛОВЕЧЕСТВАВсемирное наследие ЮНЕСКО