Молекула в расчетных методах

Индексы i, j относятся к электронам; a, b – к ядрам;
M и m – массы ядер и электронов; ħ – постоянная Планка;
e – заряд электрона; Z- атомный номер;
Rab – расстояние между ядрами;
rae – расстояние между электроном и ядром;
ree – расстояние между электронами.

Разделить действия гамильтониана Ĥ на ядерную и электронную части точной Ψ(r,R) волновой функции нельзя. Это можно сделать только приближенно, если ввести электронную волновую функцию ΨЭ и сделать ее параметрически зависимой от расположения (R) ядер – это есть приближение Борна- Оппенгеймера.
Для этого фиксируется ядерная конфигурация (R) в предположении, что движение ядер происходит гораздо медленнее, чем движение электронов. В этом случае, молекулярная волновая функция Ψ(r,R) может быть записана как произведение электронной ΨЭ({r,R}) и ядерной ΨЯ({R}) компонент:
Ψ({r,R}) = ΨЭ({r,R}) ΨЯ({R}),
Обоснованность приближения Борна-Оппенгеймера: отношение масс электрона и ядра не больше, чем 1/1836, как это имеет место в случае самого легкого атома водорода.

ΨЭ({r,R}) – удовлетворяет уравнению:
Ĥэ ΨЭ({r,R}) = EэΨЭ({r,R}), где
ΨЯ({R}) – удовлетворяет уравнению:

Полная энергия молекул в приближении Борна Оппенгеймера есть:
Е = ЕЭ + ТЯ,
ТЯ – колебательно–вращательная энергия ядер. Величина ЕЭ называется адиабатическим потенциалом. Расчет ЕЭ для разных значений {R} дает поверхность потенциальной энергии (ППЭ), вдоль которой ядра перемещаются в пространстве.
Приближение Борна-Оппенгеймера несправедливо в том случае, когда энергия ядерных колебаний сопоставима с разностью энергий основного и возбужденных электронных состояний. При этом возникают так называемые вибронные состояния, а адиабатический потенциал теряет свой физический смысл. Следствием этого является важный структурный эффект Яна-Теллера.

Полная энергия системы Хартри-Фока для молекулы:
При учете приближения Борна-Оппенгеймера уравнения Хартри-Фока для молекулы можно решить численно, получив волновые функции Ψ(r,R) в виде таблиц. Однако извлечение химической информации из волновых функций, выраженных таким образом, представляет нелегкую задачу. Существует приближение, позволяющее существенно упростить как решение уравнений ХФ, так и интерпретацию результатов.
Смысл операторов и интегралов такой же как и для атома (Лекция 1). Только добавились взаимодействия ядер молекулы. Уравнение Хартри - Фока – аналогично уравнению Хартри-Фока атома.
Fψ (r,R) = E ψ (r,R)

Приближение МО ЛКАО. Уравнения Рутана.
Двигаясь по молекуле (состоящей из m атомов), каждый электрон
попадает под влияние поля ядра, вблизи которого он находится в
данный момент. Это означает, что описывающая этот электрон
волновая функция ϕi вблизи некоторого ядра (μ) должна быть близка к соответствующей АО. Поэтому каждую ϕi можно представить как линейную комбинацию всех АО (χμ) системы:
Коэффициенты разложения сiμ определяют “вес” каждой АО в каждой волновой функции – молекулярной орбитали (МО); одна и та же АО входит в разные МО с разными весами, т.е. эти коэффициенты различны для каждой МО.
ϕi(r) = ∑μm ciμχμ(r)

Другими словами - Теория метода Молекулярных Орбиталей исходит из предположения, что первоначально сближаются только ядра вместе с внутренними оболочками. При перекрывании пустых атомных орбиталей образуются пустые молекулярные орбитали, и лишь затем на них располагаются электроны.
Поскольку атомные орбитали локализованные на разных ядрах неортогональны, то для молекулы уравнения Хартри-Фока (Fψ(r,R) = εψ(r,R)), переписываются в виде:
Помножив это уравнение на χp* и проинтегрировав по объему dV (Лекция 1), получим в матричной форме записи:

Обобщенное уравнение на собственные значения называется уравнением Рутана:
F- матрица оператора Фока, S- матрица перекрытия для базисных
функций (АО), определяемые следующим образом:
Приближение МО ЛКАО ограничивает точность метода ХФ, поскольку реально в расчеты включается конечное число АО. Чтобы воспроизвести точное ХФ решение, потребовалось бы использовать в разложении бесконечное число функций – этот случай известен как хартри–фоковский предел.

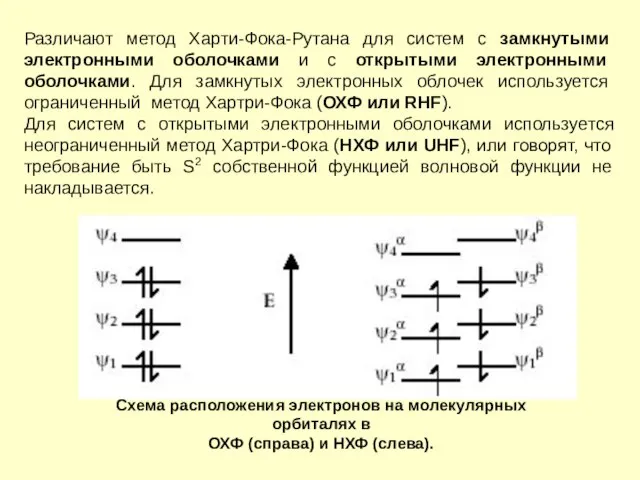
Различают метод Харти-Фока-Рутана для систем с замкнутыми электронными оболочками и с открытыми электронными оболочками. Для замкнутых электронных облочек используется ограниченный метод Хартри-Фока (ОХФ или RHF).
Для систем с открытыми электронными оболочками используется неограниченный метод Хартри-Фока (НХФ или UHF), или говорят, что требование быть S2 собственной функцией волновой функции не накладывается.
Схема расположения электронов на молекулярных орбиталях в
ОХФ (справа) и НХФ (слева).

Однако из-за снятия указанного фундаментального ограничения на электронную волновую функцию, ее смысл в НХФ часто подвергается обсуждению. Например, в больших химических системах нередко получают НХФ - решения с собственными значениями S2, сильно отличными от истинных. Решения, которые показывают увеличение значений S2, называется "НХФ - нестабильными".
Недостаток метода Хартри–Фока. Метод использует приближение независимых частиц, а электронное взаимодействие учитывается в нем как сумма взаимодействий каждого электрона со средней электронной плотностью остальных электронов.
В действительности, между всеми электронами существует мгновенное кулоновское отталкивание, т.е. их движение коррелировано. Изменение энергии, вызванное этими мгновенными кулоновскими взаимодействиями, называется энергией корреляции:
Eкорр = Eточн – EХФ < 0.

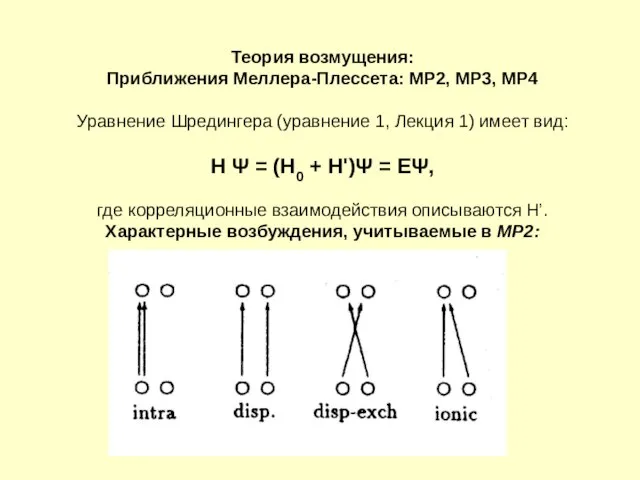
Теория возмущения:
Приближения Меллера-Плессета: MP2, MP3, MP4
Уравнение Шредингера (уравнение 1, Лекция 1) имеет вид:
Н Ψ = (Н0 + Н')Ψ = ЕΨ,
где корреляционные взаимодействия описываются H’.
Характерные возбуждения, учитываемые в MP2:

Конфигурационное взаимодействие
Волновая функция (Ψкв) ищется вариационным методом в виде линейной комбинации молекулярных орбиталей Ψк, которые описывают все возбужденные состояния молекулы.
Метод КВ применим к описанию возбужденных состояний , систем с открытыми оболочками и неравновесных систем, фотохимических реакций. Однако метод не удобен: реализация полноконфигурационного метода невозможна.

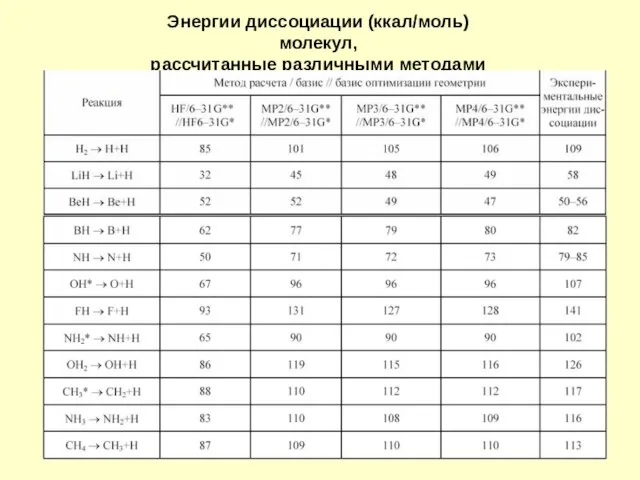
Энергии диссоциации (ккал/моль) молекул,
рассчитанные различными методами

Канонические и локализованные молекулярные орбитали
Молекулярные орбитали ϕi определяются как собственные функции
некоторого одноэлектронного гамильтониана F (оператор Хартри-Фока):
Fϕi = εiϕi
Симметрия фокиана F соответствует симметрии молекулы.
При этом собственные функции гамильтониана F тоже соответствуют
симметрии молекулы. МО обладающие такими свойствами симметрии
и определяемые как собственные функции одноэлектронного
гамильтониана называются каноническими молекулярными
орбиталями.

В качестве примера – молекула метана: CH4
( точечная симметрия Td)
Канонические МО:
ϕ1 = a(2sC) + ½ b (1sH1+1sH2+1sH3+1sH4) (E= εa1)
ϕ2 = c(2px C) + ½ d (1sH1+1sH2-1sH3-1sH4) (E= εt2)
ϕ3 = c(2py C) + ½ d (1sH1-1sH2 +1sH3-1sH4) (E= εt2)
ϕ4 = c(2pz C) + ½ d (1sH1-1sH2 - 1sH3 +1sH4) (E= εt2)
орбиталь ϕ1 является полносимметричной
(неприводимое представление a1 тетраэдрической
группы симметрии Td – c энергией εa1).
Орбитали ϕ2, ϕ3, ϕ4 - преобразуются по трехмерному
представлению t2 и соответствуют одному и тому же
трехмерному вырожденному одноэлектронному уровню εt2.

Указанные канонические МО можно преобразовать
в локализованные МО :
fi = c(hiC) + d(1sHi) + (a-c)(2sC) +1/2(b-d) (1sH1+1sH2+1sH3+1sH4)
где hiC (гибридные АО атома углерода):
h1C = ½ (2sC + 2pxC + 2pyС +2pzC);
h2C = ½ (2sC + 2pxC - 2pyС - 2pzC);
h3C = ½ (2sC - 2pxC + 2pyС - 2pzC);
h4C = ½ (2sC - 2pxC - 2pyС + 2pzC);
Локализацию можно считать абсолютной, если a=c, b=d.
Но в действительности эти равенства не выполняются строго.
Каждой локализованной МО соответствует одно общее
значение энергии:
ε = (εa1+3εt2)/4

Теория метода Молекулярных Орбиталей исходит из предположения, что первоначально сближаются только ядра вместе с внутренними оболочками. При перекрывании пустых атомных орбиталей образуются пустые молекулярные орбитали, и лишь затем на них располагаются электроны. МО имеет вид:
Метод Валентных Связей предполагает, что образование молекул происходит при сближении целых атомов. МО имеет вид:
Где ΨiBC – произведение атомных функций

Примеры: метод ВС метод ЛКАО МО
e1 e2
атомы H A B
Ψ1 = ΨA(e1) * ΨB(e2)
Ψ2 = ΨA(e2) * ΨB(e1)
Ψ3 = ΨA(e1) * ΨA(e2)
Ψ4 = ΨB(e1) * ΨB(e2)
1 = С1ΨA(e1) + С2ΨB(e2)
Ψ= C1 Ψ1+ C2 Ψ2 + C3 Ψ3 + C4 Ψ4

Метод ВС предполагает, что атомы в молекулах сохраняют во многом свою индивидуальность, а эффект химической
связи рассматривается как возмущение, приводящее к обмену электронами и их спариванию в соответствии с требованием принципа Паули. Многоэлектронная волновая функция Ψ строится как линейная комбинация линейно независимых антисимметризованных произведений наборов АО со спиновыми частями. Каждая функция ΨiBC соответствует набору атомов в определенных электронных конфигурациях и называется валентной структурой (ВС). Параметры орбиталей в ВС и их веса определяются с помощью вариационного принципа. Электронное строение и свойства системы, представляются в методе ВС как среднее по различным ВС, число, которых может быть очень велико. На первых стадиях развития квантовой химии эта взвешенная суперпозиция валентных структур получила название резонансный гибрид, а сами ВС называются резонансными. Метод ВС дает более наглядное представление о химических связях.

Какой метод лучше?
Метод ВС дает более наглядное представление о химических связях
Метод МО не требует представлений о резонансных структурах – их заменило представление о многоцентровых связях.
Достоинства метода МО: метод «смог» объяснить ряд эффектов, необъяснимых с точки зрения метода ВС.
Это эффект парамагнетизма молекулы кислорода – с позиции метода ВС – все электроны (16) использованы на образование связи и молекула должна быть диамагнитная.
С точки зрения метода МО – т.е. если рассмотреть заполнение МО электронами, то на самой высокой по энергии и дважды вырожденной разрыхляющей π*2p орбитали находится 2 электрона. По принципу Паули – эти два электрона должны находиться на разных орбиталях. Отсюда парамагнетизм.