Содержание
- 2. Основы теории информации В окружающей действительности часто встречаются ситуации, когда может произойти число событий, большее чем
- 3. Основы теории информации Если все из возможных событий N равновероятны, то количество информации I выражается формулой:
- 4. Основы теории информации Задолго до появления компьютеров вообще, и тем более использующих двоичную систему счисления, в
- 5. Основы теории информации Разновероятные события. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций,
- 6. Основы теории информации В 1948 г. американский инженер и математик К. Шеннон предложил формулу для вычисления
- 7. Основы теории информации Задачи. 1. Определить количество информации, получаемое при реализации одного из событий, если бросают:
- 8. Основы теории информации Самостоятельно решить задачи: 1. Вероятность первого события составляет 0,5, а второго и третьего
- 9. Основы теории информации Рассмотренный выше способ определения количества информации, получаемого в событиях, которые уменьшают неопределенность наших
- 10. Основы теории информации При таком подходе, термин «событие» ассоциируют с понятием «сообщение». Сообщение состоит из некоторого
- 11. Основы теории информации Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации,
- 12. Основы теории информации Единица и ноль Хотя внутренний язык некоторых компьютеров первого поколения был основан на
- 13. Основы теории информации Почему именно основание два ? Система счисления с основанием два более всего соответствует
- 14. Основы теории информации Биты, байты и полубайты Решив представлять данные последовательностями единиц и нулей, минимальную единицу
- 15. Основы теории информации Двоичные числа Компьютер использует наборы нулей и единиц для представления всего, с чем
- 16. Основы теории информации От десятичных к двоичным В двоичной системе счисления, как и в десятичной, значение
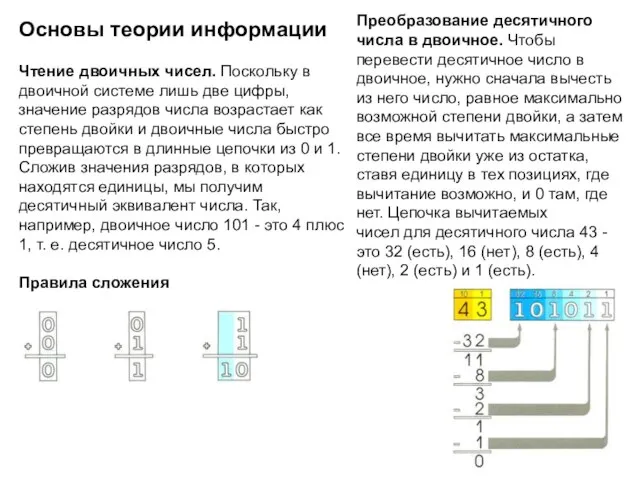
- 17. Основы теории информации Чтение двоичных чисел. Поскольку в двоичной системе лишь две цифры, значение разрядов числа
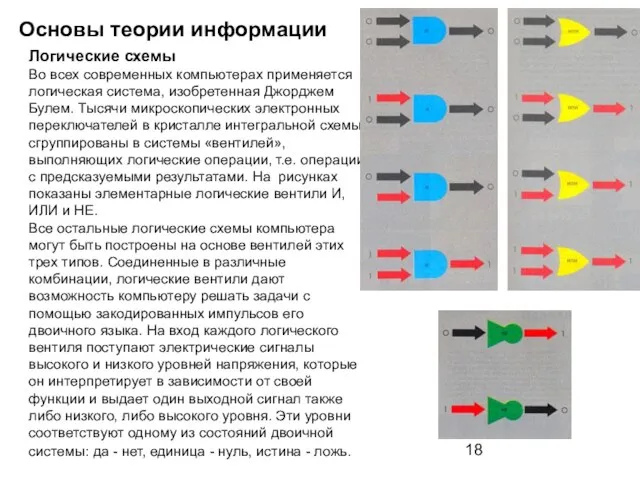
- 18. Основы теории информации Логические схемы Во всех современных компьютерах применяется логическая система, изобретенная Джорджем Булем. Тысячи
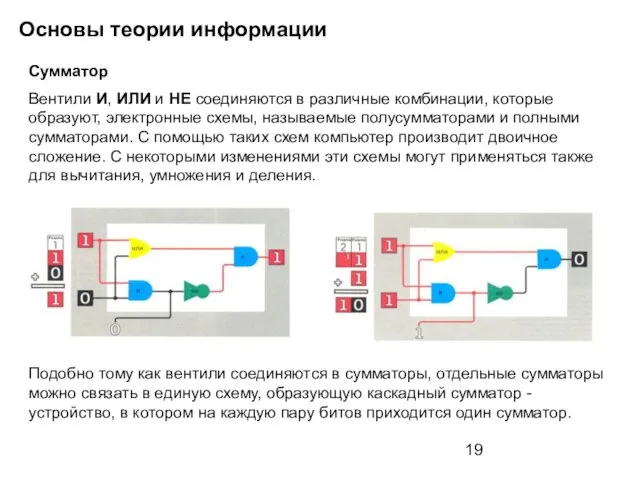
- 19. Основы теории информации Сумматор Вентили И, ИЛИ и НЕ соединяются в различные комбинации, которые образуют, электронные
- 20. Основы теории информации В примере два четырехбитных числа (справа) складываются при помощи каскада из 4 сумматоров.
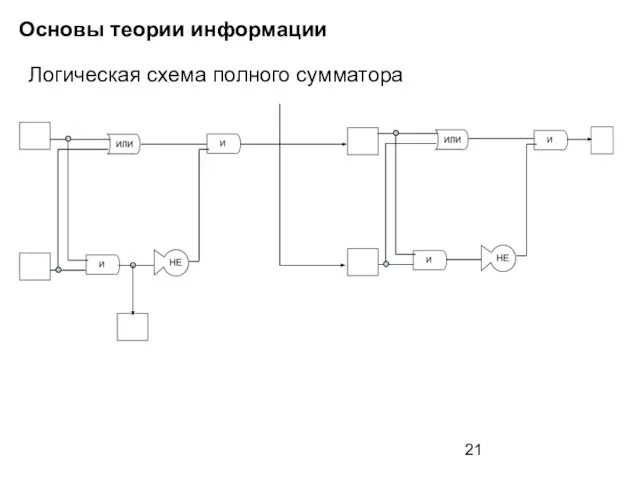
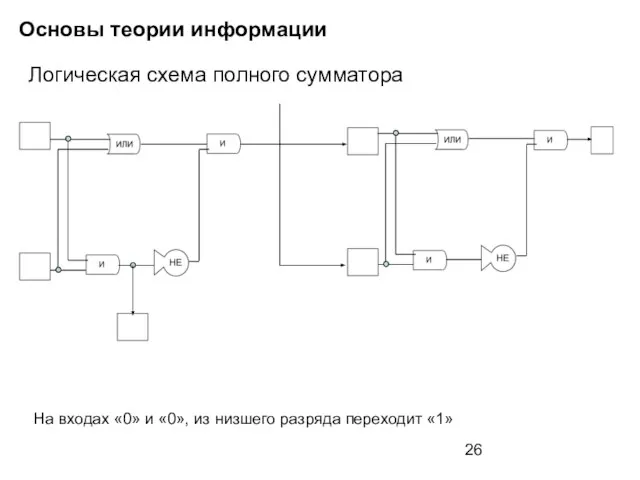
- 21. Основы теории информации Логическая схема полного сумматора
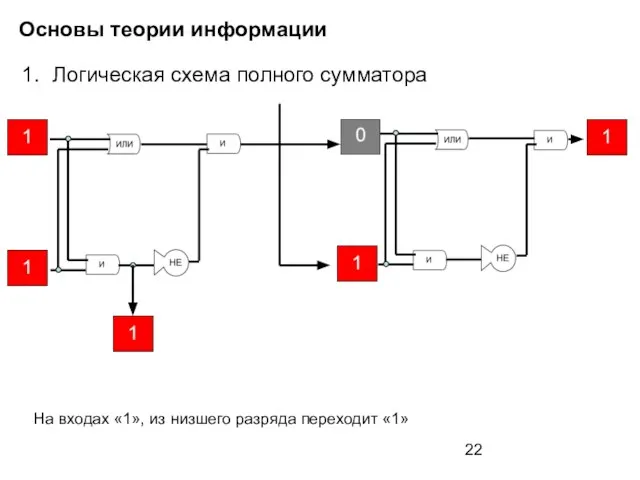
- 22. Основы теории информации Логическая схема полного сумматора На входах «1», из низшего разряда переходит «1»
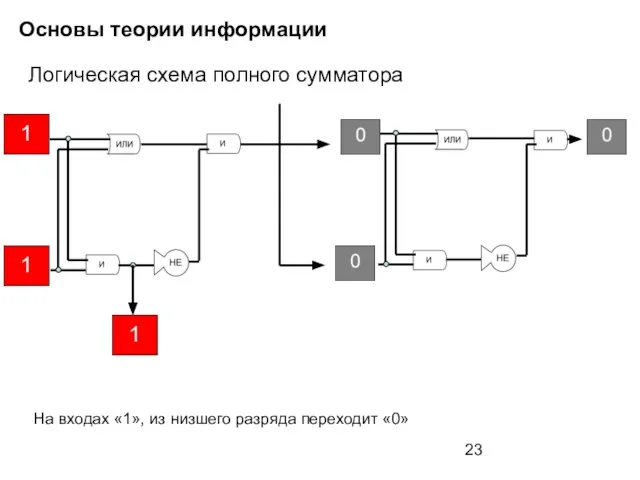
- 23. Основы теории информации Логическая схема полного сумматора На входах «1», из низшего разряда переходит «0»
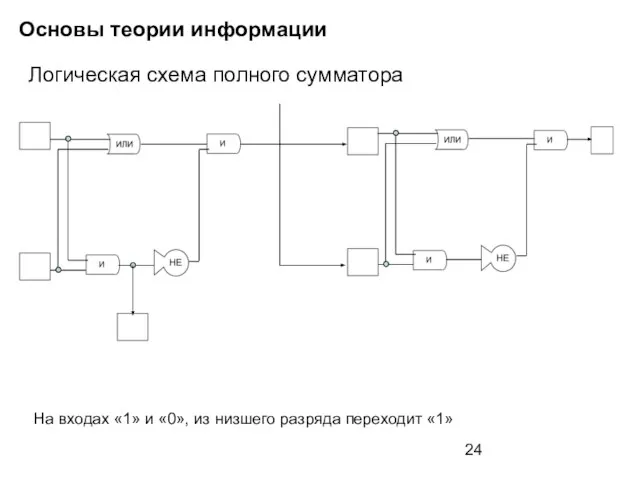
- 24. Основы теории информации Логическая схема полного сумматора На входах «1» и «0», из низшего разряда переходит
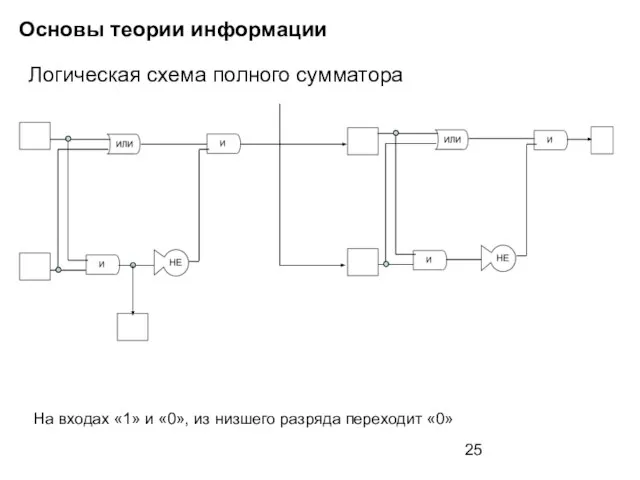
- 25. Основы теории информации Логическая схема полного сумматора На входах «1» и «0», из низшего разряда переходит
- 26. Основы теории информации Логическая схема полного сумматора На входах «0» и «0», из низшего разряда переходит
- 28. Скачать презентацию
















 Бессмертная комедия А. С. Грибоедова «Горе от ума»
Бессмертная комедия А. С. Грибоедова «Горе от ума» Урок коллективного посещения в 5 классе
Урок коллективного посещения в 5 классе ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы.
ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы. Ранения. Первая медицинская помощь
Ранения. Первая медицинская помощь Совершенствование сервисно-транспортной инфраструктуры придомовых территорий
Совершенствование сервисно-транспортной инфраструктуры придомовых территорий СТЕКЛЯННЫЕ ТОВАРЫ
СТЕКЛЯННЫЕ ТОВАРЫ Применение электролиза. Основная химическая промышленность
Применение электролиза. Основная химическая промышленность Маршрут прогулки по городу Борисоглебск
Маршрут прогулки по городу Борисоглебск Региональный студенческий хакатон ООО АИС город
Региональный студенческий хакатон ООО АИС город Берегите зрение
Берегите зрение Конкурентные преимущества и перспективы развития казахстанского фондового рынка
Конкурентные преимущества и перспективы развития казахстанского фондового рынка Древние восточные церкви. Православие за рубежом в xх – xxi вв
Древние восточные церкви. Православие за рубежом в xх – xxi вв Pro-психологов: психологическая служба образовательной организации
Pro-психологов: психологическая служба образовательной организации ST Main Page
ST Main Page Лекарственная аллергия
Лекарственная аллергия Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация Развитие координационных способностей у юных борцов вольного стиля
Развитие координационных способностей у юных борцов вольного стиля Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони
Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ
МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ Политический конфликт
Политический конфликт Чемпионат и первенство города Ярославля по зимнему триатлону
Чемпионат и первенство города Ярославля по зимнему триатлону AI автомобиля в изменчивом мире на примере Ex Machina
AI автомобиля в изменчивом мире на примере Ex Machina Восприятие речи
Восприятие речи Конаково
Конаково Сударыня - Масленица
Сударыня - Масленица Візуальний контакт під час ділової комунікації
Візуальний контакт під час ділової комунікації Технологии проведения избирательной кампании
Технологии проведения избирательной кампании Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»
Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»