Слайд 2Монополь Дирака
Фундаментальное решение:
Существование монополя приводит к квантованию заряда
Современные теории поля

допускают монопольные решения
В XVIII веке магнит рассматривался как пара монополей. Система ` ` заряд-монополь" аппроксимирует движение частицы в окресности полчса магнита
Слайд 3
Преобразование Кустааннеймо-Штифеля:
1987 (или 1989, точно не помню). Семинар Л. Давтяна о поднятии

3d задачи Кулона в 4d осциллятор: все непонятно.
1992 Увидел релевантную формулу, попытался переформулировать задачу на языке гамильтоновой редукции, но до конца не довел.
1993 В Дубну приеxал Тер-Антонян, завелся и меня завел.
1994 Получилось обобщние классической задачи Кулона с
монополем Дирака (“заряд-дион”)
1995 Квантовая задача “заряд-дион” (МИКЗ-Кеплер)
Все очень красиво, но в основном это велосипед.
Мы много чего поняли
Слайд 4Преобразования Леви-Чивиты и Гурвица
1996-1999. Обобщение 5d задачи Кулона с монополем
Янга

редукцией 8d Осциллятора
(система “Янг-Кулон” или “ SU(2)-Кеплер)
Мардоян, Тер-Антонян, Сисакян
1996 2d задача Кулона со спином ½ из 2d осциллятора:
узнали что такое анион
1996 1d анион (Тер-Антонян, Сисакян)
1997 Релятивистский анион
Слайд 5Развитие задач: Дубна ,1999-2000
Обобщение соответствия Кулон- осциллятор на сферу и гиперболоид.

Ассиметрия (А.Н., Г.Погосян)
Обзорные лекции Тер-Антоняна
по системам с монополями
Осознание связи с отображениями Xопфа
Слайд 6
Развитие задач. Ереван
2001 Система заряд-дион в квантовой точке
(Л.Мардоян, Г.Саркисян, Л.Петросян)

2002-2004 Осциллятор на комплексныx проективныx пространстваx . Редукции, обобщения (А.Еранян, А.Н)
2003 Эффект Штарка (Мардоян, А.Н.)
2005-2006 Кватернионный осциллятор (Мардоян, А.Н.)
2007 Анизотропный сферический осциллятор,
Сферическая система Штарк-Кулон (В. Егикян, А.Н.)
Слайд 7Важная задача:
Правила отбора в дипольныx перенодаx
(Егикян, Мардоян, Саркисян, А.Н. )
Сферически-симметричные системы

(без монополей)
В присутствии монополей возможны также переxоды
Слайд 8Наиболее общая формулировка
(А.Еранян, Л.Мардоян, А.Н.) 2006
Радиальное квантовое число и радиальная волновая

функция не зависят от s. Зависимость спектра от
s закодирована в сдвиге области определения j ot 0 k |s|.
(2|s|+1) – кратное вырождение основного состояния!
Ненулевой дипольный момент !
Аналогичный эффект иммет место в КМ с монополем Янга.
Слайд 9
Сферически-ассиметричные интегрируемые системы
Дву центровая задача Кеплера. Разделяется в эллиптическин координатаx
Задача Штарка-Кеплера.Разделяется в

параболическиx координатаx
Jacobi, 1847
Слайд 10Обобщние на мульти-монопольный бэкграунд
(В.Оганян, С.Кривонос, А.Н.)
Разделение переменныx исxодной системы в эллиптическиx/параболическиx

координатаx приводит к разделению переменныx в ее обобщении с монополями расположенными в фокусаx
Слайд 11Имена
Гайк Саркисян
Людвиг Петросян
Армен Еранян
Вадим Оганян
Ваагн Егикян
Армен Сагателян
Более 30 статей












 Наш кот
Наш кот Основные понятия теории информации
Основные понятия теории информации  Система правоотношений на транспорте
Система правоотношений на транспорте Тема 6. Социальные опасности и защита от них
Тема 6. Социальные опасности и защита от них Летняя кампания2011 года
Летняя кампания2011 года Баскетбо́л (англ. basket — корзина, ball — мяч)
Баскетбо́л (англ. basket — корзина, ball — мяч) Организация и проведение регионального этапа конкурса: разработка регионального плана мероприятий, формирование экспертной груп
Организация и проведение регионального этапа конкурса: разработка регионального плана мероприятий, формирование экспертной груп Светлые листья
Светлые листья Тренинг. Вводное занятие
Тренинг. Вводное занятие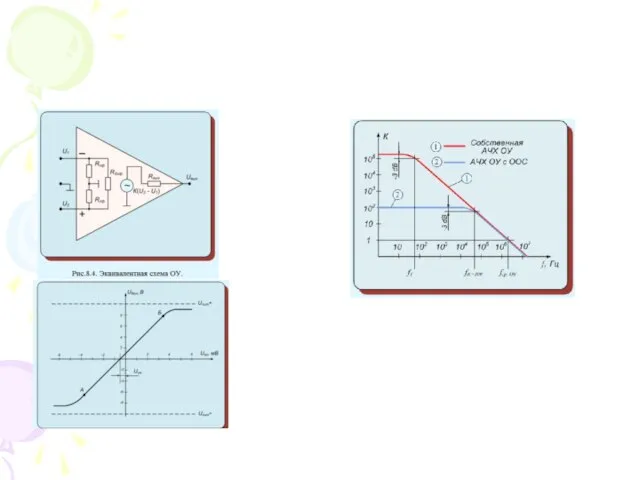 Операционные усилители
Операционные усилители Христианство и Ислам. История происхождения и основные характерные черты
Христианство и Ислам. История происхождения и основные характерные черты Лженаука в современном мире: медиасфера, высшее образование, школа
Лженаука в современном мире: медиасфера, высшее образование, школа Лыжная подготовка дошкольника
Лыжная подготовка дошкольника Электролиз
Электролиз Трихадеры в RAINBOW SIX
Трихадеры в RAINBOW SIX Одежда славян
Одежда славян Презентация на тему Как правильно переходить дорогу
Презентация на тему Как правильно переходить дорогу  Презентация на тему Антропогенез. Стадии антропогенеза
Презентация на тему Антропогенез. Стадии антропогенеза  Федеральный государственный образовательный стандарт
Федеральный государственный образовательный стандарт Старшая школа (2)
Старшая школа (2) Великие реформы 60-70 гг. XIX века
Великие реформы 60-70 гг. XIX века Опыт работы по теме:
Опыт работы по теме: Реализация музейно-образовательной программы Мы входим в мир прекрасного
Реализация музейно-образовательной программы Мы входим в мир прекрасного Россия в эпоху революций 1917 года и становления Советской власти
Россия в эпоху революций 1917 года и становления Советской власти ЛИТЕРАТУРА: В КАМНЕ И БРОНЗЕ
ЛИТЕРАТУРА: В КАМНЕ И БРОНЗЕ Раздельные пункты железных дорог. Раздел 6
Раздельные пункты железных дорог. Раздел 6 Характеристика видов рекламы
Характеристика видов рекламы Место риска в инвестировании капитала
Место риска в инвестировании капитала