Морской пейзаж

Проблема:
построение графиков функций с помощью преобразований.
Цель:
познакомиться с преобразованиями графиков элементарных функций с дальнейшим применением их на практике.
Задачи:
закрепить знания о видах функций;
познакомиться с правилами преобразования графиков;
научиться строить графики функций с модулем с помощью преобразований;
познакомиться с понятием кусочной функции;
использовать компьютерные технологии для защиты проекта.

План работы над проектом:
изучение теории вопроса;
выполнение практической части по этапам (построение графиков);
работа над презентацией проекта.
работа в Paint по оформлению работы.
Используемые источники:
материалы элективного курса «Графики улыбаются»;
учебник «Алгебра», 9 класс;
журнал «Математика в школе»;

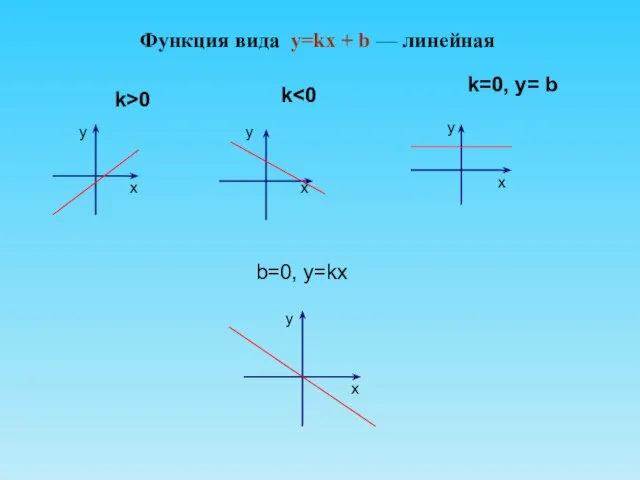
Функция вида y=kx + b — линейная
b=0, y=kx
у
х
х
х
х
у
у
у
k>0
k=0, y= b
k<0

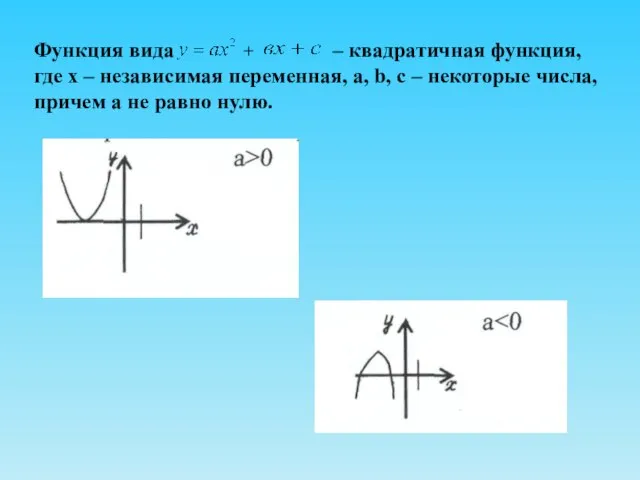
Функция вида + – квадратичная функция,
где х – независимая переменная, a, b, c – некоторые числа, причем a не равно нулю.

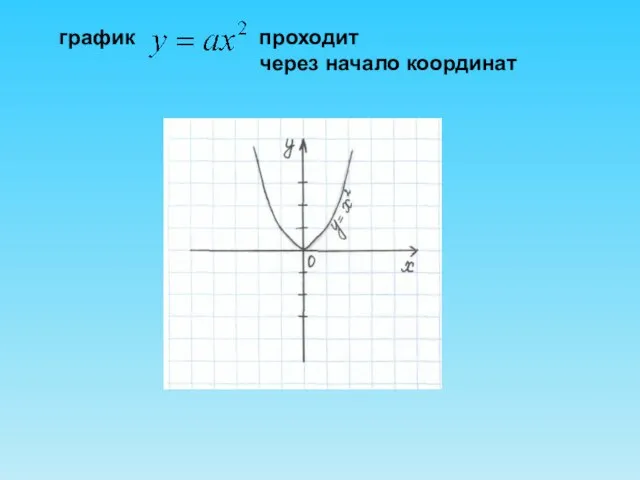
график проходит
через начало координат

Функция вида у = | х |
По определению модуля, функцию у = | х |
можно задать, следующим образом:
у = | х |= х, при х≥0
- х, при х≤0

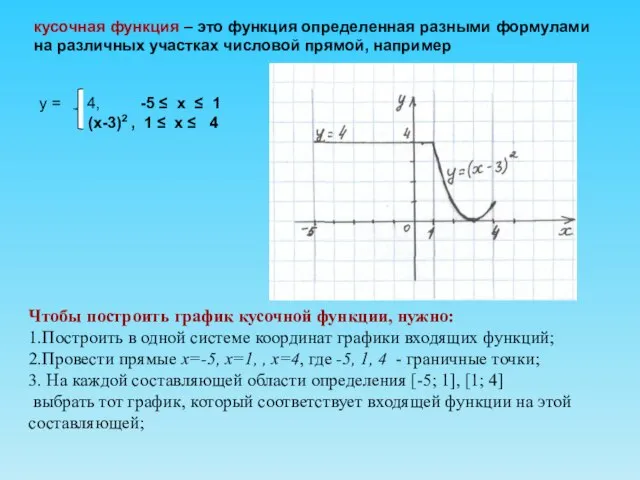
кусочная функция – это функция определенная разными формулами на различных участках числовой прямой, например
у = 4, -5 ≤ х ≤ 1
(х-3)2 , 1 ≤ х ≤ 4
Чтобы построить график кусочной функции, нужно:
1.Построить в одной системе координат графики входящих функций;
2.Провести прямые x=-5, x=1, , x=4, где -5, 1, 4 - граничные точки;
3. На каждой составляющей области определения [-5; 1], [1; 4]
выбрать тот график, который соответствует входящей функции на этой составляющей;

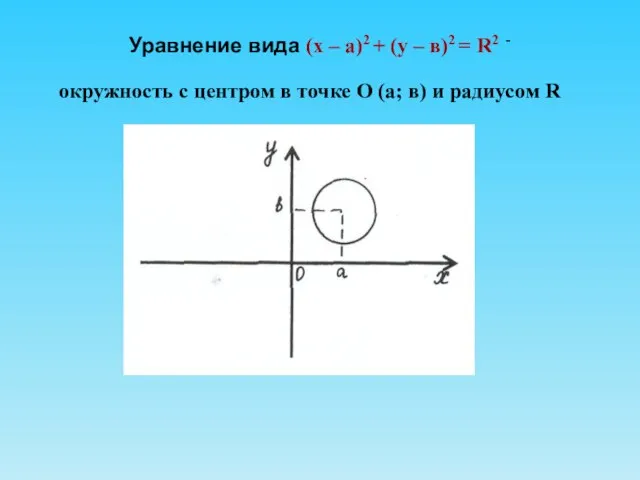
Уравнение вида (х – а)2 + (у – в)2 = R2 -
окружность с центром в точке О (а; в) и радиусом R

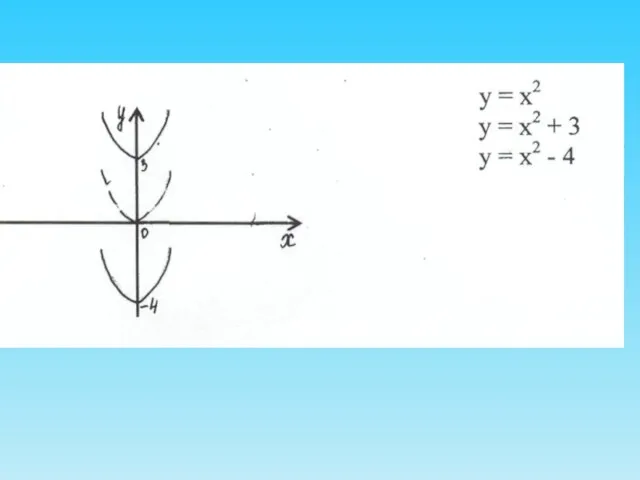
Преобразования графиков
1. у=f(х) + А – параллельный перенос вдоль оси ОУ. Если А > 0, то параллельный перенос графика вдоль оси ОУ вверх.
Если А < 0, то параллельный перенос графика вдоль оси ОУ вниз.

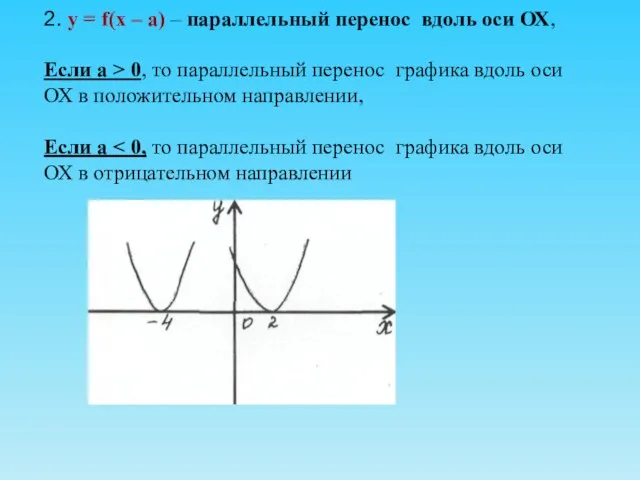
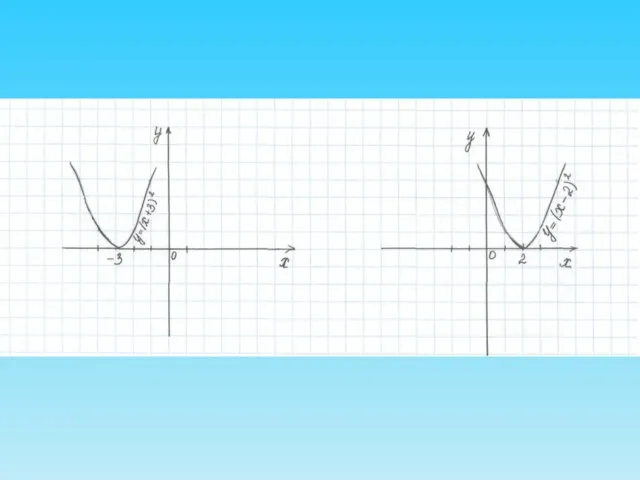
2. у = f(х – а) – параллельный перенос вдоль оси ОХ,
Если а > 0, то параллельный перенос графика вдоль оси ОХ в положительном направлении,
Если а < 0, то параллельный перенос графика вдоль оси ОХ в отрицательном направлении

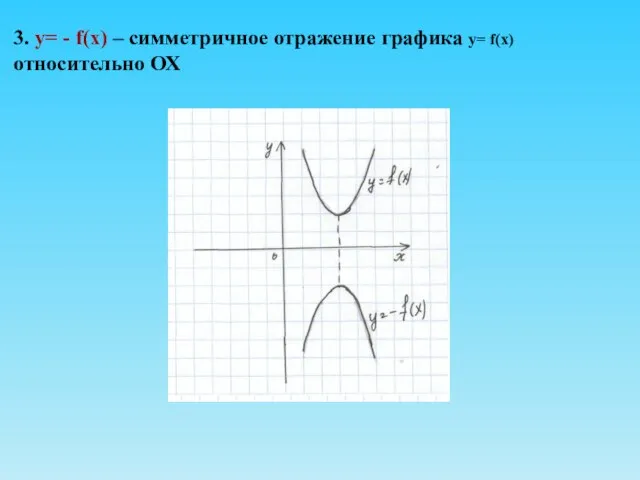
3. у= - f(х) – симметричное отражение графика у= f(х)
относительно ОХ

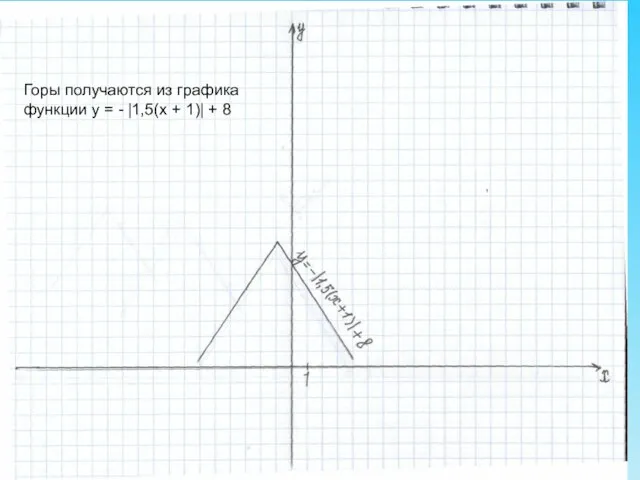
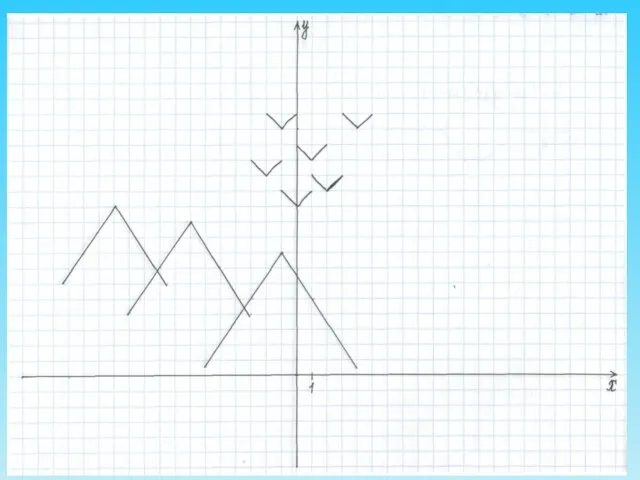
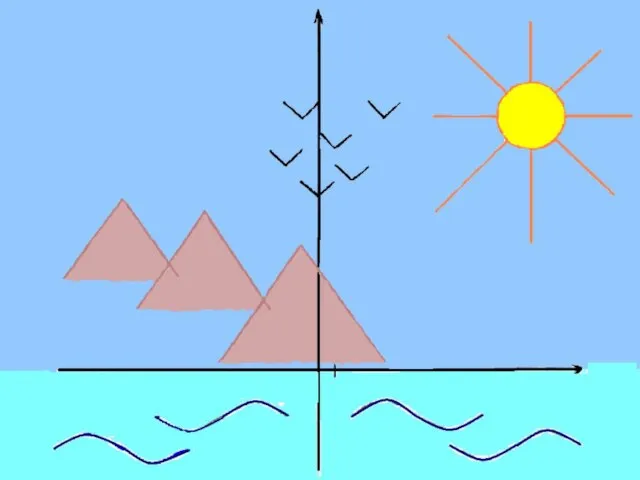
Практическая часть
1. Построение гор
Горы получаются из графика функции у = - |1,5(х + 1)| + 8 ,
Для этого сначала построили график у = - |1,5х| и выполнила преобразования по следующей схеме.
1. Параллельный перенос вдоль оси ОХ на 1 единицу влево и
параллельный перенос вдоль оси ОУ на 8 единиц вверх, получим у = - |1,5(х + 1)| + 8 на промежутке [-6; 4]

Горы получаются из графика функции у = - |1,5(х + 1)| + 8

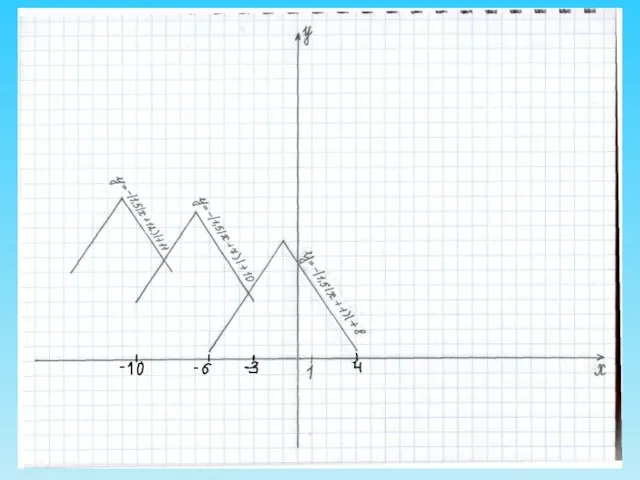
Аналогично
у = -| 1,5(х + 7) | + 10 на промежутке [-10; -3]
у = -| 1,5( х +12 ) | + 11 на промежутке [-16; -9]

Построение чаек
Чайки получаются из графика функции у =| х |.
Преобразования выполним по следующей схеме.
1. Параллельный перенос вдоль оси ОУ на 11 единиц вверх получим
у =| х |+ 11 на интервале [-1; 1]
2. Параллельный перенос вдоль оси ОХ на 2 единицы вправо и
параллельный перенос вдоль оси ОУ на 12 единиц вверх, получим у =| х – 2 | + 12 на интервале [1; 3]
Аналогично
у =| х – 1 | +14 - на интервале [0; 2]
у =| х – 4 |+ 16 - на интервале [3; 5]
у =| х + 2 |+ 13 - на интервале [-3; -1]
у =| х + 1 |+ 16 - на интервале [-2; 0].
Таким образом, изобразила шесть чаек.

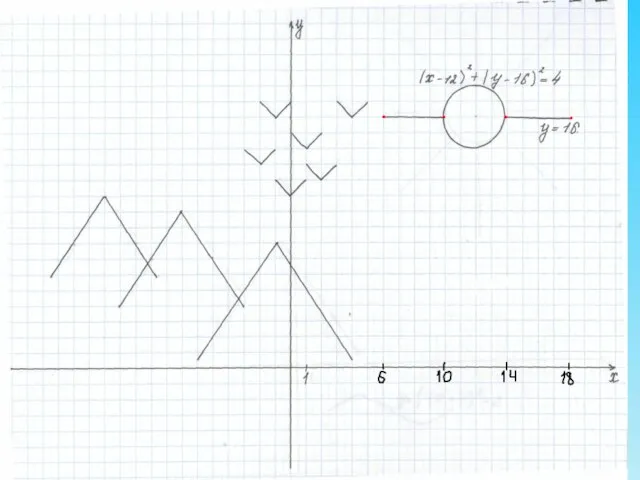
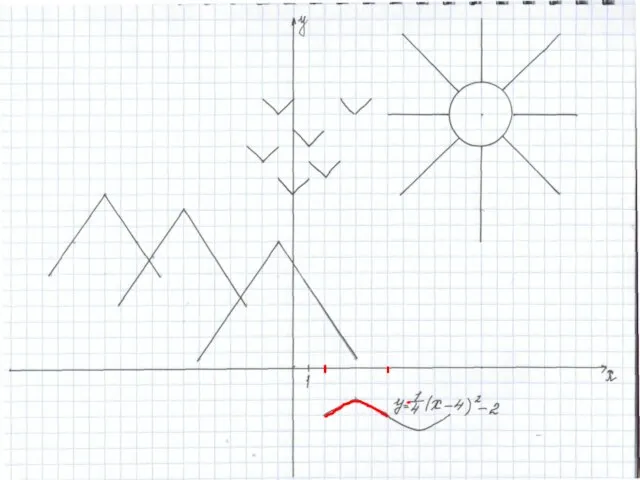
Построение солнца.
Уравнение окружности:
(х – 12)2 + (х – 16)2 = 4.
Центр окружности точка О(12;16) и радиус R=2.
Лучи
1ый луч: у = 16 прямая параллельная оси ОХ. Построим на промежутке
[6; 10] U[14; 18]
2ой луч: Прямая у = х + 4.
Для того чтобы найти интервалы ограничения найдем точки пересечения с окружностью.
(х – 12)2 + (у – 16)2 = 4
у = х + 4

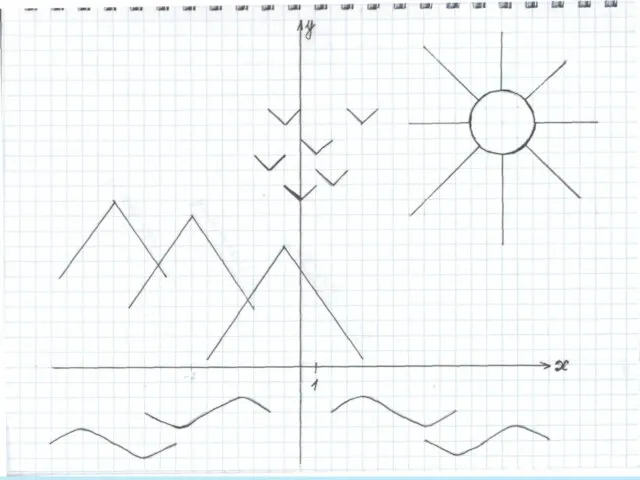
4. Построение волн