МОУ «Красноярская основная общеобразовательная школа» Зырянского района. Учитель математики: Кудинова Ирина Николаевна.
Содержание
- 2. МАСТЕР - КЛАСС ОРИГАМИ И МАТЕМАТИКА
- 3. Японская мудрость издревле гласит: "Великий квадрат не имеет пределов. Попробуй простую фигурку сложить, И вмиг обретёшь
- 4. Оригами ? искусство складывания из бумаги, древнее японское изобретение и одно из самых распространённых в настоящее
- 5. Почему так трудно идет изучение геометрии в школе? Трудности усвоения – следствие традиционного обучения в начальных
- 6. В оригами заложены богатые возможности для развития геометрических представлений учащихся, ознакомления их с максимально богатым набором
- 7. . Построение простейших моделей классического или модульного оригами начинается с построения либо диагонали, либо средней линии
- 8. ОРИГАМИ - математическая теория, так как в ней работает аксиоматический метод. Основные понятия оригаметрии: точка; линия
- 9. Итак, оригами даёт возможность: практически построить наглядную модель евклидовой геометрии и научиться работать на ней; развить
- 10. Рассмотрим возможные формы работы с фигурой оригами на примере «Восьмиугольной звезды». I этап работы – построение
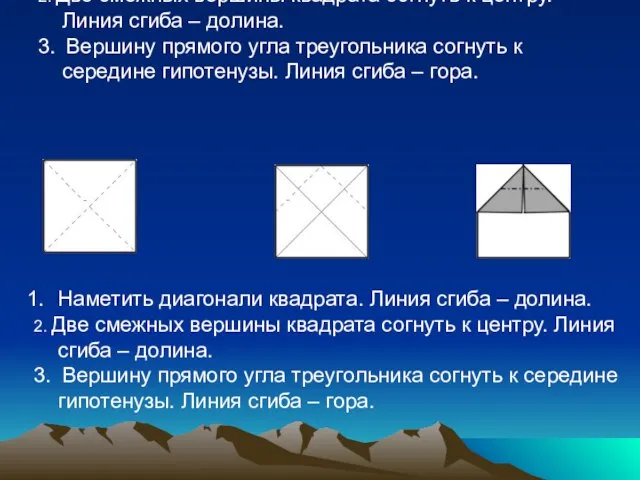
- 11. Наметить диагонали квадрата. Линия сгиба – долина. 2. Две смежных вершины квадрата согнуть к центру. Линия
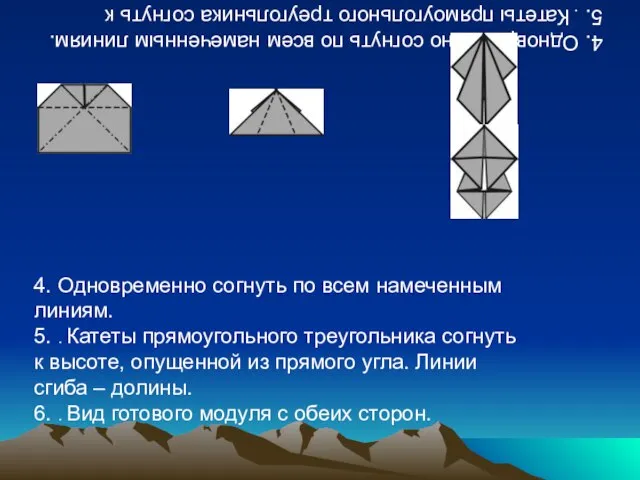
- 12. 4. Одновременно согнуть по всем намеченным линиям. 5. . Катеты прямоугольного треугольника согнуть к высоте, опущенной
- 13. 7. На рисунке показан один из возможных способов соединения двух модулей. 8. . И представлена фигура,
- 14. Построенная звезда может быть художественной моделью правильного восьмиугольника. И поэтому ее можно включать в плоские композиции,
- 15. Алгоритм изготовления кубика. 1. Согнуть лист пополам
- 16. 2.Разверните лист. Загните правый край листа к центральной линии сгиба.
- 17. 3. Повторить то же самое с левой стороной.
- 18. 4.Совместить левый верхний угол с верхним краем листа.
- 19. 5.Правый нижний угол совместить с нижним краем листа
- 20. 6.Левый уголок спрятать внутрь первоначального сгиба листа
- 21. 7. Проделать то же самое с правым уголком
- 22. 8.Маленький правый треугольник спрятать внутрь
- 23. 9. Проделать то же самое с левым треугольником
- 24. 10.Перевернуть заготовку и совместить верхний и нижний треугольники до получения квадрата.
- 25. 11.Мы получили следующую заготовку
- 26. 12.Таких заготовок мы изготавливаем 6 штук и вставляем поочерёдно уголки в кармашки.
- 27. 13. В результате мы получили вот такой кубик
- 32. Скачать презентацию



























 Моделирование фартуков
Моделирование фартуков Apple iPhone X Space Gray от 79990руб
Apple iPhone X Space Gray от 79990руб Психолого-педагогические условия формирования самосознания у детей дошкольного возраста с задержкой психического развития
Психолого-педагогические условия формирования самосознания у детей дошкольного возраста с задержкой психического развития Лезгины
Лезгины Понятие о профессии. Лекция 2
Понятие о профессии. Лекция 2 Курс Финансы
Курс Финансы Аналоговые и цифровые электронные цепи
Аналоговые и цифровые электронные цепи Презентация на тему Население и страны Евразии
Презентация на тему Население и страны Евразии  Учет лесоматериалов
Учет лесоматериалов Виртуальное путешествие в музей – заповедник «Михайловское»
Виртуальное путешествие в музей – заповедник «Михайловское» Вас приветствует кружковое объединение "Юный физик"
Вас приветствует кружковое объединение "Юный физик" The story of miss moppet
The story of miss moppet Оптимизация и разработка системы гарнитуры дополненной реальности
Оптимизация и разработка системы гарнитуры дополненной реальности Изучение таблицы умножения
Изучение таблицы умножения Вакцинация
Вакцинация Los principios del estructuralismo europeo
Los principios del estructuralismo europeo Динамика чтения показывает, что в современном обществе среди молодежи значительно понизился интерес к чтению, как важному источн
Динамика чтения показывает, что в современном обществе среди молодежи значительно понизился интерес к чтению, как важному источн Муниципальное образовательное учреждение средняя общеобразовательная школа № 23
Муниципальное образовательное учреждение средняя общеобразовательная школа № 23 Система российского права. Законотворческий процесс
Система российского права. Законотворческий процесс Общаться с ребенком. Как?
Общаться с ребенком. Как? Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер
Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер Принудительный ввод плетей в оптимальную температуру
Принудительный ввод плетей в оптимальную температуру Уран
Уран Всероссийская политическая партия Мы - Будущее
Всероссийская политическая партия Мы - Будущее Миссия среди молодежи в условиях пандемии: духовные уроки и их осмысление
Миссия среди молодежи в условиях пандемии: духовные уроки и их осмысление Картинки из жизни классного руководителя
Картинки из жизни классного руководителя QoS в VoIP
QoS в VoIP Презентация на тему Водные млекопитающие
Презентация на тему Водные млекопитающие