MU_PZ_1

Теория дискретных устройств
Цель работы: Научиться по цифровой записи функции строить таблицу истинности, временную диаграмму, совершенные дизъюнктивную и конъюнктивную нормальные формы, применять свойства, тождества и законы алгебры логики, карты Карно для минимизации логических функций трех переменных.

Теория дискретных устройств
Порядок выполнения задания
1. Получить индивидуальное задание на практическое занятие (Приложение 1, Приложение 2).
2. По индивидуальному заданию составить таблицу истинности, доопределить безразличия (при их наличии) и построить временную диаграмму.
3. Построить СДНФ на основе следующего алгоритма
3.1. Выделить комбинации в таблице истинности, на которых функция равна 1.
3.2. Для каждой выделенной комбинации составить логическое произведение независимых переменных, из которых она образована, причем если в комбинации значение переменных равно 0, то в логическое произведение эта переменная входит с инверсией, если в комбинации значение переменной равно 1, то в логическое произведение эта переменная входит без инверсии.
3.3. Формула функции образуется путем логического сложения полученных логических произведений.

Теория дискретных устройств
4. Построить СКНФ на основе следующего алгоритма
4.1. Выделить комбинации в таблице истинности, на которых функция равна 0.
4.2. Для каждой выделенной комбинации составить логическое сложение независимых переменных, из которых она образована, причем если в комбинации значение переменных равно 0, то в логическое сложение эта переменная входит без инверсии, если в комбинации значение переменной равно 1, то в логическое произведение эта переменная входит с инверсией.
4.3. Формула функции образуется путем логического умножения полученных логических сложений.
5. Минимизация полученной логической функции в соответствии с тождествами, свойствами и законами алгебры логики (см. Приложения 3, 4, 5).
5.1. Минимизировать полученную СДНФ с помощью любых изученных свойств, тождеств и законов алгебры логики, полученный результат проверить.
5.2. Минимизировать полученную СКНФ с помощью любых изученных свойств, тождеств и законов алгебры логики, полученный результат проверить.

Теория дискретных устройств
6. Минимизация полученной логической функции с помощью карты Карно.
6.1. Составить карту Карно в дизъюнктивной форме для логической функции заданной в индивидуальном задании.
6.2. Выполнить минимизацию дизъюнктивной формы логической функции (получить МДНФ) по карте Карно.
6.3. Составить карту Карно в конъюнктивной форме для логической функции заданной в индивидуальном задании.
6.4. Выполнить минимизацию конъюнктивной формы логической функции (получить МКНФ) по карте Карно.

Теория дискретных устройств
Пример выполнения работы
f={1, 4, 5, 7}x,y,z
Исходные данные:
Составим таблицу истинности заданной функции:
На наборах аргументов 1, 4, 5, 7 функция f принимает значения 1. Следовательно, на наборах 0, 2, 3, 6 ‒ значения 0.

Теория дискретных устройств
Представление логической функции временной диаграммой

Теория дискретных устройств
Построение СДНФ заданной логической функции
Упрощение логической функции алгебраическим методом
Закон склеивания
Идемпотентный закон

Теория дискретных устройств
Проверка полученной МДНФ заданной логической функции путем подстановки значений переменных из таблицы истинности

Теория дискретных устройств
Закон склеивания
Идемпотентный закон
Построение СКНФ заданной логической функции

Теория дискретных устройств
Проверка полученной МКНФ заданной логической функции путем подстановки значений переменных из таблицы истинности

Теория дискретных устройств
Минимизация логических функций с помощью карт Карно
Минимизация СДНФ заданной логической функции методом Карно
1
1
1
1
ДФ

Теория дискретных устройств
Минимизация СКНФ логических функций методом Карно
0
0
КФ
0
0

Теория дискретных устройств
Приложение 1

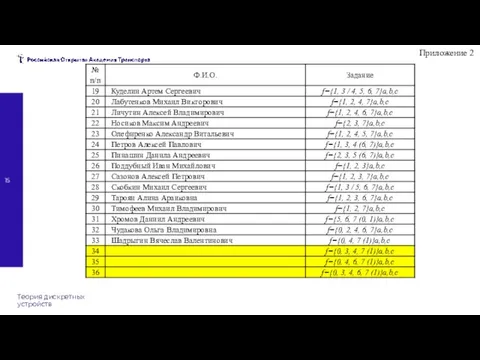
Теория дискретных устройств
Приложение 2

Теория дискретных устройств
Свойства
и отношения эквивалентности
Принцип подстановки
Симметричность
Транзитивность
Если x = y, то в любом выражении содержащем
переменную x, его можно заменить на переменную y
Если x = y, то и y = x
Если x = y и y = z, то x = z
Приложение 3

Теория дискретных устройств
Тождества алгебры логики
ИЛИ
НЕ
И
Приложение 4

Теория дискретных устройств
Законы алгебры логики
Коммутативный (переместительный)
Ассоциативный (сочетательный)
Дистрибутивный (распределительный)
Приложение 5
Идемпотентный