Содержание
- 2. ЦЕЛИ РАБОТЫ: уточнить понятие площади, выяснить историю вопроса, выстроить теорию «площади фигур» на основе площади треугольника,
- 3. УТОЧНЕНИЕ ПОНЯТИЯ ПЛОЩАДИ Опр. 1. Фигура называется простой, если она разбивается на конечное число плоских треугольников.
- 4. ИСТОРИЯ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ Понятия площадей прямолинейных фигур (треугольника, прямоугольника, параллелограмма и трапеции) являются самыми древними в
- 5. Основоположники геометрии. Математические труды. При доказательстве теорем о площадях фигур, ограниченных кривыми линиями, Архимед постоянно использует
- 6. Основоположники геометрии. Автор труда «Начала» в 13 книгах, в котором изложены основы геометрии, теории чисел, метод
- 7. Основоположники геометрии. Дал систематическое изложение основных достижений античности в математике и механике. Нашел формулы для определения
- 8. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА Поскольку фигура называется простой, если она разбивается на
- 9. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА 1. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА. Так как площадь
- 10. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА Нетрудно доказать, что с увеличением одного из катетов в а раз площадь
- 11. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА Тогда площадь произвольного треугольника будет равна сумме площадей двух прямоугольных треугольников, на
- 12. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА 2. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА равна сумме площадей двух равных
- 13. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА 3. ПЛОЩАДЬ ТРАПЕЦИИ равна сумме площадей треугольников с
- 14. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА 4. ПЛОЩАДЬ МНОГОУГОЛЬНИКА (выпуклого) равна сумме площадей треугольников,
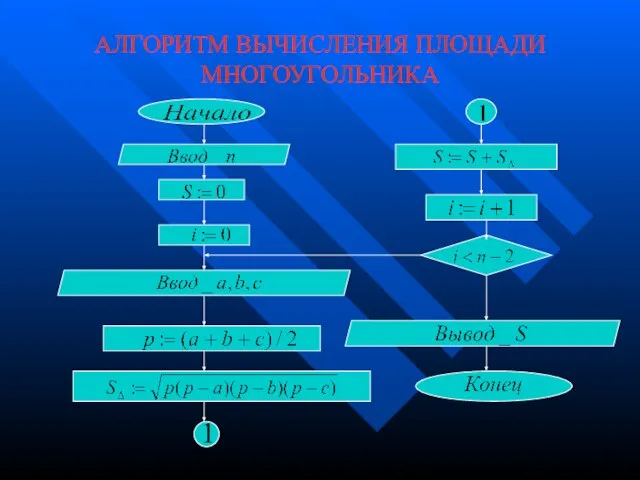
- 15. АЛГОРИТМ ВЫЧИСЛЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА
- 16. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Треугольник где a, b, c – стороны треугольника, р – полупериметр, r
- 17. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Параллелограмм Формулы площади ромба видоизменяются по сравнению с формулами площади параллелограмма в
- 18. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Трапеция Произвольный четырехугольник где d – диагональ трапеции (четырехугольника).
- 19. А КАК ПОСТУПИТЬ С КРУГОМ? Круг не является простой фигурой, поэтому формула его площади имеет иррациональное
- 20. СЛЕДУЕТ ОТДАТЬ ДОЛЖНОЕ ДРЕВНЕГРЕЧЕСКИМ МАТЕМАТИКАМ!
- 21. МЫ ХОДИМ ПО ПЛОЩАДЯМ Над программой работали: ⮚ 1-я гр. Понятие площади (Макаров А.). ⮚ 2-я
- 23. Скачать презентацию



















 Разложение многочленов на множители
Разложение многочленов на множители Презентация на тему Внутреннее строение Cолнца
Презентация на тему Внутреннее строение Cолнца  Раздел 1. Общая психология_Лекция 1_Психология как наука
Раздел 1. Общая психология_Лекция 1_Психология как наука Эволюция приматов 9 класс
Эволюция приматов 9 класс Тыва тоннарның хевирлери болгаш шын адаары
Тыва тоннарның хевирлери болгаш шын адаары Подготовка к ГИА с использованием ИКТ
Подготовка к ГИА с использованием ИКТ Презентация на тему Музыкальная драматургия - развитие музыки (7 класс)
Презентация на тему Музыкальная драматургия - развитие музыки (7 класс) Тема 7. Линейная модельпроизводственной структуры сельскохозяйственной организациина долгосрочную перспективу
Тема 7. Линейная модельпроизводственной структуры сельскохозяйственной организациина долгосрочную перспективу Клетка
Клетка Л.Н.Толстой Рассказ «После бала»
Л.Н.Толстой Рассказ «После бала» Проект
Проект Kursovaya_rabota
Kursovaya_rabota ГБУ ДО ДДЮ Приморского района
ГБУ ДО ДДЮ Приморского района Electronic Reserve System (eReserve)
Electronic Reserve System (eReserve) Доказательства происхождения классов позвоночных животных
Доказательства происхождения классов позвоночных животных Болезнь и синдром Рейно
Болезнь и синдром Рейно Модульные строительные конструкции на основе сталефибробетонной несъемной опалубки
Модульные строительные конструкции на основе сталефибробетонной несъемной опалубки Аппликация из крашеных опилок
Аппликация из крашеных опилок Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 1
Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 1 Ҡол Ғәли Йософ ҡиссаһы
Ҡол Ғәли Йософ ҡиссаһы Автоматизированная система пуска синхронных и асинхронных двигателей низкого и высокого напряжений
Автоматизированная система пуска синхронных и асинхронных двигателей низкого и высокого напряжений Декоративно-пркладное искусство России
Декоративно-пркладное искусство России Каркас унифицированный безригельный КУБ 2,5
Каркас унифицированный безригельный КУБ 2,5 Краткое описание. Бизнес проект по открытию ресторана фаст-фуд с последующим развитием сети. Рестораны фаст-фуд – предприятия общ
Краткое описание. Бизнес проект по открытию ресторана фаст-фуд с последующим развитием сети. Рестораны фаст-фуд – предприятия общ Презентация на тему Организация проектной деятельности учащихся на уроках биологии
Презентация на тему Организация проектной деятельности учащихся на уроках биологии  Государственный контроль за качеством образования
Государственный контроль за качеством образования Гражданин РФ
Гражданин РФ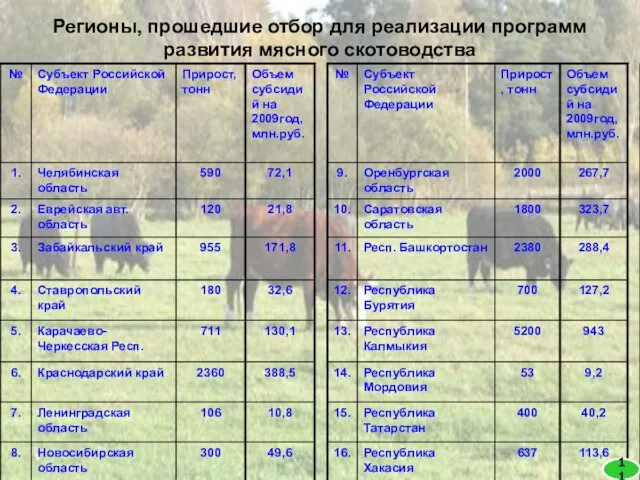 Регионы, прошедшие отбор для реализации программ развития мясного скотоводства
Регионы, прошедшие отбор для реализации программ развития мясного скотоводства