Содержание
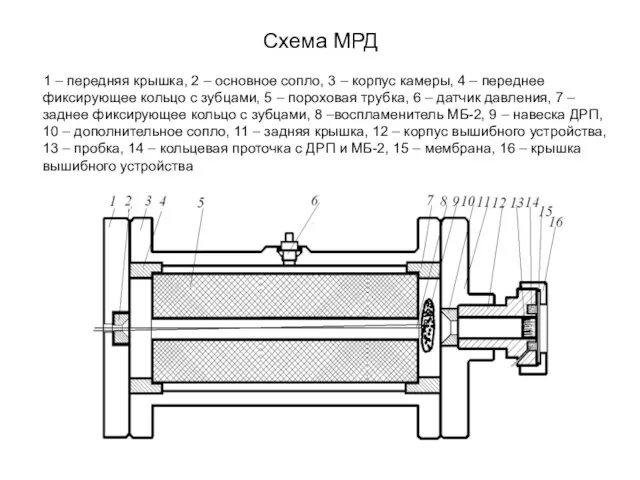
- 2. Схема МРД 1 – передняя крышка, 2 – основное сопло, 3 – корпус камеры, 4 –
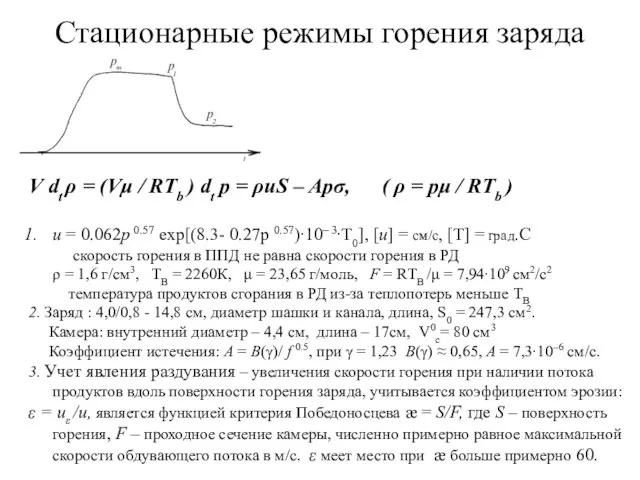
- 3. Стационарные режимы горения заряда V dt ρ = (Vμ / RTb ) dt p = ρuS
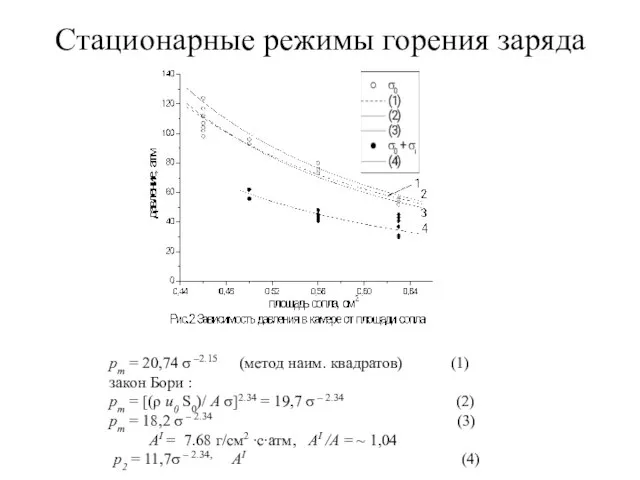
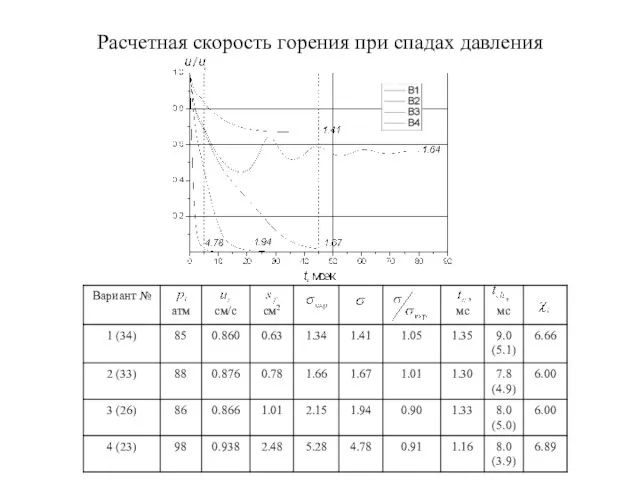
- 4. Стационарные режимы горения заряда рт = 20,74 σ –2.15 (метод наим. квадратов) (1) закон Бори :
- 5. ЭРОЗИОННОЕ ГОРЕНИЕ* В рамках представлений Я.Б. Зельдовича1 и исследований В.Н. Вилюнова2 увеличение скорости горения пороха при
- 6. Показано, что полученная формула хорошо описывает известные экспери-ментальные результаты при значениях α ≈ 0.005 ÷ 0.0065
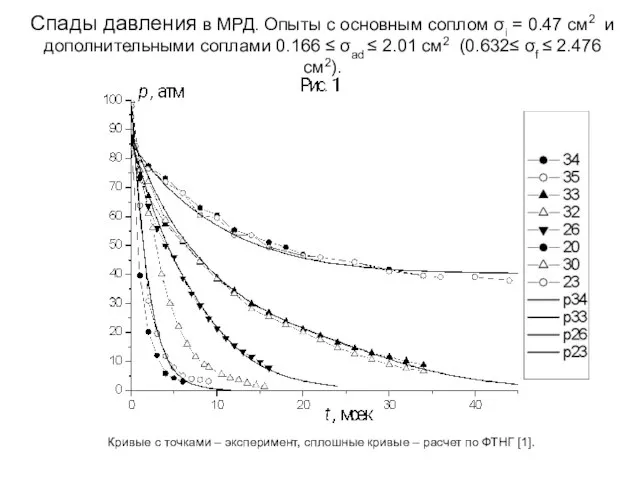
- 7. Спады давления в МРД. Опыты с основным соплом σi = 0.47 см2 и дополнительными соплами 0.166
- 8. Расчетная скорость горения при спадах давления
- 9. Обратная задача внутренней баллистики (ОЗВБ) T = const τch dt(p/pi) = u/ui - σ(p/pi) pV =
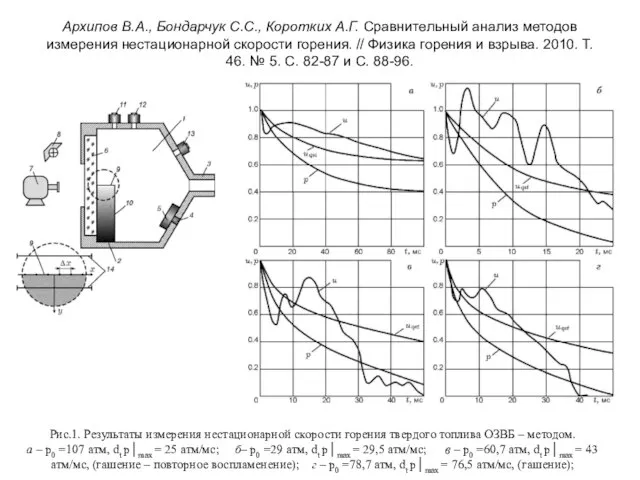
- 10. Архипов В.А., Бондарчук С.С., Коротких А.Г. Сравнительный анализ методов измерения нестационарной скорости горения. // Физика горения
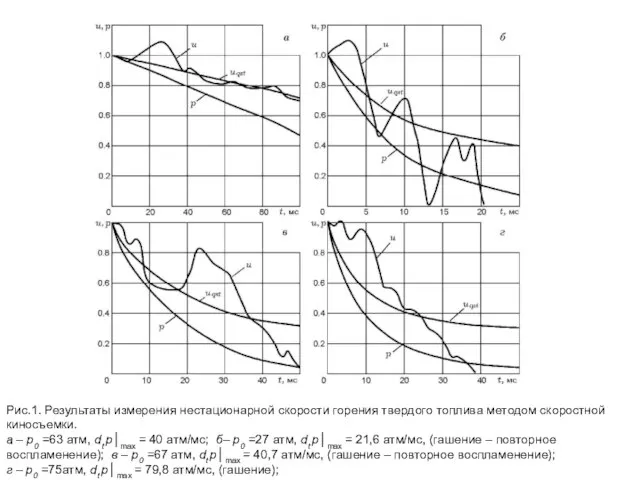
- 11. Рис.1. Результаты измерения нестационарной скорости горения твердого топлива методом скоростной киносъемки. а – р0 =63 атм,
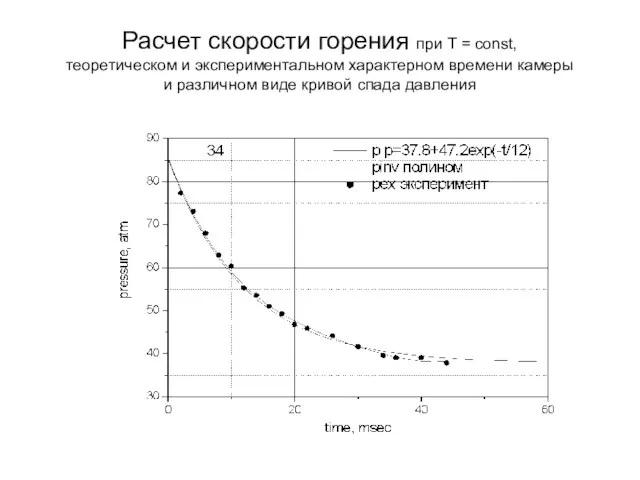
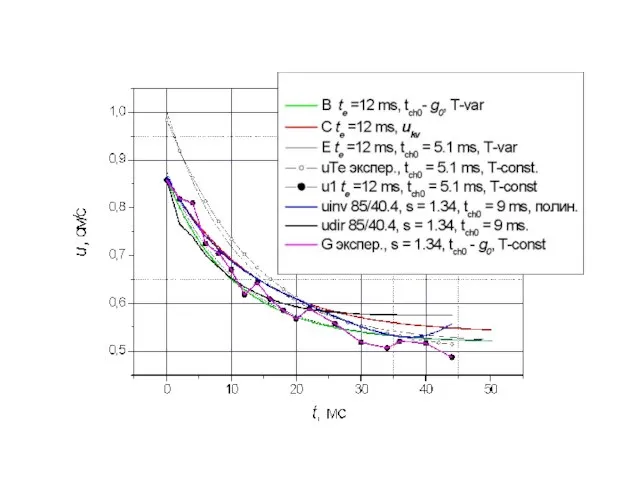
- 12. Расчет скорости горения при Т = const, теоретическом и экспериментальном характерном времени камеры и различном виде
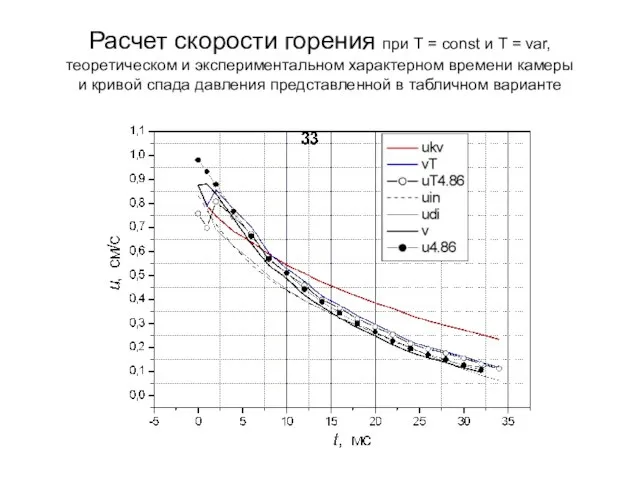
- 14. Расчет скорости горения при Т = const и Т = var, теоретическом и экспериментальном характерном времени
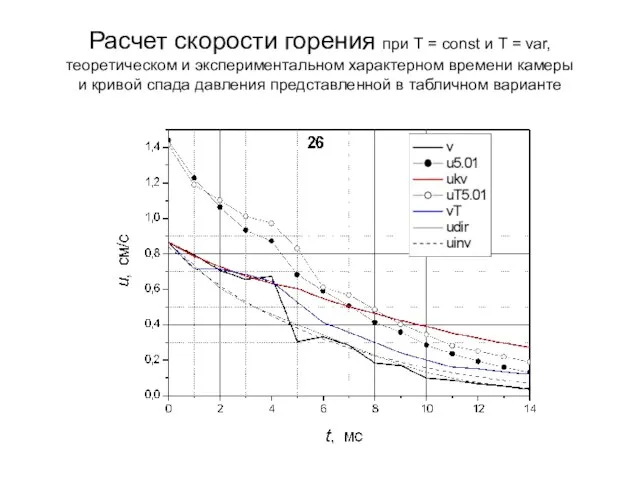
- 15. Расчет скорости горения при Т = const и Т = var, теоретическом и экспериментальном характерном времени
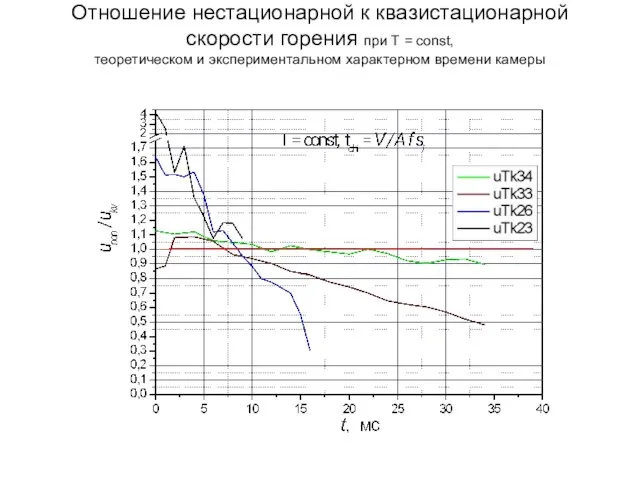
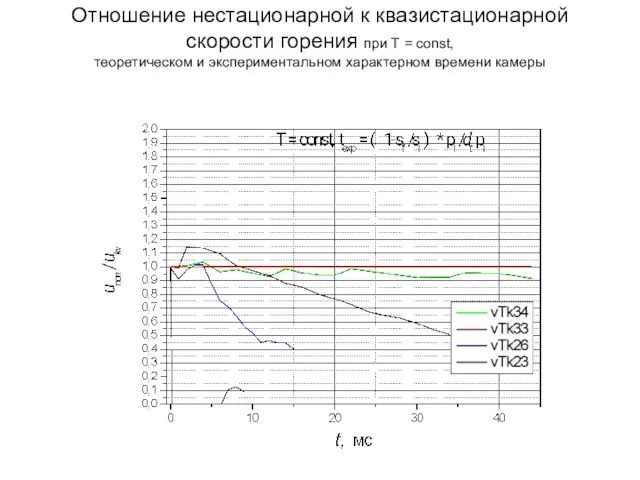
- 16. Отношение нестационарной к квазистационарной скорости горения при Т = const, теоретическом и экспериментальном характерном времени камеры
- 17. Отношение нестационарной к квазистационарной скорости горения при Т = const, теоретическом и экспериментальном характерном времени камеры
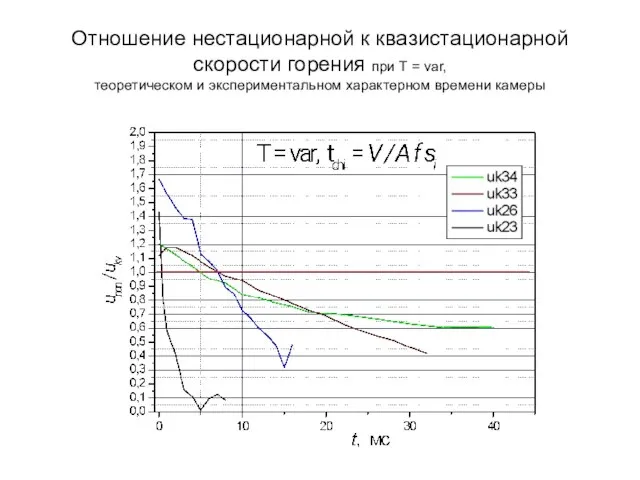
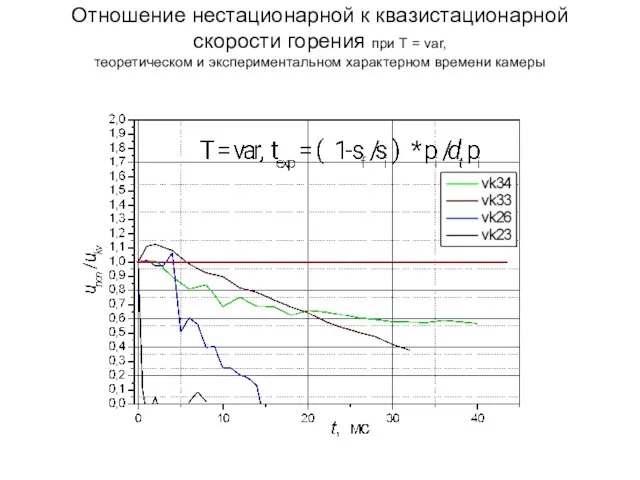
- 18. Отношение нестационарной к квазистационарной скорости горения при Т = var, теоретическом и экспериментальном характерном времени камеры
- 19. Отношение нестационарной к квазистационарной скорости горения при Т = var, теоретическом и экспериментальном характерном времени камеры
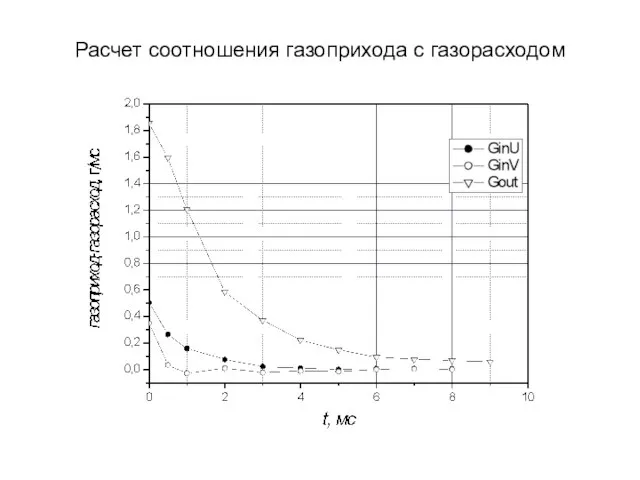
- 20. Расчет соотношения газоприхода с газорасходом
- 21. a b c d e Вид поверхностей горения: a –видеофильм, порох НБ, d = 12 мм,
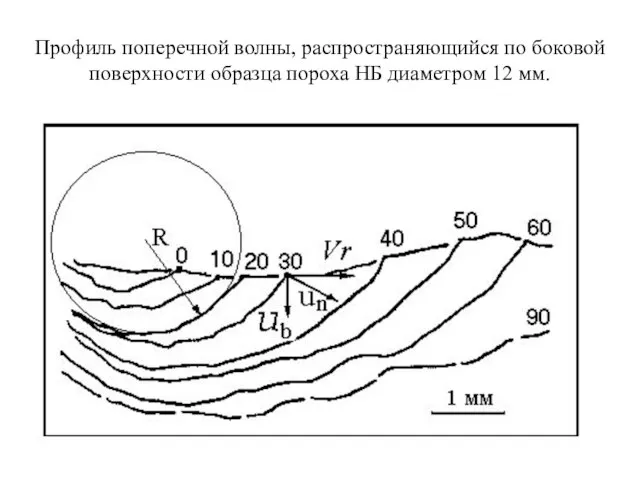
- 22. Профиль поперечной волны, распространяющийся по боковой поверхности образца пороха НБ диаметром 12 мм.
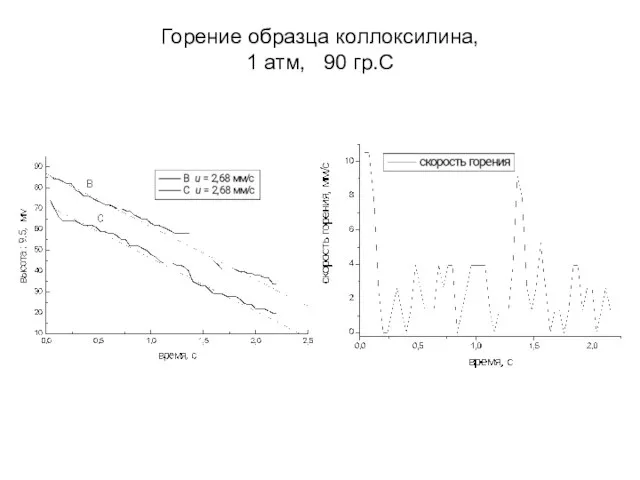
- 23. Горение образца коллоксилина, 1 атм, 90 гр.С
- 25. Скачать презентацию




 Органы путевой стабилизации и управления маневренных самолётов и беспилотных летательных аппаратов
Органы путевой стабилизации и управления маневренных самолётов и беспилотных летательных аппаратов Мультипликационные герои
Мультипликационные герои Всемирный день правовой помощи детям
Всемирный день правовой помощи детям Музыкальная живопись и живописная музыка
Музыкальная живопись и живописная музыка игра кузя
игра кузя game-4
game-4 Отчёт о работе отдела продаж за май
Отчёт о работе отдела продаж за май Акеда. Воля и попущение
Акеда. Воля и попущение Суффикс и его роль в слове
Суффикс и его роль в слове УФК по Оренбургской области Внедрение системы ключевых показателей эффективности исполнения бюджетов бюджетной системы Российс
УФК по Оренбургской области Внедрение системы ключевых показателей эффективности исполнения бюджетов бюджетной системы Российс Презентация на тему Изменчивость Мутации
Презентация на тему Изменчивость Мутации Основной закон - основа жизни
Основной закон - основа жизни ...В слове МЫ сто тысяч Я.
...В слове МЫ сто тысяч Я. Образ Екатерины II глазами историков, художников и писателей XVIII-XIX веков
Образ Екатерины II глазами историков, художников и писателей XVIII-XIX веков ФОРМИРОВАНИЕ ИНСТИТУТОВ РИСК-МЕНЕДЖМЕНТА В КОРПОРАЦИЯХ: ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ Роман Качалов ЦЭМИ РАН 07 апреля 2010 XI Международн
ФОРМИРОВАНИЕ ИНСТИТУТОВ РИСК-МЕНЕДЖМЕНТА В КОРПОРАЦИЯХ: ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ Роман Качалов ЦЭМИ РАН 07 апреля 2010 XI Международн Как начать спокойную жизнь, без мыслей о тревоге, панических атаках и страхах
Как начать спокойную жизнь, без мыслей о тревоге, панических атаках и страхах Из опыта работы по реализации программы математического кружка «Решение олимпиадных задач»
Из опыта работы по реализации программы математического кружка «Решение олимпиадных задач» ОБРЯДЫ И ВЕРОВАНИЯ, СВЯЗАННЫЕС ПОСТРОЙКОЙ И ЗАСЕЛЕНИЕМ ДОМА.ОБЕРЕГИ СЕВЕРНОЙ ИЗБЫ
ОБРЯДЫ И ВЕРОВАНИЯ, СВЯЗАННЫЕС ПОСТРОЙКОЙ И ЗАСЕЛЕНИЕМ ДОМА.ОБЕРЕГИ СЕВЕРНОЙ ИЗБЫ Так ли безобидна кнопка?
Так ли безобидна кнопка? День Героев Отечества
День Героев Отечества Баллада о влюбленном Павуке. Синопсис. Игра для одного человека
Баллада о влюбленном Павуке. Синопсис. Игра для одного человека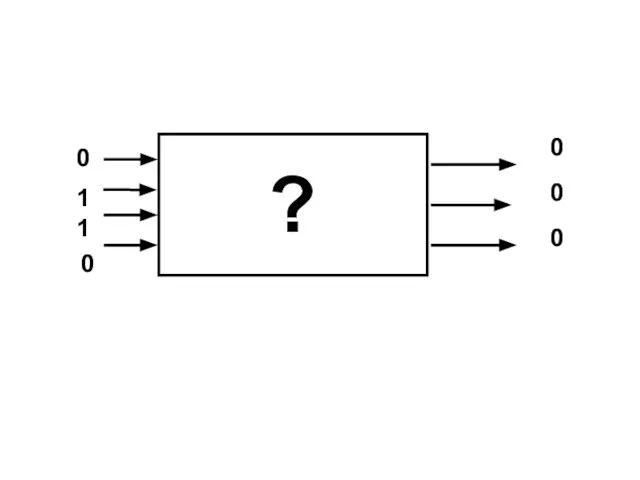 0 0 0 1 1 0 ? 01 1 0 1 1 0 ? 1Простое высказывание – повествовательное предложение, принимающее одно из двух возможных значений – истина или
0 0 0 1 1 0 ? 01 1 0 1 1 0 ? 1Простое высказывание – повествовательное предложение, принимающее одно из двух возможных значений – истина или  Унҗиденче март. Билгеле үткән заман хикәя фигыль
Унҗиденче март. Билгеле үткән заман хикәя фигыль Рельеф территории России
Рельеф территории России Динамика твердого тела
Динамика твердого тела 25 000 000 5 000 000 58% аудитории старше 25 лет TNS Web Index Report, сентябрь 2010.
25 000 000 5 000 000 58% аудитории старше 25 лет TNS Web Index Report, сентябрь 2010. Бизнес-планирование
Бизнес-планирование Институт филологии, иностранных языков и массовых коммуникаций
Институт филологии, иностранных языков и массовых коммуникаций