Содержание
- 2. 1. Решить уравнение √3sin2x+2cos2x–1=2sinx . 2. Найти множество значений функции y=cos3x-4sin3x+5. 3. Найти все значения «а»,
- 3. Применение свойств функций. Найти все значения «а», при которых уравнение 5x2-9cosx+a=0 имеет нечетное число корней. Четность
- 4. 2. Решить уравнения 2cosx/3=2x+2-x, б) sinx+sin5x=2. Ограниченность функций
- 5. Sin√x=-1/2 Cosx2=- √3/2
- 6. Решить уравнение Cosx·Cos2x ·Cos4x ·Cos8x=1/16 Упростить Sinπ/11·Sin3π/11·Sin5π/11·Sin7π/11·Sin9π/11 Формула двойного угла
- 7. Задача Тангенсы половин углов прямоугольного треугольника образуют арифметическую прогрессию. Найти углы треугольника.
- 9. Скачать презентацию



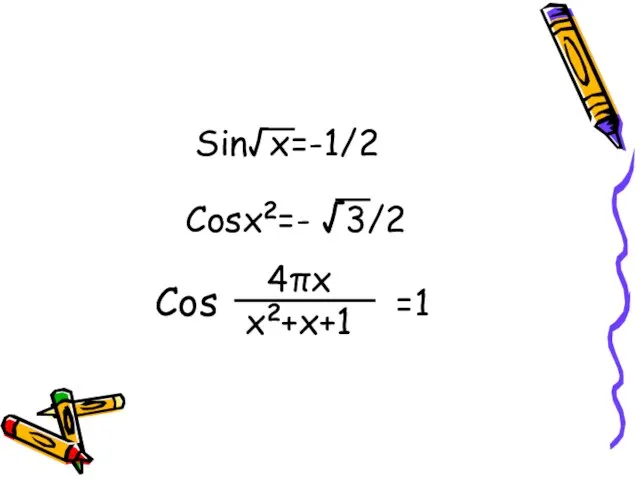


 История и концепция управления проектом
История и концепция управления проектом Чем известен Петербург? Тема 1
Чем известен Петербург? Тема 1 0be5ea2b5664ecf8
0be5ea2b5664ecf8 Презентация на тему Мойдодыр (1 класс)
Презентация на тему Мойдодыр (1 класс)  Эволюция официального исторического нарратива и политика идентичности в РФ
Эволюция официального исторического нарратива и политика идентичности в РФ История пасхального яйца
История пасхального яйца Исследовательская работа на тему «история моды»
Исследовательская работа на тему «история моды» Г
Г Житлово-побутовий відділ університету ім. О.О. Богомольця
Житлово-побутовий відділ університету ім. О.О. Богомольця Интеграция очных и дистанционных форм обучения для устойчивого развития
Интеграция очных и дистанционных форм обучения для устойчивого развития Исследование возможности переработки невостребованной древесины осины в товарный продукт
Исследование возможности переработки невостребованной древесины осины в товарный продукт Презентация на тему Развитие речи малыша в первый год жизни
Презентация на тему Развитие речи малыша в первый год жизни Системи лінійних алгебраичных рівнянь
Системи лінійних алгебраичных рівнянь  Temperament_i_kommunikatsia_Praktika_2
Temperament_i_kommunikatsia_Praktika_2 Презентация на тему Метеориты 5 класс
Презентация на тему Метеориты 5 класс Harry Houdini (1874–1926)
Harry Houdini (1874–1926) Комплексный план модернизации моногорода Сокола Вологодской области
Комплексный план модернизации моногорода Сокола Вологодской области Творческий проект
Творческий проект Летний костюм
Летний костюм Музей-усадьба И.С. Тургенева «Спасское-Лутовиново»
Музей-усадьба И.С. Тургенева «Спасское-Лутовиново» ОГЭ 2016
ОГЭ 2016 Презентация без названия
Презентация без названия British Meals and Meal Times in Britain
British Meals and Meal Times in Britain Свет. Характеристики света
Свет. Характеристики света Факторы, влияющие на скорость химической реакции
Факторы, влияющие на скорость химической реакции Оптимизация бюджета капиталовложений
Оптимизация бюджета капиталовложений Числовые суеверия
Числовые суеверия Презентация на тему Электромагнетизм
Презентация на тему Электромагнетизм