НОД И НОК ЧИСЕЛ

НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
Наибольшее натуральное число на которое де-лятся без остатка числа a и b, называют наи-большим общим делителем чисел a и b.
Например: НОД чисел 48 и 36 равен 12, т.е. наи-
большему из натуральных чисел, ко-
торое делит нацело и 48, и 36.
НОД(48;36)=12.

ПОМНИ!
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
разложить их на простые множители;
из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
найти произведение оставшихся множителей.
Например: НОД (96, 72)=24
96=2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3, 72=2 ∙ 2 ∙ 2 ∙ 3 ∙ 3
Остались множители: 2 ∙ 2 ∙ 2 ∙ 3=24.

ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№1. Найдите НОД чисел: а)108 и 72; б) 150 и 225 .
Решение. Разложим числа на простые множители:
108 2 72 2 150 2 225 5
54 2 36 2 75 5 45 5
27 3 18 2 15 5 9 3
9 3 9 3 3 3 3 3
3 3 3 3 1 1 1 1
1 1
Найдем одинаковые множители ( выделены одним цветом)
НОД(108; 72) = 36, т.к. НОД(150; 225) = 75, т.к.
2 ∙ 2 ∙ 3 ∙ 3 = 36. 5 ∙ 5 ∙ 3 = 75.

Числа
правят миром.
Пифагор
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
ВЗАИМНО ПРОСТЫЕ ЧИСЛА
Найти наибольший общий делитель чисел:
а) 22 и 39; б) 56 и 31; в) 73 и 45; г) 44 и 63.
Если вы решали все примеры верно, то в ответе
всегда получалась 1.

НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Наименьшим общим кратным натуральных чи-сел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Например: НОК чисел 75 и 60 равен300, т.е. наименьшему из натуральных чисел, которые
делятся без остатка на числа 75 и 60.
НОК(75 и 60) =300

ПОМНИ!
Чтобы найти наименьшее общее кратное несколь-
ких натуральных чисел , надо:
разложить их на простые множители;
выписать множители, входящие в разложение
одного из чисел;
добавить к ним недостающие множители из
разложений остальных чисел;
найти произведение получившихся множите-
лей.

∙
ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№2. Найдите НОК чисел: а) 108 и 72; б) 150 и 225.
Решение. Разложим числа на простые множители:
108 2 72 2 150 2 225 5
54 2 36 2 75 5 45 5
27 3 18 2 15 5 9 3
9 3 9 3 3 3 3 3
3 3 3 3 1 1
1 1
НОК(150; 225) = 5 ∙ 5 ∙ 3 ∙ 3 ∙ 2 = 450
НОК(108; 72) = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 2 = 216

РЕШИ САМОСТОЯТЕЛЬНО
№1.Найдите:
а) НОД (81 и 243) б) НОК(15 и 18)
в) НОД(72 и 108) г) НОК(36 и 48)
д) НОД(168 и 180) е) НОК(252 и 360)
ж) НОД(360 и 1050) з) НОК(396 и 180)
и)НОД(270;450 и 555) к) НОК(72;120 и 264)

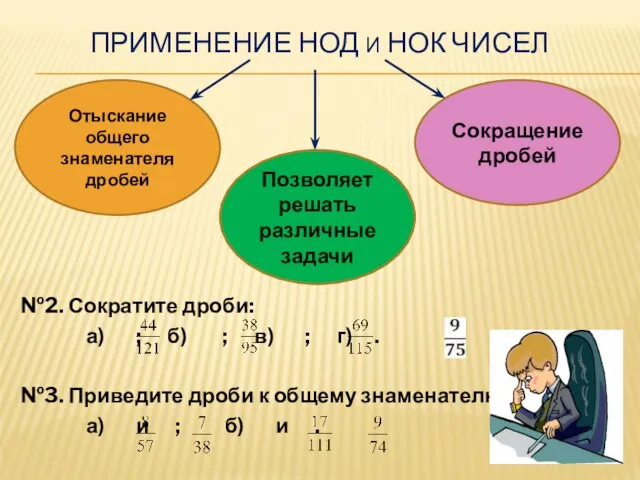
Позволяет
решать
различные
задачи
Сокращение
дробей
Отыскание общего
знаменателя
дробей
ПРИМЕНЕНИЕ НОД И НОК ЧИСЕЛ
№2. Сократите дроби:
а) ; б) ; в) ; г) .
№3. Приведите дроби к общему знаменателю:
а) и ; б) и .

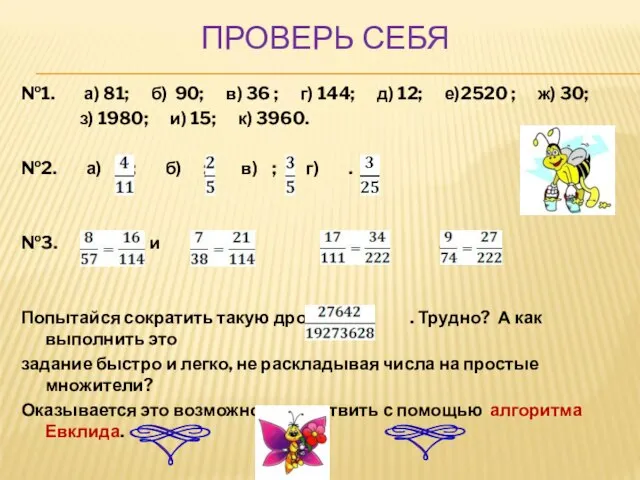
ПРОВЕРЬ СЕБЯ
№1. а) 81; б) 90; в) 36 ; г) 144; д) 12; е)2520 ; ж) 30;
з) 1980; и) 15; к) 3960.
№2. а) ; б) ; в) ; г) .
№3. и ; и .
Попытайся сократить такую дробь: . Трудно? А как выполнить это
задание быстро и легко, не раскладывая числа на простые множители?
Оказывается это возможно осуществить с помощью алгоритма Евклида.

АЛГОРИТМ ЕВКЛИДА
Во многих случаях, когда числитель и знаменатель делятся на число (например на 19, на 37 и т.д.), а признака делимости мы не знаем, НОК числителя и знаменателя находят с помо-щью, так называемого, алгоритма Евклида.
Суть его проста: делится большее число на меньшее. Затем меньшее делится на первый остаток. При этом получается второй остаток. Дальше первый остаток делится на второй и процесс продолжается. Он конечен и последний неравный нулю остаток и будет наибольший общим делителем. Прием этот занимателен, он называется –алгоритм Евклида – реко-мендуем его испробовать.
Продемонстрируем его на примере.

СОКРАТИТЬ ДРОБЬ: .
Для того, чтобы сократить данную дробь найдем с помощью алгоритма Евкли-
да НОД чисел 5959 и 13433. Делим 13433 на 5959.
13433 5959
11918 2
5959 1515
4545 3
1515 1414
1414 1
1414 101
101 14
404 =
404
0
Последний неравный нулю остаток, т.е. 101 и будет наибольшим общим дели-
телем. Разделим на 101 числитель и знаменатель. Получим дробь: .

РЕШИ САМОСТОЯТЕЛЬНО
№1. С помощью алгоритма Евклида сократить дроби:
а) б) в) г) д)
; ; ; ; .
№2. Найдите НОД чисел:
а) 2304 и 5220; б) 8136 и 12250; в) 1348 и 1126;
г) 42628 и 33124; д) 71004 и 154452.
№3. Какой наименьшей длины должна быть доска, чтобы ее можно было раз-
резать поперек на части, равные 20см и 27см, не получив обрезков?
№4. Какое наибольшее число одинаковых комплектов можно составить из
елочных игрушек, если имеется 12 зайцев, 24 лисицы, 16 морковок и 48
яблок?
№5. Найдите НОК и НОД чисел, затем сравните произведение этих чисел с
произведением НОК и НОД:
а) 14 и21; б) 24 и 36; в) 32 и 48; г) 18 и24; д) 25 и 35.

РЕШАЕМ И ПРОВЕРЯЕМ
№1.
№2.
№3.
№4.
№5.
а) НОД (14; 21) = 7; б) НОД (24; 36) = 12;
НОК (14; 21) = 42. НОК (24; 36) = 72.
в) НОД (32; 48) = 16; г) НОД (18; 24) = 6;
НОК (32; 48) = 96. НОК (18; 24) = 72.
д) НОД (25; 35) = 5;
НОК (25; 35) =175.

ЗАМЕЧАТЕЛЬНОЕ СВОЙСТВО НОК И НОД
Заметили ли вы, что для любых натуральных чисел a и b выпол-
няется равенство:
НОД(a;b) НОК(a;b) = a b
Это свойство позволяет по заданным числам и известному НОД
находить НОК этих чисел.
a b
НОК(a;b) =
НОД(a;b)

ПРЕДЛАГАЮ РЕШИТЬ ЗАДАЧИ
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в коробке. Какое наименьшее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну?
Какое наибольшее число одинаковых подарков можно составить из 48 конфет "Ласточка" и 36 конфет "Белочка", если надо использовать все конфеты? Сколько конфет "Ласточка" и "Белочка" будет в каждом подар-ке?
Для поездки за город работникам завода было выделено несколько ав-тобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а кон-феты «Геометрия с орехами» – по 15 штук в коробке. Какое наимень-шее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну?
Коля, Серёжа и Ваня регулярно ходили в кинотеатр. Коля бывал в нём каждый 3-й день, Серёжа — каждый 7-й, Ваня — каждый 5-й. Сегодня все ребята были в кино. Когда все трое встретятся в кинотеатре в сле-дующий раз?