Содержание
- 2. Производная и интеграл В конце 17 века в Европе образовались две крупные математические школы. Главой одной
- 3. Происхождение производной Ряд задач дифференциального исчисления был решен еще в древности. Такие задачи можно найти у
- 4. Происхождение производной Ньютон пришел к понятию производной, исходя из вопросов механики. Свои результаты в этой области
- 5. Портрет Ньютона художника Русакова. Мы видим фундаментальной труд «Математические начала натуральной философии», в котором Ньютон изложил
- 6. Фундаментальный труд Ньютона «Математические начала натуральной философии» (в современном переводе «Математические основы физики») был издан в
- 7. Был летний день. Исаак Ньютон любил размышлять, сидя в саду, на открытом воздухе. Предание сообщает, что
- 8. Первые научные опыты Ньютона связаны с исследованиями света. В результате многолетней работы Исаак Ньютон установил, что
- 9. Бином Ньютона Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух
- 10. Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты,
- 11. Бином Ньютона в литературе В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь
- 12. Происхождение производной В подходе Лейбница к математическому анализу были некоторые особенности. Лейбниц мыслил высший анализ не
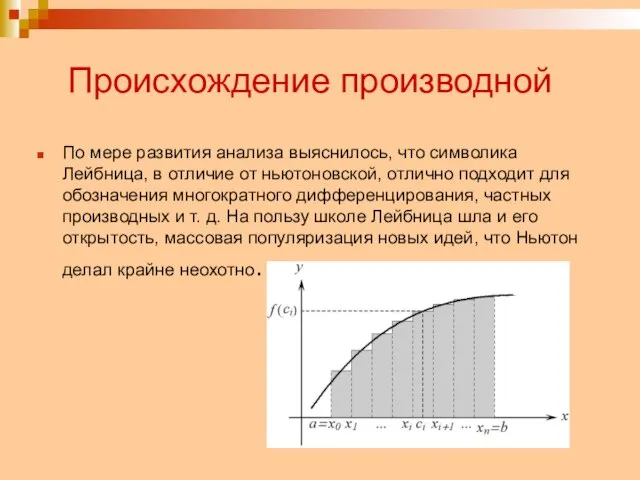
- 13. Происхождение производной По мере развития анализа выяснилось, что символика Лейбница, в отличие от ньютоновской, отлично подходит
- 14. Работы Лейбница по математике многочисленны и разнообразны. В 1666 года он написал первое сочинение: «О комбинаторном
- 15. Кто автор производной? Ньютон создал свой метод, опираясь на прежние открытия, сделанные им в области анализа,
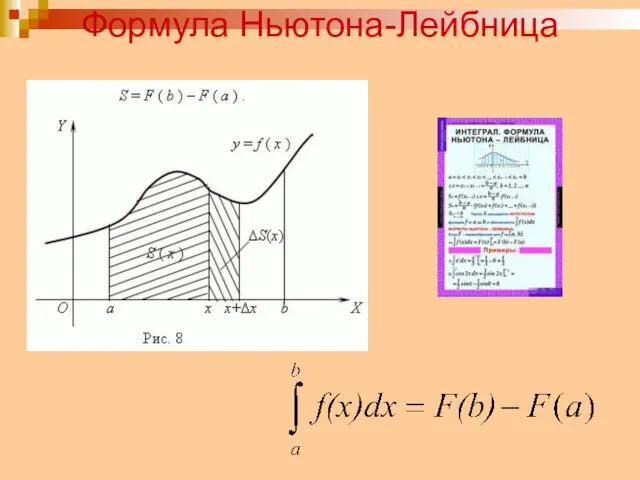
- 16. Формула Ньютона-Лейбница
- 18. Памятник Ньютону в Кэмбридже.
- 19. Памятник Лейбницу в Лейпциге.
- 23. Использованные ресурсы: http://ru.wikipedia.org/wiki/Лейбниц,_Готфрид_Вильгельм http://www.aphorisme.ru/about-authors/leybnic/?q=3519 http://www.fmclass.ru/math.php?id=484121ce1c9d1 http://todayinsci.com/L/Leibniz_Gottfried/LeibnizGottfried-Quotations.htm http://sat24.ucoz.ru/forum/82-101-2 http://www.dentmaster.ru/node/8060?size=preview http://ru.picscdn.com/domain/benisrael.net/ http://post.kards.qip.ru/compose/edit/ньютон/9471809/2/njuton_pod_jablonej.htm http://www.people.su/32/r1http://www.people.su/32/r1http://lib.rus.ec/b/259787/read http://www.help-rus-student.ru/pictures_fail/54/263_2.htm http://sokemem.com/review/books-by-isaac-newtonhttp://sokemem.com/review/books-by-isaac-newtonhttp://www.math.spbu.ru/user/jvr/DA_html/_lec_1_04.html http://www.infanata.com/page/621/ http://www.lib.vitebsk.net/libs/11/41/ http://chtiva.net/лейбниц/
- 24. Использованные ресурсы: http://www.alib.ru/bs.php4?uid=1129dbb67b5eacfb00831c58dd512a88c759 http://www.dom-knigi.ru/book.asp?Art=316871&CatalogID=158 http://www.athens.kiev.ua/lejbnic/ http://www.100book.ru/predel_funkcij_formuly_nyutona-lejbnica_i_tejlora_b382187.html http://tvsh2004.narod.ru/ma_12-0.htm Мордкович А.П. П.В.Алгебра и начала анализа (профильный уровень) 10
- 26. Скачать презентацию





















 Предложение по перспективному развитию военного городка отдельного медико-санитарного батальона г. Балашиха
Предложение по перспективному развитию военного городка отдельного медико-санитарного батальона г. Балашиха Язык современной Интернет - субкультуры
Язык современной Интернет - субкультуры Отцовская доблесть. Семья Канчуриных
Отцовская доблесть. Семья Канчуриных Кто хочет стать миллионером (разовая игра 15 вопросов)
Кто хочет стать миллионером (разовая игра 15 вопросов) Публичный отчет МОУ СОШ №18 г. Пензы (декабрь 2009 г.)
Публичный отчет МОУ СОШ №18 г. Пензы (декабрь 2009 г.) Презентация на тему Декартовы координаты
Презентация на тему Декартовы координаты  Кулинарные традиции семьи
Кулинарные традиции семьи Аксонометрия. Прямоугольные и косоугольные аксонометрические проекции
Аксонометрия. Прямоугольные и косоугольные аксонометрические проекции Технические средства измерения массы груза
Технические средства измерения массы груза Мой любимый продукт
Мой любимый продукт Гамма-стерилизация
Гамма-стерилизация Химическое оружие. Виды
Химическое оружие. Виды ОРГАНИЗАЦИЯ ПРОЦЕССА ОБУЧЕНИЯ В ПОЛЬШЕ
ОРГАНИЗАЦИЯ ПРОЦЕССА ОБУЧЕНИЯ В ПОЛЬШЕ Служба в органах уголовно-исполнительной системы как вид государственной службы
Служба в органах уголовно-исполнительной системы как вид государственной службы Путевая бюрократия или все о вагонной документации
Путевая бюрократия или все о вагонной документации Ecological problems
Ecological problems Продам 2 комнатную квартиру по приятной цене
Продам 2 комнатную квартиру по приятной цене Возрастная психология
Возрастная психология Правила vs Нормы
Правила vs Нормы Психолог-юзабилист О новой профессии в мире высоких технологий (для студентов-психологов)
Психолог-юзабилист О новой профессии в мире высоких технологий (для студентов-психологов) Управления рисками в банке
Управления рисками в банке Презентация на тему Мировые религии
Презентация на тему Мировые религии Ядерная сделка с Ираном
Ядерная сделка с Ираном Lean Startup «Бережливый стартап» Как делать игры, нужные людям
Lean Startup «Бережливый стартап» Как делать игры, нужные людям Презентация на тему Первые летательные аппараты
Презентация на тему Первые летательные аппараты Документирование среды программирования для операционной системы L4Ka(Documenting the programmer environment for L4ka)
Документирование среды программирования для операционной системы L4Ka(Documenting the programmer environment for L4ka) Правописание частицы НЕ с глаголами
Правописание частицы НЕ с глаголами Пьеса для театра А.Н.Островского "Снегурочка"
Пьеса для театра А.Н.Островского "Снегурочка"