О теоретической интерпретации данных RHIC.

Содержание:
Введение.
Ядерное экранирование кварков и глюонов.
Инклюзивные спектры в ядерных взаимодействиях.
Анизотропные потоки.
Рождение J/ψ–мезонов.
Заключение.

Введение.
Наличие фазового перехода конфайнмент – деконфайнмент в КХД.
Фазовая диаграмма.
Столкновения тяжелых ионов при высоких энергиях – способ изучения
адронной материи в экстремальных условиях при температуре Т > Tc
в фазе деконфайнмента :
кварк-глюонной плазмы (КГП).

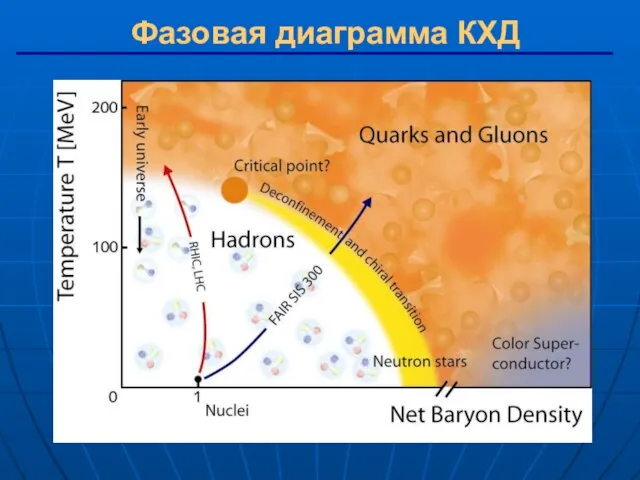
Фазовая диаграмма КХД

Столкновения тяжелых ионов и КГП.
В последние годы (в основном благодаря данным RHIC ) представления о КГП изменились.
Если раньше КГП рассматривалась
как газ кварков и глюонов, то сейчас - как (почти идеальная) жидкость,КГПс (QGPs). Сильное взаимодействие между кварками и глюонами является естественным при Т ~ 200 Мэв ~ ΛQCD.
Важная роль непертурбативных эффектов

Столкновения тяжелых ионов и КГП.
При исследовании ядро-ядерных взаимодействий возникает ряд
важных вопросов:
а) Каковы адекватные степени свободы?
б) Какова пространственно-временная картина?
в) Кварк-глюонная структура сталкивающихся ядер.
г) Достигается ли равновесие в процессе?
д) Сколько времени существует КГП?
е) Характерные сигналы КГП?

Пространственно-временная картина взаимодействий при высоких энергиях.
Большая длина когерентности (время) адронных флуктуаций
Δt ~ 2p/(M-m)
При высоких энергиях адронные (ядерные) флуктуации «приготавливаются» задолго до взаимодействия.
Какова структура фоковских состояний адронов (ядер) в СБИ?
Важную роль играют медленные партоны с долей импульса x << 1/mN RA.

Пространственно-временная картина взаимодействий при высоких энергиях.
Медленные партоны разных нуклонов ядра (с близкими прицельными параметрами) перекрываются и взаимодействуют.
В результате их плотность уменьшается и в пределе сверхвысоких энергий (или при А ?∞) возникает «насыщение».
Расчеты глюонной компоненты ядер в пределе «насыщения» проводились на основе теории возмущений КХД.
”Color glass condensate” (CGC) L.McLerran et al

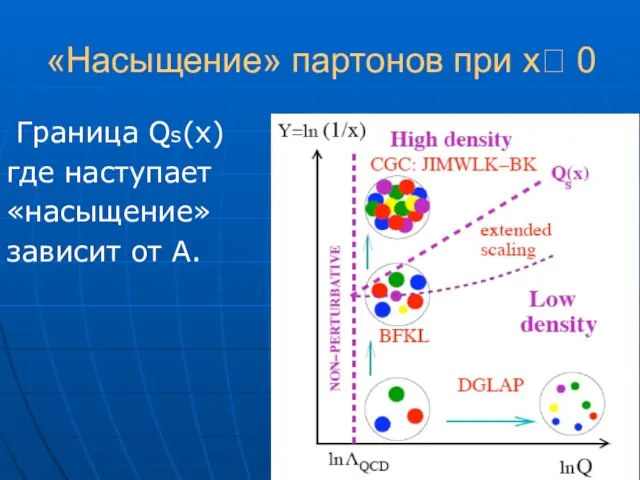
«Насыщение» партонов при х? 0
Граница Qs(х)
где наступает
«насыщение»
зависит от А.

Пространственно-временная картина взаимодействий при высоких энергиях.
Пространственно-временная картина hA (AB) –взаимодействий изменяется при энергии Ec когда lcoh ~ Δt ~ RA.
Для типичных взаимодействий Ec ~ mNRA.
При E < Ec амплитуда упругого hA – рассеяния возникает за счет последовательных перерассеяний
начального адрона
на нуклонах ядра
(модель Глаубера).

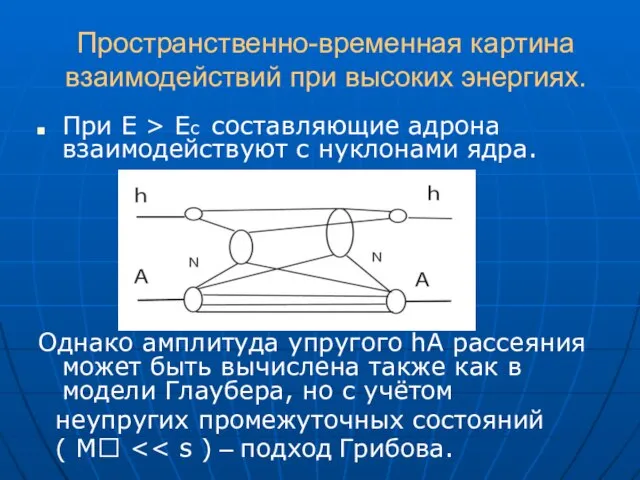
Пространственно-временная картина взаимодействий при высоких энергиях.
При E > Ec составляющие адрона взаимодействуют с нуклонами ядра.
Однако амплитуда упругого hA рассеяния может быть вычислена также как в модели Глаубера, но с учётом
неупругих промежуточных состояний
( M << s ) – подход Грибова.

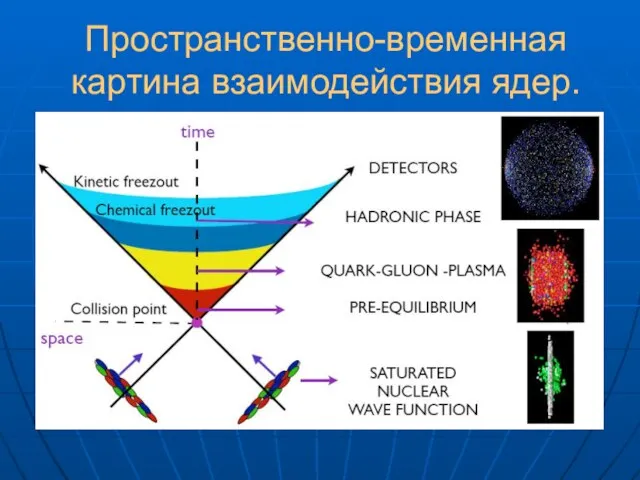
Пространственно-временная картина взаимодействия ядер.

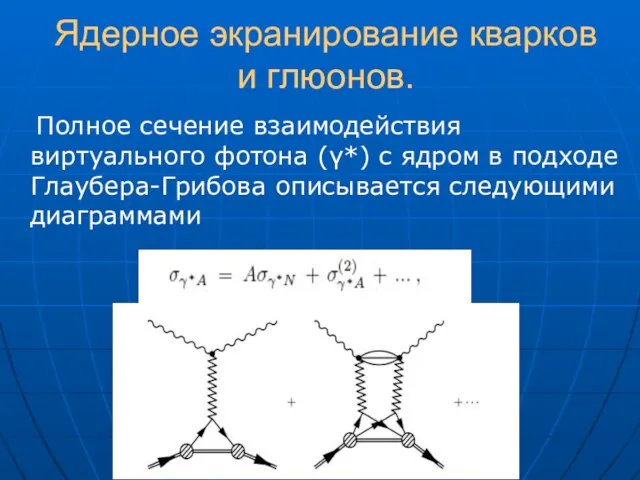
Ядерное экранирование кварков и глюонов.
Полное сечение взаимодействия виртуального фотона (γ*) с ядром в подходе Глаубера-Грибова описывается следующими диаграммами

Вклад второго перерассеяния
где
Продольная часть ядерного форм-фактора
Учитывает условие когерентности:
x<< 1/mN RA

Многократные перерассеяния.
Поправки более высоких порядков – модельно зависимы. Две модели, использовавшиеся в работах
A.Capella et al (1997),N.Armesto et al (2003), K.Tywoniuk et al(2006) :
a) Модель Швиммера
где

Многократные перерассеяния.
b) Модель квази-эйконала
Отношение сечений на нуклон для различных ядер
В модели Швиммера

Дифракционное рождение в γ*p-столкновениях.
Для вычисления ядерного экранирования в этом подходе необходимо знать соответ-
ствующие сечения дифракционной диссоциации на нуклоне.
В работе A.Capella et al для описания ядерных структурных функций в области малых х (экранирование кварков) использовалась параметризация данных HERA (с учётом КХД-эволюции).

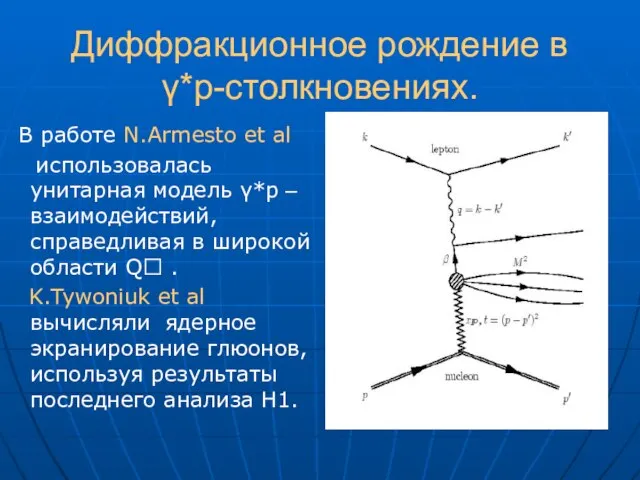
Диффракционное рождение в γ*p-столкновениях.
В работе N.Armesto et al
использовалась унитарная модель γ*p –взаимодействий, справедливая в широкой области Q .
K.Tywoniuk et al вычисляли ядерное экранирование глюонов, используя результаты последнего анализа H1.

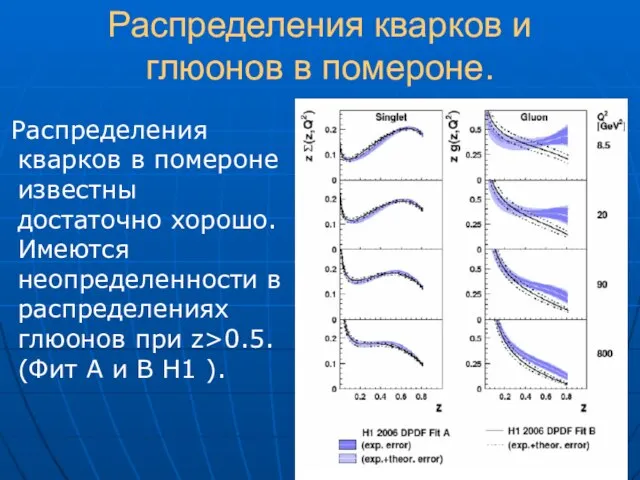
Распределения кварков и глюонов в помероне.
Распределения кварков в помероне известны достаточно хорошо. Имеются неопределенности в распределениях глюонов при z>0.5. (Фит A и B H1 ).

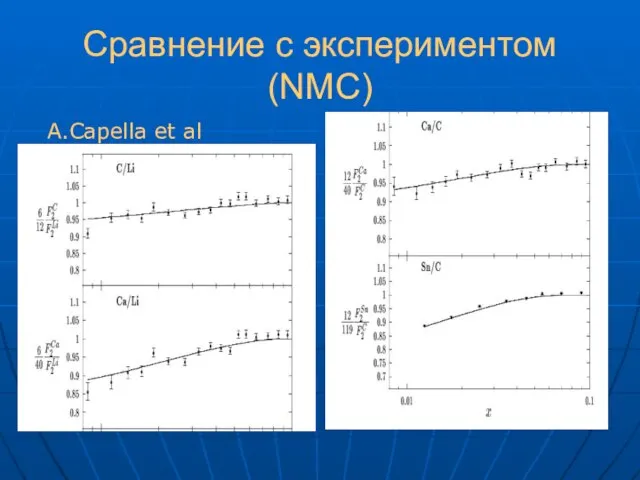
Сравнение с экспериментом (NMC)
A.Capella et al

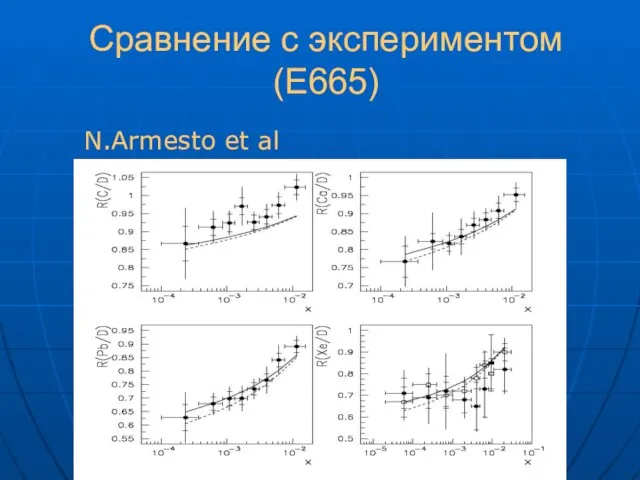
Сравнение с экспериментом (E665)
N.Armesto et al

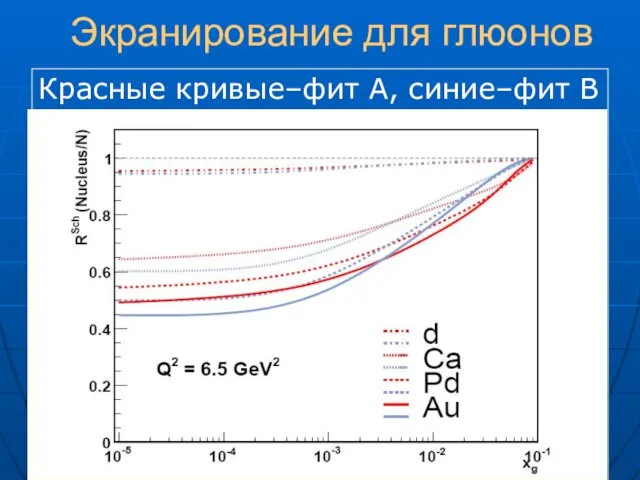
Экранирование для глюонов
Красные кривые–фит A, синие–фит B

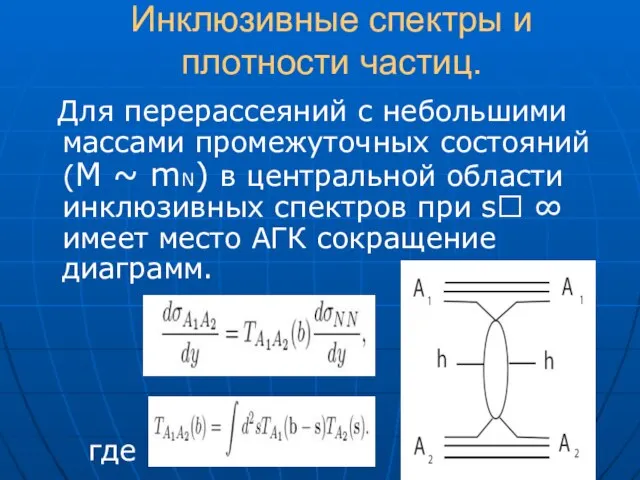
Инклюзивные спектры и плотности частиц.
Для перерассеяний с небольшими массами промежуточных состояний (М ~ mN) в центральной области инклюзивных спектров при s? ∞ имеет место АГК сокращение диаграмм.
где

Плотности частиц, рождённых в ядро - ядерных столкновениях
Для плотности числа частиц имеем
(*)
где - число NN
столкновений (тоже, что и в модели
Глаубера). Обычно ядерные эффекты RA1A2 определяются по отношению к формуле (*).

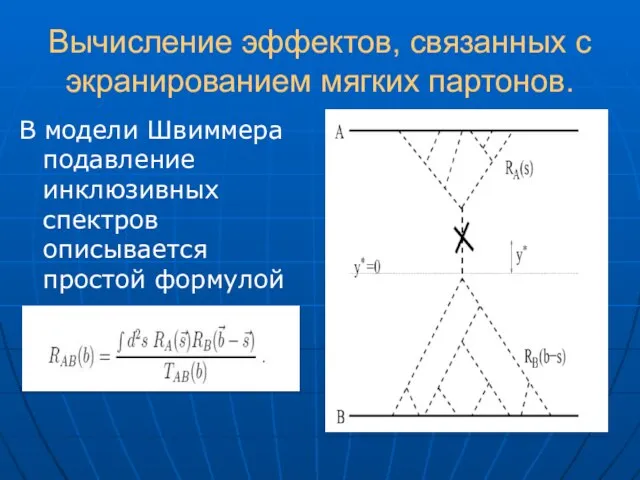
Вычисление эффектов, связанных с экранированием мягких партонов.
В модели Швиммера подавление инклюзивных спектров описывается простой формулой

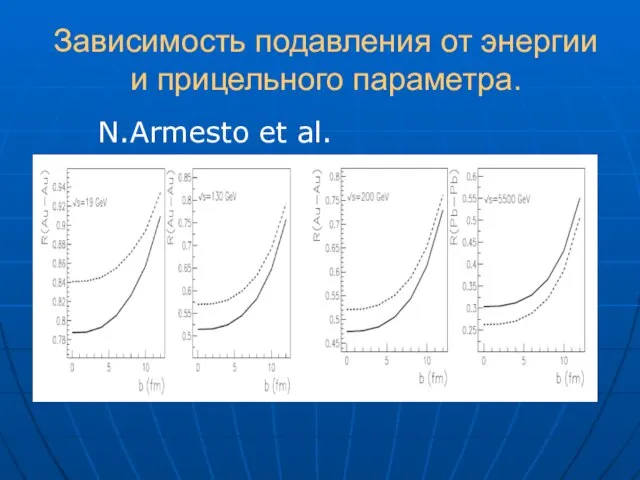
Зависимость подавления от энергии и прицельного параметра.
N.Armesto et al.

Экранирование партонов и данные RHIC.
Уменьшение плотности частиц по сравнению с моделью Глаубера согласуется с данными RHIC.
Зависимость от b
(Npart) также согласуется с эксп. данными.

Ядерные эффекты при больших pT .
В простейшей кинематике столкновения партонов Условие x << 1/mN RA накладывает при заданной энергии ограничения на величину mT.
На RHIC эффекты экранирования партонов отсутствуют в области больших pT.
Подавление рождения адронов и струй
с большими pT наблюдается на RHIC.
Это один из важнейших результатов.

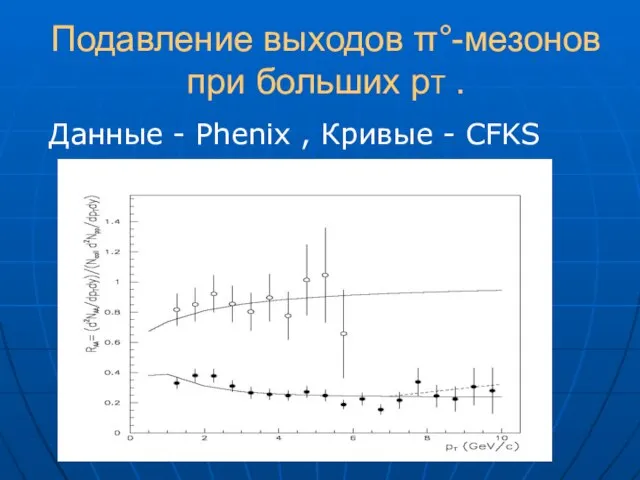
Подавление выходов π°-мезонов при больших pT .
Данные - Phenix , Кривые - CFKS

Теоретические модели для описания ядерных эффектов при больших pT .
Взаимодействия в начальном состоянии не
могут быть ответственны за эффекты
наблюдаемые на RHIC в области больших pT.
Подавление возникает за счёт взаимодействия в конечном состоянии.
Модели:
а) Когерентное излучение глюонов в веществе (аналог ЛПМ- эффекта )
R. Baier et al., B.G.Zakharov,
M. Gyulassy et al., C. Salgado et al., I.Lokhtin et al.

Теоретические модели для описания ядерных эффектов при больших pT .
б) Потери энергии в результате взаимодействия со средой ( с окружающими частицами).
Учитывается также эффект Кронина
(возрастание поперечного импульса за счёт ядерных эффектов).
A.Capella et al, A.Drees et al, W.Cassing et al
Модель хорошо описывает зависимость от b.

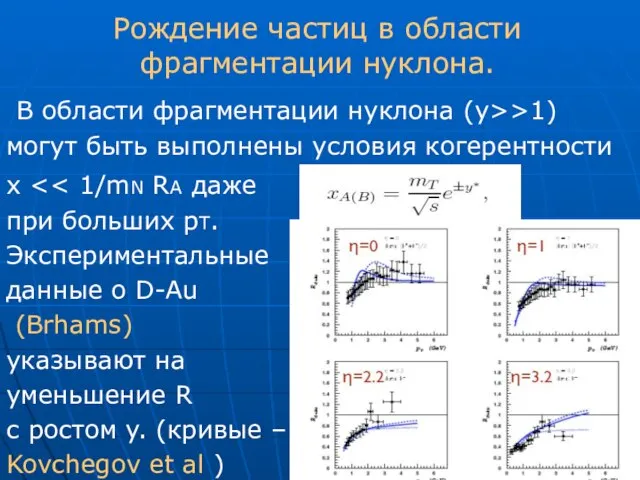
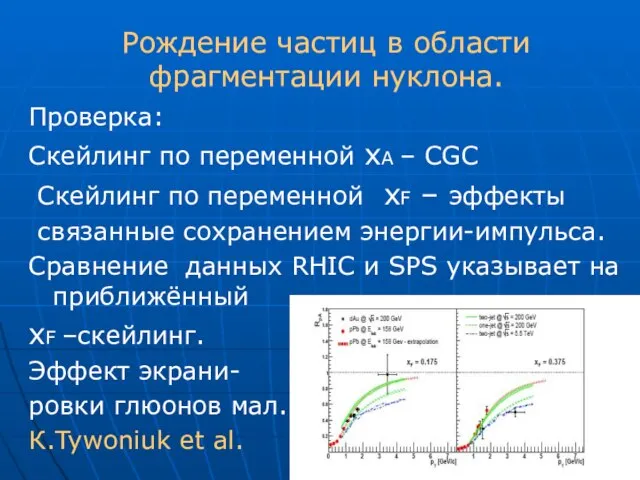
Рождение частиц в области фрагментации нуклона.
В области фрагментации нуклона (y>>1)
могут быть выполнены условия когерентности
x << 1/mN RA даже
при больших рТ.
Экспериментальные
данные о D-Au
(Brhams)
указывают на
уменьшение R
с ростом y. (кривые –
Kovchegov et al )

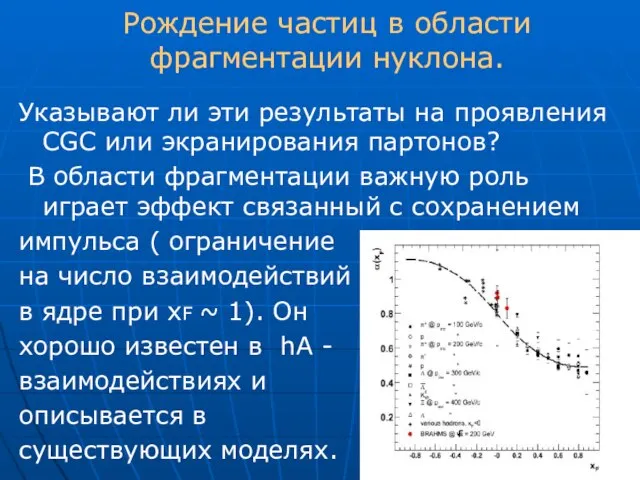
Рождение частиц в области фрагментации нуклона.
Указывают ли эти результаты на проявления CGC или экранирования партонов?
В области фрагментации важную роль играет эффект связанный с сохранением
импульса ( ограничение
на число взаимодействий
в ядре при хF ~ 1). Он
хорошо известен в hA -
взаимодействиях и
описывается в
существующих моделях.

Рождение частиц в области фрагментации нуклона.
Проверка:
Скейлинг по переменной хА – CGC
Скейлинг по переменной xF – эффекты
связанные сохранением энергии-импульса.
Сравнение данных RHIC и SPS указывает на приближённый
xF –скейлинг.
Эффект экрани-
ровки глюонов мал.
К.Tywoniuk et al.

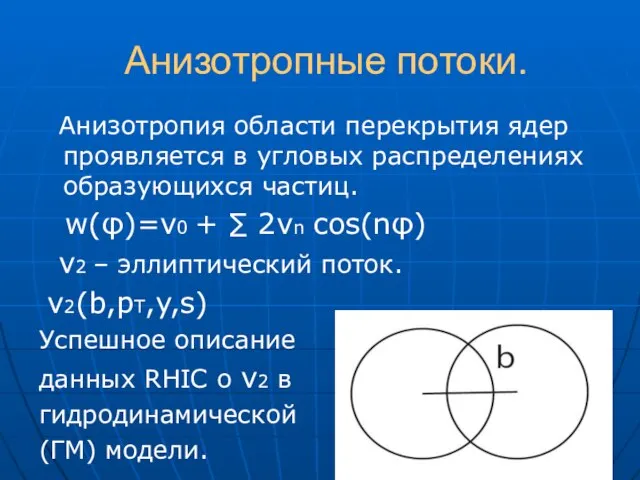
Анизотропные потоки.
Анизотропия области перекрытия ядер проявляется в угловых распределениях образующихся частиц. w(φ)=v0 + ∑ 2vn cos(nφ)
v2 – эллиптический поток.
v2(b,pT,y,s)
Успешное описание
данных RHIC о v2 в
гидродинамической
(ГМ) модели.

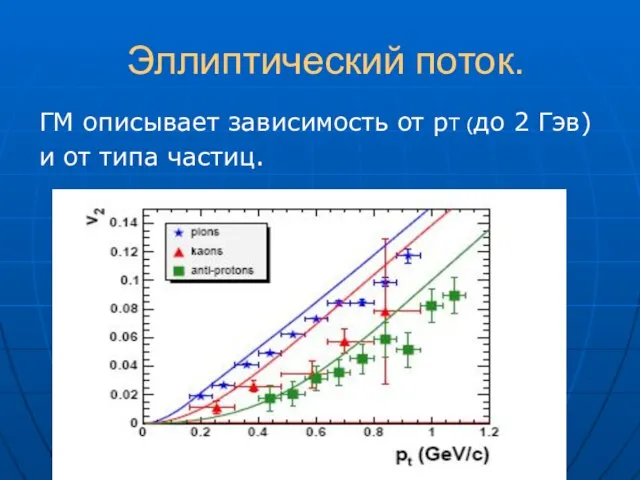
Эллиптический поток.
ГМ описывает зависимость от рТ (до 2 Гэв)
и от типа частиц.

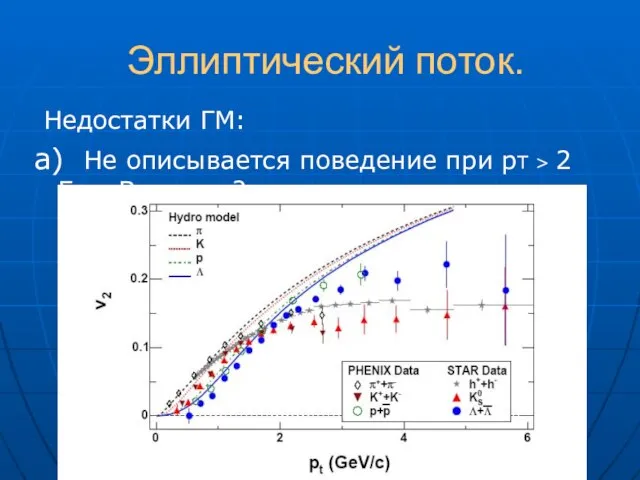
Эллиптический поток.
Недостатки ГМ:
а) Не описывается поведение при рТ > 2 Гэв. Вязкость?

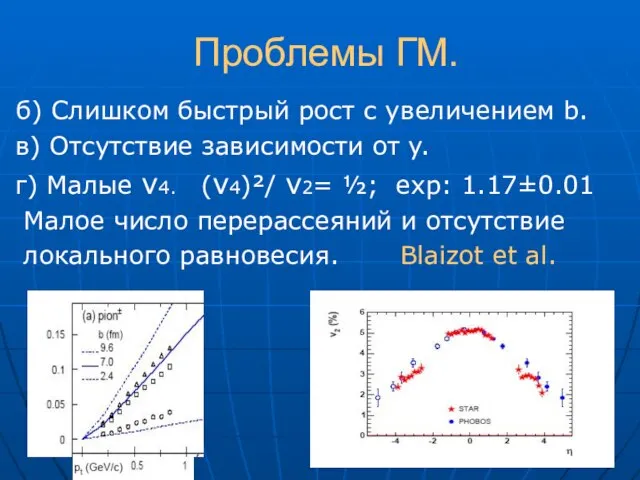
Проблемы ГМ.
б) Слишком быстрый рост с увеличением b.
в) Отсутствие зависимости от y.
г) Малые v4. (v4)²/ v2= ½; exp: 1.17±0.01
Малое число перерассеяний и отсутствие
локального равновесия. Blaizot et al.

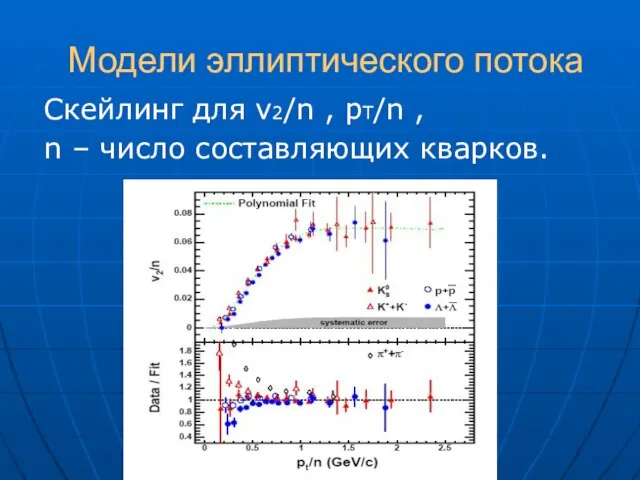
Модели эллиптического потока
Скейлинг для v2/n , pT/n ,
n – число составляющих кварков.

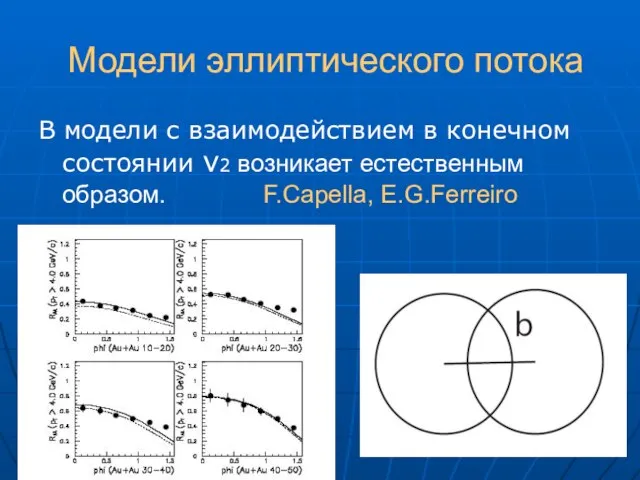
Модели эллиптического потока
В модели с взаимодействием в конечном состоянии v2 возникает естественным образом. F.Capella, E.G.Ferreiro

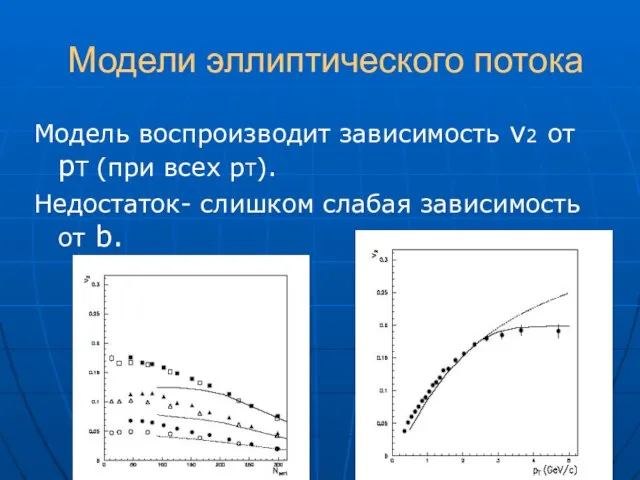
Модели эллиптического потока
Модель воспроизводит зависимость v2 от рТ (при всех рТ).
Недостаток- слишком слабая зависимость от b.

Модели эллиптического потока
Большинство моделей основано на классическом подходе. Роль квантовых эффектов? Теоретико-полевой подход показывает,
что анизотропии возникают и за счёт
распределения партонов в начальной волновой функции нуклона (ядра)
К.Г.Боресков,А.Б.К.,О.В.Канчели
Вклад в v2 дает взаимодействие не только в конечном, но и начальном состоянии!

Модели эллиптического потока

Рождение J/ψ–мезонов.
Подавление выходов тяжелых кваркониев – важная характеристика системы, рождённой в столкновениях тяжелых ионов. Для выяснения природы эффекта надо понимать динамику рождения кваркониев в NA –взаимодействиях.
Интересный результат RHIC :
при рождении J/psi в D-Au столкновениях
с xF~0 подавление J/psi существенно уменьшилось по сравнению с более низкими энергиями.
σ ~ 1 mb (σ ~ 5 mb при √s ~ 20 Гэв )

Изменение картины взаимодействия при рождении J/ψ–мезонов на RHIC.
При образования J/psi с xF=0 в NA столкновениях критическая энергия Ec находится в области энергий RHIC.
Формулы простейшей модели
Глаубера не применимы,
АГК сокращения имеют место и главный вклад в инклюзивные спектры при xF~0
дают диаграммы с взаимодействием померонов, отвечающие ядерному экранированию глюонов.

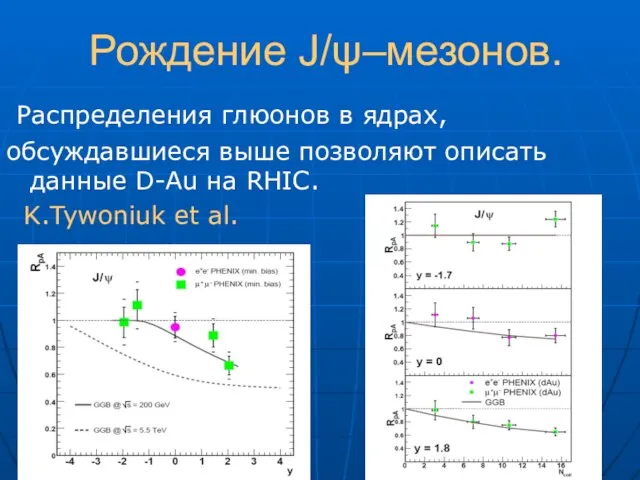
Рождение J/ψ–мезонов.
Распределения глюонов в ядрах,
обсуждавшиеся выше позволяют описать данные D-Au на RHIC.
K.Tywoniuk et al.

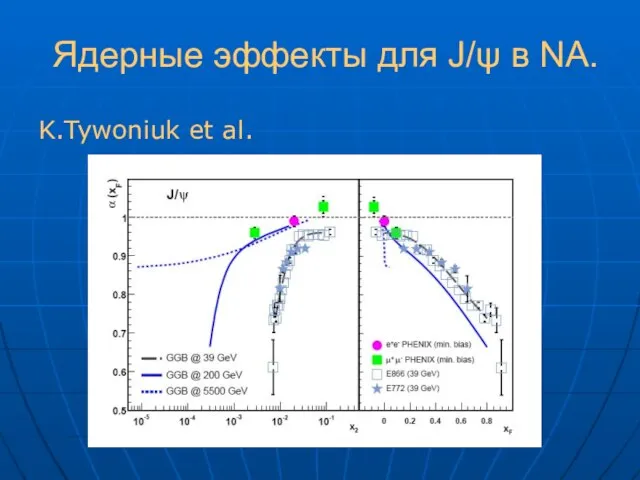
Ядерные эффекты для J/ψ в NA.
Параметризация инклюзивных сечений
Учёт изменения пространственно-временной картины позволяет описать
данные о рождении J/ψ в NA –взаимодействиях при всех энергиях и получить предсказания для LHC
(переход от xF к хА –скейлингу).

Ядерные эффекты для J/ψ в NA.
K.Tywoniuk et al.

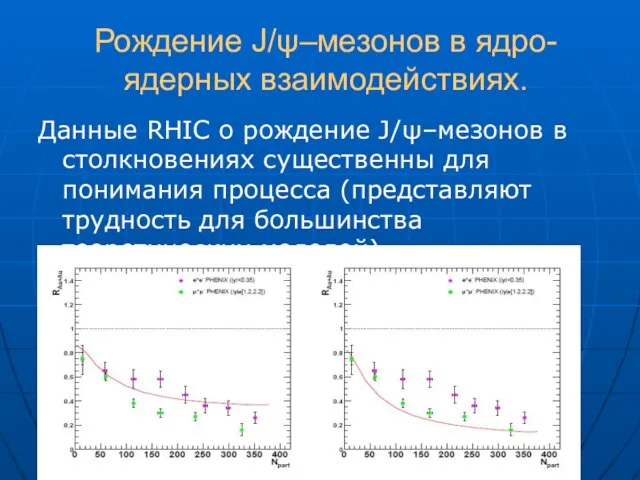
Рождение J/ψ–мезонов в ядро-ядерных взаимодействиях.
Данные RHIC о рождение J/ψ–мезонов в столкновениях существенны для понимания процесса (представляют трудность для большинства теоретических моделей).

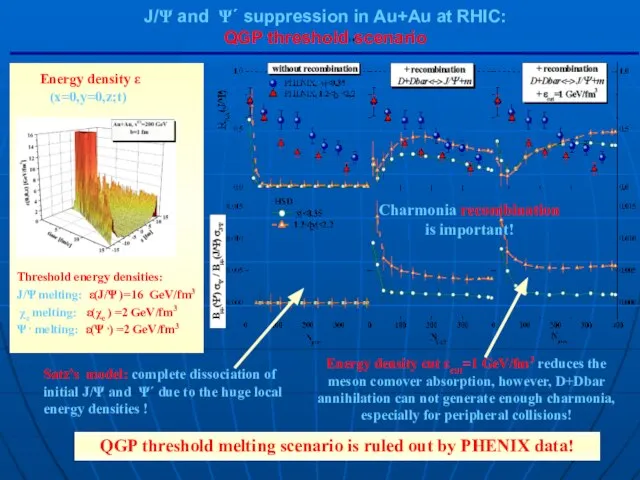
QGP threshold melting scenario is ruled out by PHENIX data!
J/Ψ and Ψ´ suppression in Au+Au at RHIC:
QGP threshold scenario
Satz’s model: complete dissociation of initial J/Ψ and Ψ´ due to the huge local energy densities !
Charmonia recombination
is important!
Energy density cut εcut=1 GeV/fm3 reduces the meson comover absorption, however, D+Dbar annihilation can not generate enough charmonia,
especially for peripheral collisions!
Energy density ε (x=0,y=0,z;t)
Threshold energy densities:
J/Ψ melting: ε(J/Ψ )=16 GeV/fm3
χc melting: ε(χc ) =2 GeV/fm3
Ψ ‚ melting: ε(Ψ ‚) =2 GeV/fm3

Модель с взаимодействием в конечном состоянии для рождения J/ψ–мезонов в ядро-ядерных взаимодействиях.
«Аномальное» подавление J/ψ–мезонов в
ядро-ядерных взаимодействиях на SPS хорошо
Описывается в модели с взаимодействием
в конечном состоянии. A.Capella et al
Для RHIC необходимо учесть изменение в поглощении J/ψ на нуклонах (см. выше) и наличие рекомбинации –мезонов в J/ψ.

Модель с взаимодействием в конечном состоянии для рождения J/ψ–мезонов в ядро - ядерных взаимодействиях.
При учёте рекомбинации
Величина С быстро растёт с увеличением энергии и при энергии √s = 200 Гэв С~1.
С учётом рекомбинации модель описывает данные о подавлении J/ψ–мезонов в ядерных взаимодействиях .

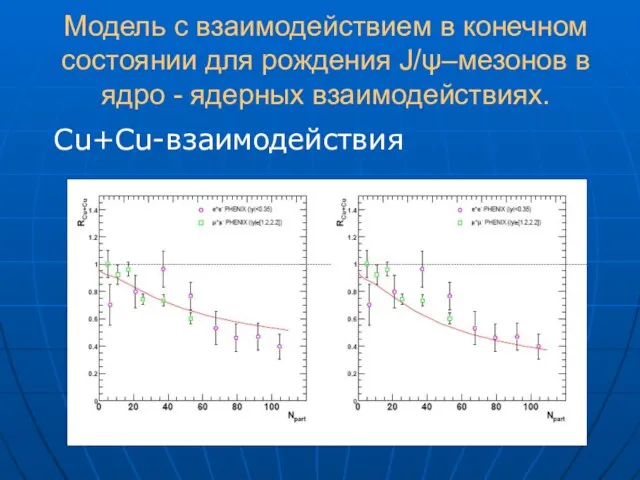
Модель с взаимодействием в конечном состоянии для рождения J/ψ–мезонов в ядро - ядерных взаимодействиях.
Cu+Cu-взаимодействия

Заключение.
Изучение ядро - ядерных взаимодействий при высоких энергиях даёт важную информацию о свойствах КХД и пространственно-временной структуре ядерных процессов.
Структурные функции ядер и распределения кварков и глюонов в ядрах при х? 0 могут быть вычислены, используя формализм Грибова.

Заключение.
Взаимодействия партонов с малыми х играют важную роль в процессах взаимодействия тяжелых ионов на
RHIC и будут ещё более существенны на LHC . Однако ”насыщение” партонных распределений на RHIC не достигнуто.
В процессах рождения частиц и струй с большими рТ в центральной области быстрот главную роль играет взаимодействие в конечном состоянии.