Содержание
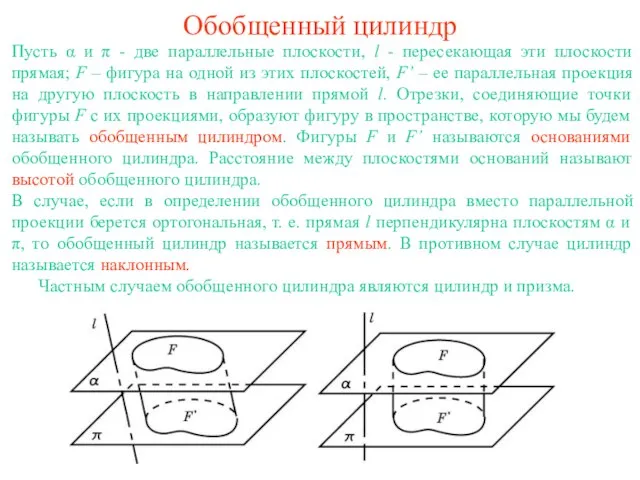
- 2. Обобщенный цилиндр Пусть α и π - две параллельные плоскости, l - пересекающая эти плоскости прямая;
- 3. Объем обобщенного цилиндра Теорема. Объем прямого обобщенного цилиндра равен произведению площади его основания на высоту. Следствие
- 4. Упражнение 1 Может ли объем фигуры в пространстве быть: а) отрицательным числом; б) нулем? Ответ: а)
- 5. Упражнение 2 Диагональ куба равна 2 см. Найдите его объем.
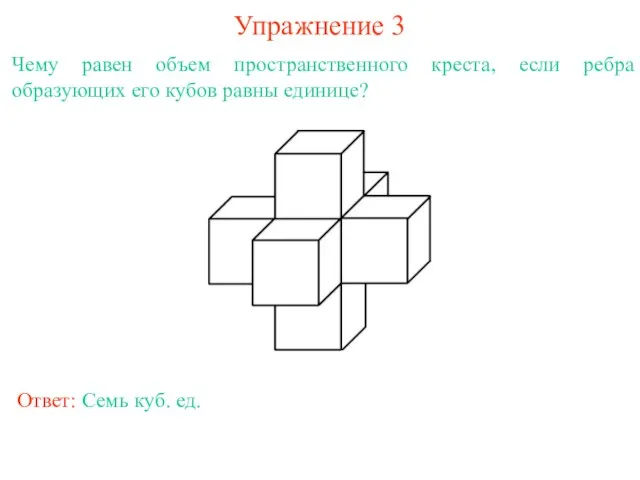
- 6. Упражнение 3 Чему равен объем пространственного креста, если ребра образующих его кубов равны единице? Ответ: Семь
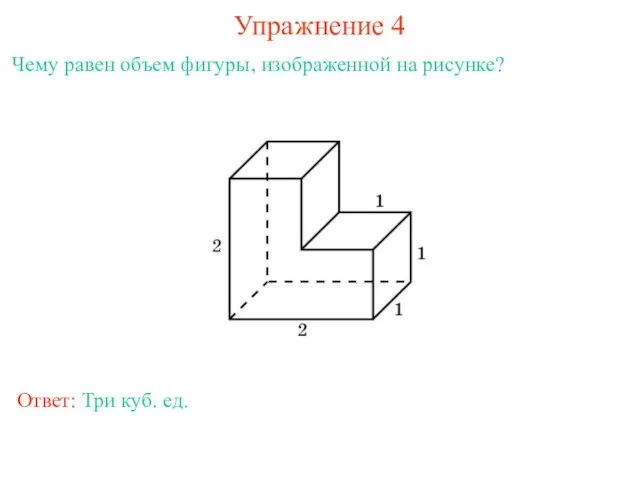
- 7. Упражнение 4 Чему равен объем фигуры, изображенной на рисунке? Ответ: Три куб. ед.
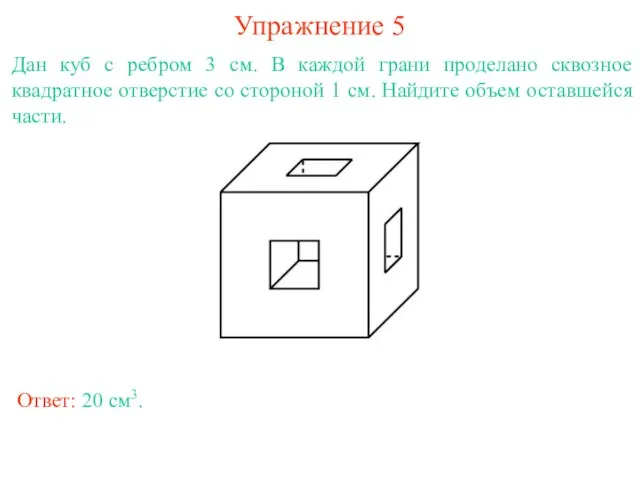
- 8. Упражнение 5 Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со
- 9. Упражнение 6 Как относятся объемы двух кубов: данного и его модели, уменьшенной в масштабе: а) 1
- 10. Упражнение 7 Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98
- 11. Упражнение 8 В прямом параллелепипеде стороны основания равны 8 см и 5 см и образуют угол
- 12. Упражнение 9 Как изменится объем прямого параллелепипеда, если: а) одно из его измерений увеличить в 2
- 13. Упражнение 10 Осевое сечение прямого кругового цилиндра - квадрат со стороной 1 см. Найдите объем цилиндра.
- 14. Упражнение 11 Одна кружка вдвое выше другой, зато другая в полтора раза шире. Какая кружка вместительнее?
- 15. Упражнение 12 Диагональ осевого сечения цилиндра равна d и наклонена к плоскости основания под углом φ.
- 16. Упражнение 13 Найдите объем фигуры, которая получается при вращении квадрата вокруг его стороны, равной a. Ответ:
- 17. Упражнение 14 Два цилиндра образованы вращением одного и того же прямоугольника около каждой из неравных его
- 18. Упражнение 15 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см,
- 19. Упражнение 16 Найдите объем правильной четырехугольной призмы, сторона основания которой 5 см и высота 8 см.
- 20. Упражнение 17 Найдите высоту правильной четырехугольной призмы, если сторона ее основания 20 см и объем 4800
- 21. Упражнение 18 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. В каком отношении
- 22. Упражнение 19 Основание прямой призмы - ромб, площадь которого равна 1 м2. Площади диагональных сечений равны
- 23. Упражнение 20 Найдите формулу объема правильной n-угольной призмы, высота которой равна h, а сторона основания равна
- 24. Упражнение 21 Объем правильной шестиугольной призмы равен V. Определите объем призмы, вершинами оснований которой являются середины
- 25. Упражнение 22 Во сколько раз объем цилиндра, описанного около правильной четырехугольной призмы, больше объема цилиндра, вписанного
- 26. Упражнение 23 В цилиндрический сосуд, диаметр которого равен 9 см, опущена деталь. При этом уровень жидкости
- 27. Упражнение 24 Через точку окружности основания прямого кругового цилиндра проведена плоскость под углом φ к этому
- 29. Скачать презентацию






















 Культура – многозначность понятия
Культура – многозначность понятия О НАС На рынке развлекательных услуг более 5 лет. Огромный опыт в проведении и оформлении различных мероприятий любого масштаба. Яр
О НАС На рынке развлекательных услуг более 5 лет. Огромный опыт в проведении и оформлении различных мероприятий любого масштаба. Яр Психогигиена – система специальных мероприятий, имеющих задачей сохранение и укрепление психического здоровья человека
Психогигиена – система специальных мероприятий, имеющих задачей сохранение и укрепление психического здоровья человека Орлеанская дева
Орлеанская дева Законы термодинамики
Законы термодинамики Вербное воскресение
Вербное воскресение Обращения
Обращения Международные и национальные стандарты в области свободы выражения мнений и доступа к информации Вячеслав Абрамов, Международный
Международные и национальные стандарты в области свободы выражения мнений и доступа к информации Вячеслав Абрамов, Международный «Будущее социально ответственного инвестирования в России: результаты совместного проекта Московской школы Управления СКОЛКОВО
«Будущее социально ответственного инвестирования в России: результаты совместного проекта Московской школы Управления СКОЛКОВО  Если Ваши права нарушены
Если Ваши права нарушены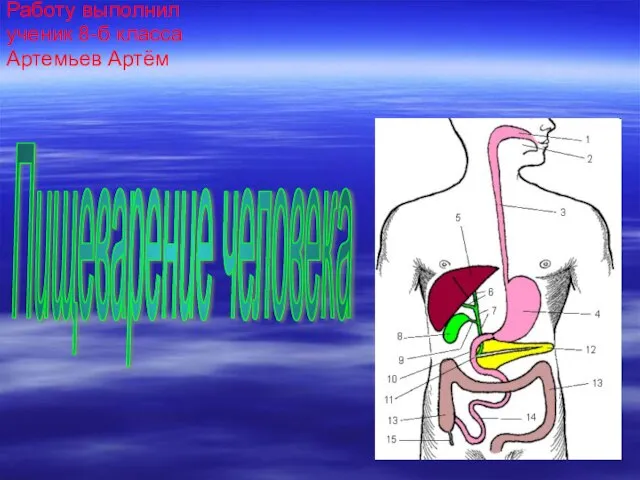 Пищеварение человека
Пищеварение человека Давление в неподвижных жидкостях и газах
Давление в неподвижных жидкостях и газах Теория Вечной Вселенной
Теория Вечной Вселенной Сила Внимания
Сила Внимания Старт карьеры-2009
Старт карьеры-2009 Организационное поведение. Восприятие
Организационное поведение. Восприятие Участок резки матов на карты
Участок резки матов на карты Электронный процессор Excel
Электронный процессор Excel Православное учение о человеке (4 класс)
Православное учение о человеке (4 класс) Структура межпланетных магнитных полей и солнечная активность
Структура межпланетных магнитных полей и солнечная активность "Мы тоже имеем права!"
"Мы тоже имеем права!" Оповещение о камнепадах и паводковых волнах в Норвегии
Оповещение о камнепадах и паводковых волнах в Норвегии Бичурин Никита Яковлевич
Бичурин Никита Яковлевич ARTE LAMP_магнитные системы
ARTE LAMP_магнитные системы Её величествомода
Её величествомода Ruby on Rails
Ruby on Rails Молодость в креме вместо инъекции
Молодость в креме вместо инъекции Выездной ресторан Заводной апельсин
Выездной ресторан Заводной апельсин