Содержание
Слайд 21. Высота конуса равна 8 см. На каком расстоянии от вершины конуса
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса
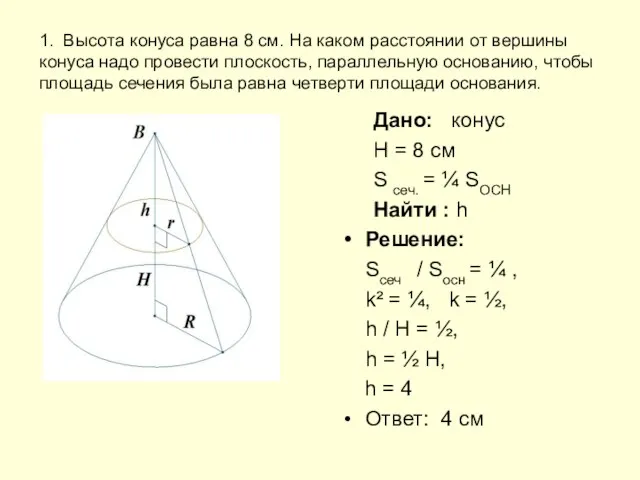
надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна четверти площади основания.
Дано: конус
H = 8 см
S сеч. = ¼ SOCH
Найти : h
Решение:
Sсеч / Sосн = ¼ ,
k² = ¼, k = ½,
h / H = ½,
h = ½ Н,
h = 4
Ответ: 4 см
Слайд 3Дано: Конус вписан в пирамиду
Объем конуса равен V
Найти: объем пирамиды
Дано: Конус вписан в пирамиду
Объем конуса равен V
Найти: объем пирамиды
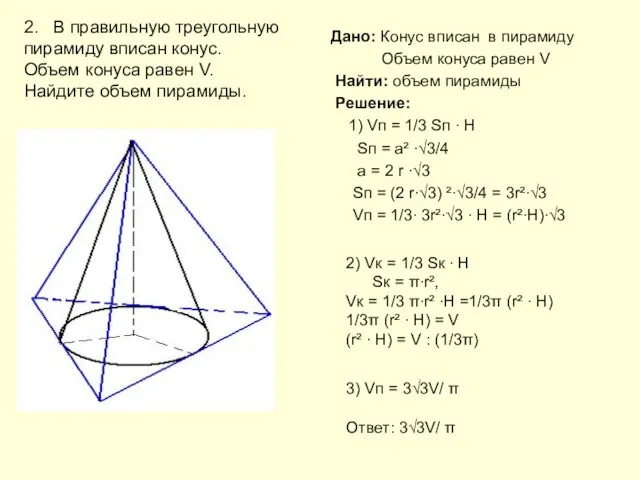
Решение:
1) Vп = 1/3 Sп ∙ H
Sп = а² ∙√3/4
а = 2 r ∙√3
Sп = (2 r∙√3) ²∙√3/4 = 3r²∙√3
Vп = 1/3∙ 3r²∙√3 ∙ H = (r²∙H)∙√3
1) Vп = 1/3 Sп ∙ H
Sп = а² ∙√3/4
а = 2 r ∙√3
Sп = (2 r∙√3) ²∙√3/4 = 3r²∙√3
Vп = 1/3∙ 3r²∙√3 ∙ H = (r²∙H)∙√3
2. В правильную треугольную пирамиду вписан конус. Объем конуса равен V. Найдите объем пирамиды.
2) Vк = 1/3 Sк ∙ H
Sк = π∙r²,
Vк = 1/3 π∙r² ∙H =1/3π (r² ∙ Н)
1/3π (r² ∙ Н) = V
(r² ∙ Н) = V : (1/3π)
3) Vп = 3√3V/ π
Ответ: 3√3V/ π
- Предыдущая
Определение графа История создания сети интернет
История создания сети интернет Презентация на тему Русская армия в 18 веке и её великие полководцы
Презентация на тему Русская армия в 18 веке и её великие полководцы Предпринимательство и его организационные формы. Тема 14
Предпринимательство и его организационные формы. Тема 14 Презентация на тему Международные экономические организации Международные правительственные (межгосударственные) экономически
Презентация на тему Международные экономические организации Международные правительственные (межгосударственные) экономически Овощной салат с зелёным чаем
Овощной салат с зелёным чаем Липецкий зоопарк
Липецкий зоопарк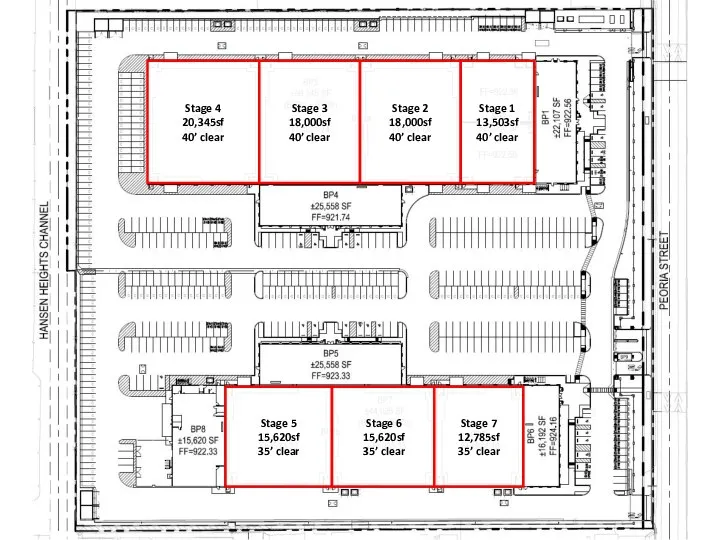 Sun Valley Site Plan Mock Up
Sun Valley Site Plan Mock Up OET-12
OET-12 Отношение студентов ТМК к занятиям спортом в учебное время
Отношение студентов ТМК к занятиям спортом в учебное время Здоровьесберегающие технологии в начальной школе
Здоровьесберегающие технологии в начальной школе Фоносемантический анализ предложения
Фоносемантический анализ предложения Повышение эффективности использования машиннотракторного агрегата для поверхностной обработки
Повышение эффективности использования машиннотракторного агрегата для поверхностной обработки Региональные налоги РФ
Региональные налоги РФ Психология, педагогика және мәдениет факультеті
Психология, педагогика және мәдениет факультеті Создание макета русской деревни в рамках предмета «Технология»
Создание макета русской деревни в рамках предмета «Технология» Единый недвижимый комплекс
Единый недвижимый комплекс Судейский семинар национальной категории по дисциплинам спидскейтинга
Судейский семинар национальной категории по дисциплинам спидскейтинга SFM-285 СПМ200-6843080 “Набивка подушки”. Форма заливочная. Концепт разъема
SFM-285 СПМ200-6843080 “Набивка подушки”. Форма заливочная. Концепт разъема 2022-04-04_GIA-9_normat_dok
2022-04-04_GIA-9_normat_dok Способы формирования познавательного интереса, как необходимого условия повышения качества знаний учащихся
Способы формирования познавательного интереса, как необходимого условия повышения качества знаний учащихся Презентация на тему Агроклиматические ресурсы
Презентация на тему Агроклиматические ресурсы  Підвищення кваліфікації вчителів за напрямом інформатика
Підвищення кваліфікації вчителів за напрямом інформатика Надзвичайні ситуації та їх запобігання
Надзвичайні ситуації та їх запобігання Жизненный и творческий путь Александра Блока
Жизненный и творческий путь Александра Блока Ораторское искусство
Ораторское искусство Айфоны X, XR и XS MAX
Айфоны X, XR и XS MAX ЕГЭ ПО РУССКОМУ ЯЗЫКУ2011
ЕГЭ ПО РУССКОМУ ЯЗЫКУ2011 Проектная работа «Кулинарная книга 1 – В класса».
Проектная работа «Кулинарная книга 1 – В класса».