Объем тела

Цели урока:
Ввести понятие объема тел, его свойств, единиц измерения объёма.
Повторить с учащимися формулы для нахождения объёма параллелепипеда, куба.
Познакомить учащихся с объёмами прямой призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями.

Подобно тому как все искусства
тяготеют к музыке,
все науки
стремятся к математике. Д. Сантаяна

Геометрия есть искусство правильно рассуждать на неправильных чертежах.
Пойа Д.

Площадь
Площадь многоугольника- это положительная величина той части плоскости , которую занимает многоугольник.
Объем
Объем тела – это положительная величина той части пространства , которую занимает геометрическое тело.

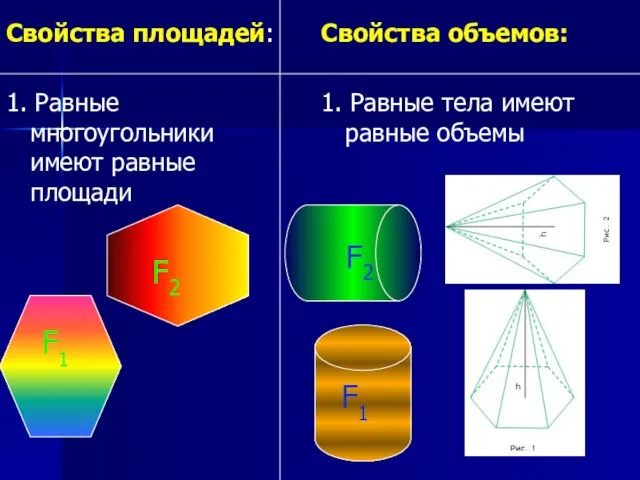
Свойства площадей:
1. Равные многоугольники имеют равные площади
Свойства объемов:
1. Равные тела имеют равные объемы
F1
F2
F1
F2

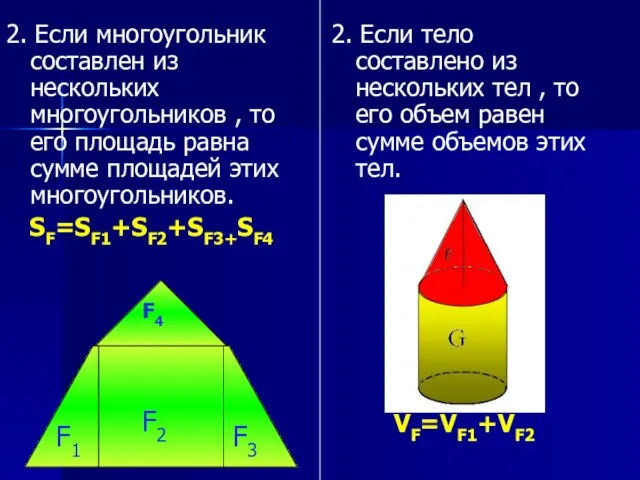
2. Если многоугольник составлен из нескольких многоугольников , то его площадь равна сумме площадей этих многоугольников.
SF=SF1+SF2+SF3+SF4
2. Если тело составлено из нескольких тел , то его объем равен сумме объемов этих тел.
VF=VF1+VF2

Площадь
За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков.
1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2 , 1 а, 1 га и т.д.
Объем
За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков.
Куб с ребром 1 см называют кубическим сантиметром и обозначают см3.
Аналогично определяют
1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д.
1
1
1
1
1

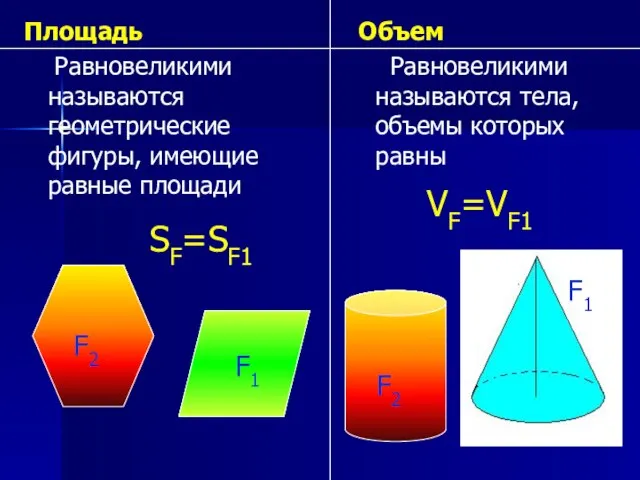
Площадь
Равновеликими называются геометрические фигуры, имеющие равные площади
Объем
Равновеликими называются тела, объемы которых равны
VF=VF1
F2
F1
F2
F1
SF=SF1

В стереометрии рассматриваются объемы многогранников и объемы тел вращения.

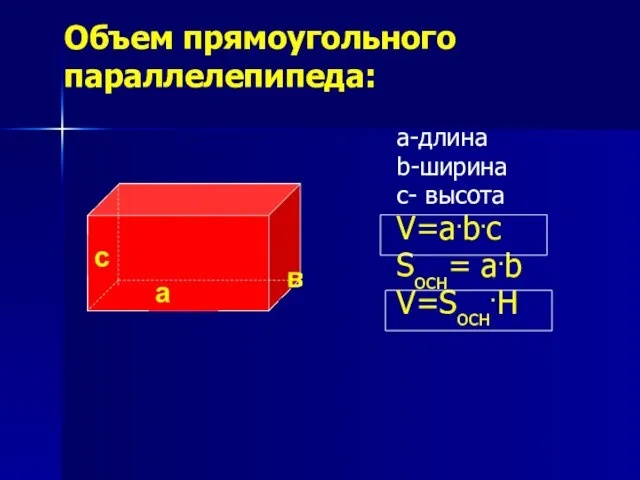
Объем прямоугольного параллелепипеда:
а-длина
b-ширина
с- высота
V=a.b.c
Sосн= a.b
V=Sосн.H

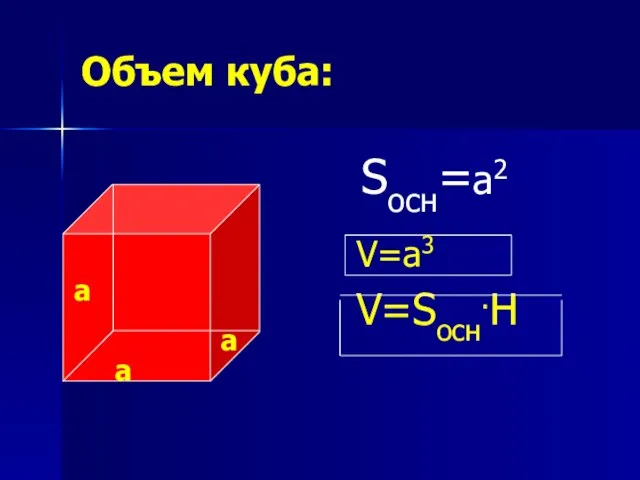
Объем куба:
V=a3
V=Sосн.H
Sосн=a2

Объем прямой призмы:
V=Sосн.H
Vпарал=Sосн.H
S осн=2.SABC
По свойству объемов
Vпарал= 2.SABС.H
V призмы = (V парал) :2
V призмы = (2.SABС. H): 2

Объем пирамиды:
У 2 и 3 пирамиды- SC- общая,
тр CC1B1= тр CBB1
У 1 и 3 пирамиды- СS- общая,
тр SAB= тр BB1S
V1=V2=V3
V призмы= 3 V пирам
Vпирамиды=1 V призмы
3
Vпирамиды=1 Sосн .H
3
Достроим пирамиду
ABCS до призмы. Достроенная
призма будет состоять из 3
пирамид- SABC, SCC1B1, SCBB1

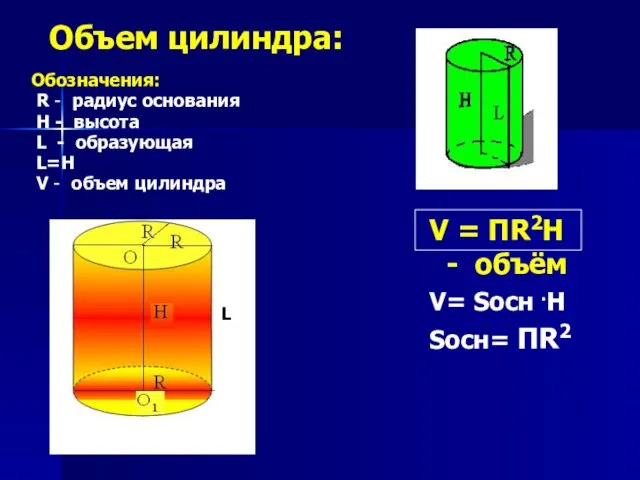
Объем цилиндра:
Обозначения:
R - радиус основания
H - высота L - образующая
L=H
V - объем цилиндра
V = ПR2H - объём
V= Sосн .H
Sосн= ПR2

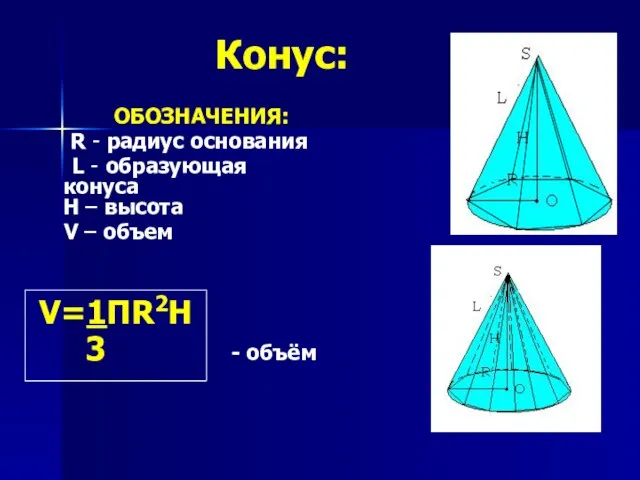
Конус:
ОБОЗНАЧЕНИЯ:
R - радиус основания
L - образующая конуса
H – высота
V – объем
V=1ПR2Н
3 - объём

Это интересно:

Проверь свои знания:
Сформулируйте понятие объема.
Сформулируйте основные свойства объемов тел.
Назовите единицы измерения объема тел.
Назовите формулу для измерения объема
- прямоугольного параллелепипеда;
- объема куба;
- объем прямой призмы;
- объем пирамиды;
- объем цилиндра и объем конуса.
Изменится ли объем цилиндра, если радиус его основания увеличить в 2 раза, а высоту уменьшить в 4 раза?
V = ПR2H V=П(2R)2 .H =П4R2. H =ПR2. H
4 4
Основаниями двух пирамид с равными высотами являются четырехугольники с соответственно равными сторонами. Равны ли объемы этих пирамид?
Из каких тел состоит тело, полученное вращением равнобедренной трапеции вокруг большего основания?

Домашняя работа:
Выучить формулы объемов тел, определения.
№ 648(а,в), № 685, № 666(а,в)

Закрепление пройденного материала:
Задача №1
Три латунных куба с ребрами 3см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?
+ + =

Решение:
VF=VF1+VF2 +VF3
VF1=33 =27 (см3)
VF2=43 =64 (см3)
VF3=53 =125 (см3)
VF=27+64 +125=216 (см3)
VF=а3
а3=216 (см3)
а= 6 (см)
Ответ: ребро куба равно 6 см.

Задача №2
Найдите объем правильной четырехугольной пирамиды, высота которой равна 12 см, а сторона основания 13 см.

Решение:
V=1 Sосн . H
3
ABCD- квадрат
S ABCD=a2
S ABCD= 132=169
V=1 169 . 12 =676 (см3)
3
Ответ : Объем правильной четырехугольной пирамиды равен 676 см3

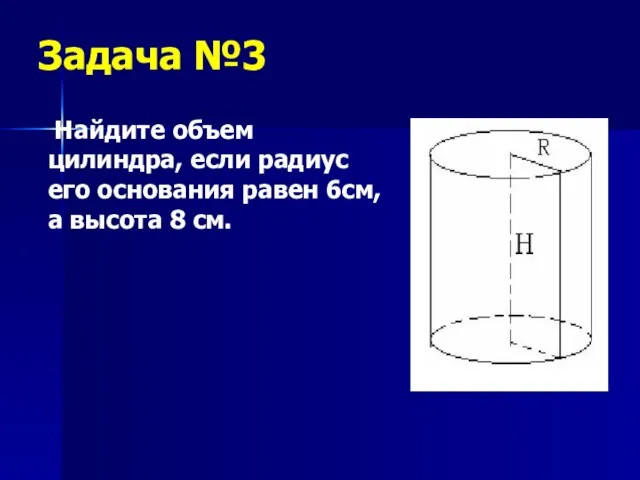
Задача №3
Найдите объем цилиндра, если радиус его основания равен 6см, а высота 8 см.

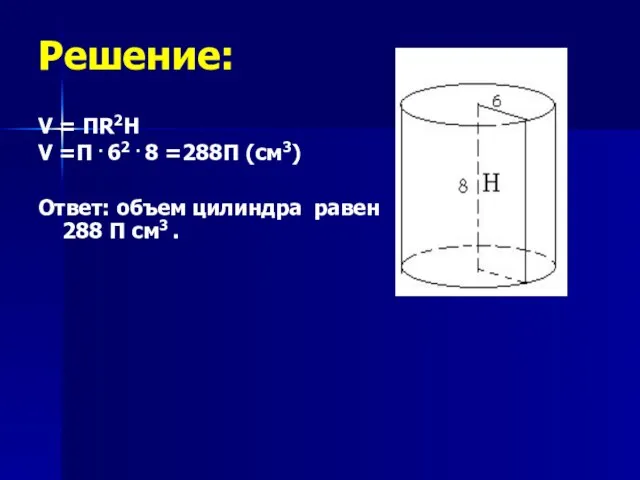
Решение:
V = ПR2H
V =П . 62 . 8 =288П (см3)
Ответ: объем цилиндра равен 288 П см3 .

Все рисунки и чертежи выполнены автором данной работы- Варенко Оксаной Валентиновной в программах: Microsoft Office Word, Paint.
В данной работе использованы фотографиии c сайтов:
1) 1) http://geology.com/satellite/l…Конус_выноса
2) 2) http://www.ehow.com/info_80187…-конус нарастания
http://www.rakushki.com/catalo…- конус морские моллюски
http://www.astronet.ru/db/msg/…- Телесный_угол