Содержание
- 2. Историческая страница
- 3. Число – арифмос (греч.) Геометрия – гео – земля (греч.), метрео – меряю (греч.) Аль джебр
- 4. Евклид. «Начала». Издание 1482 г.
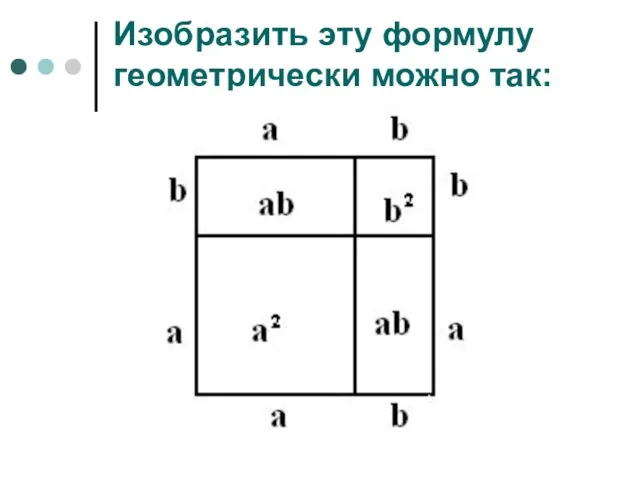
- 5. Евклид. «Начала». «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке,
- 6. Изобразить эту формулу геометрически можно так:
- 7. Три способа формулировки математических утверждений: Словесный – понятный, но длинный, неудобный; Геометрический – наглядный, но не
- 8. Аль джебр – восстановление (арабск.) algebr
- 9. Тренировочные упражнения
- 10. Составьте по описанию алгебраические выражения: Сумма квадратов чисел а и b. Разность между числом m и
- 11. Запишите в виде степени выражения:
- 12. Найдите неизвестное х: (24)х = 212; 10х = 10000; 53 ⋅ 54 = 52 + х;
- 13. Заполните пропуски в формулах: (а +…)2 = … + 2аb + … ; (а … b)…
- 14. Расширение знаний по формулам сокращенного умножения
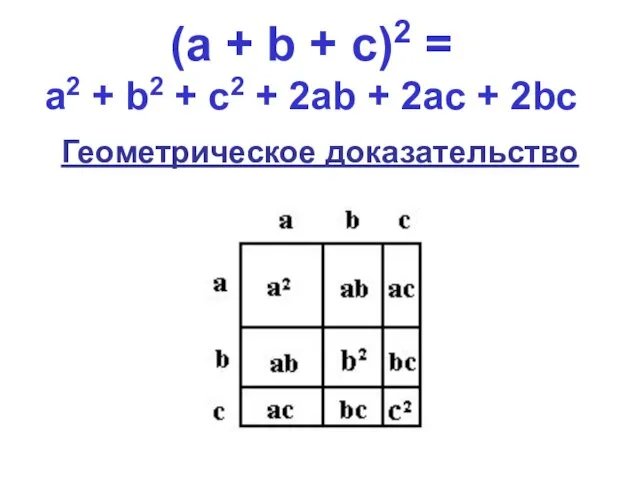
- 15. (а + b + с)2 = а2 + b2 + с2 + 2аb + 2ас +
- 16. Найдите квадрат выражения: а) (а – х + у)2 б) (а – b – с)2
- 17. Треугольник Паскаля
- 18. Блез Паскаль (1623 – 1662)
- 19. Рассмотрим двучлены: (а + b)0 = 1 (a + b)1 = a + b (a +
- 20. Составим таблицу из их коэффициентов: 1 1 1 1 2 1 1 3 3 1
- 21. Закон образования коэффициентов 1 - 20 1 1 - 21 1 2 1 - 22 1
- 22. Вариации числа 100
- 23. Рассмотрим комбинации числа 100:
- 24. Изменив положение одной цифры, добейтесь, чтобы равенство 102 = 100 было верным.
- 25. Примеры вариантов некоторых формул: a2 + b2 = (a + b)2 – 2ab a2 + b2
- 26. Вычисление квадрата числа
- 27. a2 = а2 – b2 + b2 = (a – b)(a + b) + b2, где
- 28. Вычислите: 1) 1952 2) 4882
- 29. Математический софизм
- 30. Докажем, что 4 = 5.
- 31. Домашнее задание 1. Обратите внимание на пирамиды чисел: а) 1 ⋅ 8 + 1 = 9,
- 32. …Мне мудрость не чужда была земная, Разгадки тайн ища, не ведал сна я. За семьдесят перевалило
- 34. Скачать презентацию












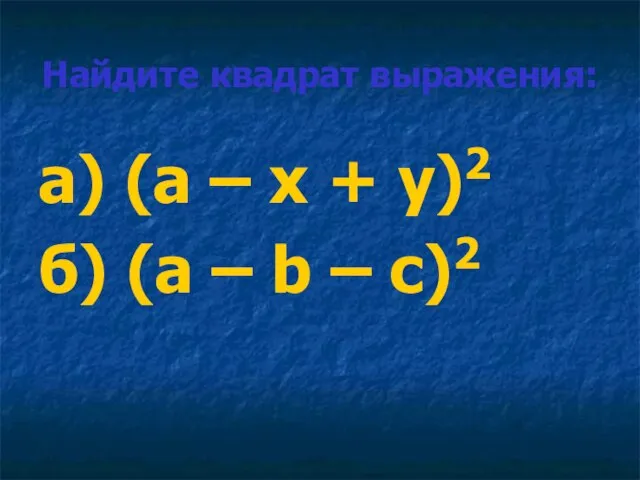
















 Алгоритм презентации на защиту
Алгоритм презентации на защиту Современная киноиндустрия
Современная киноиндустрия Кто придумал ноль ?
Кто придумал ноль ? Направления деятельности изостудии Росинка
Направления деятельности изостудии Росинка Объединение Мир искусства. Часть 3
Объединение Мир искусства. Часть 3 Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок
Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок es-Persona индивидуальные заказы
es-Persona индивидуальные заказы Основы графической грамоты. Трудовое обучение
Основы графической грамоты. Трудовое обучение Установка разделения изотопов бора методом экстрактивной ректификации
Установка разделения изотопов бора методом экстрактивной ректификации Оценка уровня развития базовых способностей обучающихся
Оценка уровня развития базовых способностей обучающихся Презентация на тему Занятие по профориентации «Профессия - ветеринар»
Презентация на тему Занятие по профориентации «Профессия - ветеринар» История про маленьких лягушат….
История про маленьких лягушат…. Очистка и дезинфекция медицинских инструментов.
Очистка и дезинфекция медицинских инструментов. Особенности кредитно-модульной организации учебного процесса
Особенности кредитно-модульной организации учебного процесса Современные PLC телекоммуникации
Современные PLC телекоммуникации Здоровьесберегающие образовательные технологии на уроках английского языка
Здоровьесберегающие образовательные технологии на уроках английского языка Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г.
Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г. «Стабильный успех»
«Стабильный успех» Технологические среды в микроэлектронике. Газоподготовка в электронной технике
Технологические среды в микроэлектронике. Газоподготовка в электронной технике Я через 15 лет
Я через 15 лет The Golden Age
The Golden Age Машинные швы
Машинные швы РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года.
РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года. Криптосистемы с открытым ключем
Криптосистемы с открытым ключем Экскурсия в город Мастеров и Мастериц
Экскурсия в город Мастеров и Мастериц Битва за Днепр
Битва за Днепр Насилие в произведениях искусства
Насилие в произведениях искусства Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх
Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх